 |
|
Приклад розв’язання завдання 1.
Виконати дії з матрицями: 3А+2А; А*В; В*А; А*С;
де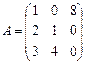 
Розв’язання:
а)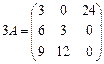 
; 
.
.
б)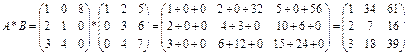 
отже А*В¹В*А, тобто матриці А та В не комутативні.
в) 
.
Обчислити визначник матриці А.
Розв’язання: Обчислимо визначник за допомогою алгебраїчних доповнень.
.
3. Знайти матрицю А-1, обернену до матриці А
Розв’язання: Для знаходження оберненої матриці використаємо формулу:
,
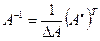де А· - приєднана до А матриця, складена з алгебраїчних доповнень елементів матриці А, символ Т позначає операцію транспортування.
а) 
,
отже, матриця А невироджена, тобто, вона має обернену.
б) Обчислимо алгебраїчні доповнення елементів матриці А:
, 
, 
,
, 
, 
, 
, 
.
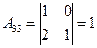Тоді,
.
Отже
в) Отримаємо обернену матрицю
г) Впевнимось, що А-1 – обернена матриця до А.
Таким чином, матриця 
є оберненою до матриці А.
4. Розв’язати матричне рівняння A*X=B.
Розв’язання: Помножимо обидві частини рівняння А*Х=В на А-1 зліва
тобто
А-1А*Х=А-1*В, або Х=А-1*В.
Таким чином, для розв’язку задачі необхідно побудувати матрицю А-1 обернену до матриці А.
З попередньої задачі маємо
.
Тоді розв’язком матричного рівняння буде матриця:
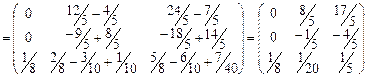
5. Розв’язати систему рівнянь
а) Методом Крамера
Розв’язання:
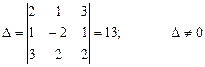
Тоді:
б) Методом Гаусса
Розв’язання:
Складемо розширену матрицю системи та приведемо її до трикутної за допомогою елементарних перетворень.
А= 
.
Від другого рядка матриці віднімемо перший рядок помножений на 2, а від третього рядка віднімемо перший помножений на 3:
.
Від третього рядка віднімемо другий помножений на 8:
.
Відповідно запишемо систему:
З другого рівняння системи маємо:
,
а з першого рівняння:
.
Отже, розв’язок системи
.
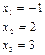в) матричним методом
Розв’язання:
Систему можна записати у матричному вигляді 
, де
, 
, 
.
Тоді (якщо 
) розв’язок системи знаходимо за формулою 
.
Знайдемо матрицю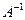 
, обернену до 
.
,
,
.
Тоді 
.
Таким чином, розв’язок системи 
.