Главная | Обратная связь

Задача о проведении касательной к кривой

Задачи, приводящие к понятию производной

Задача о вычислении скорости движущейся точки

Рассмотрим прямолинейное неравномерное движение некоторой материальной точки M. Расстояние S, на которое переместится точка M от начального положения 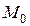за промежуток времени t, будет являться функцией времени Пусть в некоторый момент t точка M находилась на расстоянии S, а в некоторый следующий момент точка M находилась на расстоянии от начального положения 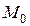. Таким образом, за величину времени 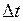величина S получила приращение Отношение дает среднюю скорость движения точки M за время Δt. Средняя скорость зависит от промежутка времени Δt и не может дать нам правильное представление об истинной скорости движения точки в момент t. Для более точного представления об истинной скорости движения в момент времени t необходимо взять как можно меньший промежуток времени Δt. Наиболее полно характеризует скорость движения точки в момент времени t тот предел, к которому стремится средняя скорость при Этот предел называют скоростью движения в данный момент:

(1)

 

Таким образом, скоростью движения в данный момент называется предел отношения приращения пути ΔS к приращению времени Δt, когда приращение времени Δt стремится к нулю.

Учитывая, что равенство (1) запишем в виде:

 

(2)

 

Это и будет скорость неравномерного движения.

 

Задача о проведении касательной к кривой

Пусть дана кривая К и на ней точка М (рис. 1). Возьмем на кривой ещё какую-нибудь точку и проведем секущую Когда точка будет перемещаться вдоль кривой, эта секущая будет вращаться вокруг точки M.

О п р е д е л е н и е. Касательной к кривой К в точке М называется предельное положение МТ секущей , когда точка вдоль по кривой стремится к совпадению с M.

Для определения положения касательной к кривой в точке М достаточно знать угловой коэффициент касательной в точке M. Для любой кривой с уравнением угловой коэффициент устанавливается следующим образом. Приращению абсциссы Δx отвечает приращение Δy ординаты. Отношение выражает угловой коэффициент секущей tgφ. Угловой коэффициент k = tgα касательной в точке M получается путем перехода к пределу при Δx → 0:

 

(3)

 

Таким образом, угловой коэффициент касательной к кривой выражается как предел отношения приращения ординаты точки Δy к приращению абсциссы точки Δx, когда приращение абсциссы Δx стремится к нулю.