Производные высших порядков

Если функция имеет конечную производную на некотором числовом промежутке, так что эта производная представляет новую функцию от x, то может оказаться что эта функция в свою очередь имеет производную. Её называют производной второго порядка или второй производной функции и обозначают одним из символов:

В п. 2 мы говорили, что скорость движения точки v равна производной от пройденного пути по времени t , а ускорение есть производная от скорости по времени. Значит, ускорение является второй производной от пути по времени t.

Подобным образом от второй производной можно перейти к третьей, четвертой производной.

О п р е д е л е н и е. Производной n-го порядка или n-ой производной от функции называется производная (первого порядка) от производной (n-1)-го порядка и обозначается в виде:

Порядок производной берётся в скобки для того, чтобы его нельзя было принять за показатель степени. Производные четвертого, пятого и высших порядков обозначаются так же с помощью римских цифр без скобок.

П р и м е р 8. Найти производную шестого порядка от функции

Решение.

Если то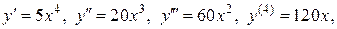

П р и м е р 9. Найти производную второго порядка от функции

Решение.

П р и м е р 10. Найти третью производную функции

Решение.

Производная второго порядка от функции, заданной в параметрическом виде находится по формуле:

(11)

П р и м е р 11. Найти вторую производную от функции , заданной параметрическими уравнениями

Решение.

Сначала найдем первую производную по правилу дифференцирования функции, заданной параметрически (формула 10) Затем по формуле (11), имеем:

Дифференциал

Пусть функция является дифференцируемой на некотором промежутке. По определению производной (формула 7) Следовательно, отношение при Δx → 0 отличается от производной на величину бесконечно малую: , где при . Умножая все члены полученного равенства на Δx , получим .

Таким образом, приращение Δy функции состоит из двух слагаемых, первое из которых есть (при f ´(x) ≠ 0) главная часть приращения, линейная относительно Δx. Произведение f ´(x)·Δx называют дифференциалом функции и обозначают через dy или df(x).

О п р е д е л е н и е. Дифференциалом функции в точке х называется главная часть ее приращения равная произведению производной функции на приращение аргумента:

(12)

Дифференциал dx независимой переменной x совпадает с приращением Δx, поэтому формулу (12) можно записать так:

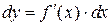
(13)

Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Рассмотрим на графике функции некоторую точку М(x,y) (рис.2), проведем в этой точке касательную к кривой и обозначим через α угол, который образует касательная с положительным направлением оси Ox.

Дадим независимой переменной приращение Δx, тогда функция получит приращение Δy. На кривой это точка 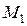. На чертеже отметим точки Т и N, 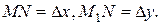Из прямоугольного треугольника MNT, имеем: Согласно геометрическому смыслу производной поэтому Учитывая, что получим (по формуле 13). Последнее равенство означает, что дифференциал функции y = f(x), соответствующий данным значениям x и Δx, равен приращению ординаты касательной к кривой в данной точке x. В этом состоит геометрический смысл дифференциала.