 |
|
Определение производной, ее механический и геометрический смысл.
Сопоставляя операции, которые мы осуществляли при решении рассмотренных задач, легко усмотреть общие приемы. Обобщая их, придем к понятию производной.
Пусть функция  определена на промежутке Х. При каждом значении аргумента из этого промежутка функция
определена на промежутке Х. При каждом значении аргумента из этого промежутка функция  имеет некоторое значение.
имеет некоторое значение.
Пусть аргумент 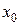 получил приращение Δx произвольное по знаку. Тогда функция
получил приращение Δx произвольное по знаку. Тогда функция  получит приращение Δy:
получит приращение Δy:  Составим отношение приращения функции к приращению аргумента:
Составим отношение приращения функции к приращению аргумента:  Найдем предел этого отношения при Δx → 0:
Найдем предел этого отношения при Δx → 0: 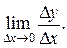
Если этот предел существует, то его называют производной («произведенной») данной функции  по независимой переменной x при данном её значении
по независимой переменной x при данном её значении  Обозначают производную одним из символов:
Обозначают производную одним из символов: 
О п р е д е л е н и е. Производной функции  в точке
в точке 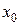 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

| (4) |
Таким образом, если существует производная при данном значении  то это определенное число. Если производная существует на всем промежутке, то она является функцией от x.
то это определенное число. Если производная существует на всем промежутке, то она является функцией от x.
Пользуясь введенным понятием производной, можно указать несколько примеров выявляющих понятие производной:
1) Скорость v прямолинейного движения материальной точки в момент времени t есть производная от пройденного пути S по времени t, т. е.  В этом заключается механический смысл производной.
В этом заключается механический смысл производной.
2) Производная  в точке x равна угловому коэффициентукасательной к графику функции
в точке x равна угловому коэффициентукасательной к графику функции  в точке, абсцисса которой равна x:
в точке, абсцисса которой равна x:
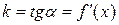
| (5) |
В этом заключается геометрический смысл производной.
3) Ускорение есть производная от скорости v по времени t, т. е. 
4) Теплоемкость тела есть производная от количества тепла по температуре, т. е. 
5) Сила тока есть производная от количества протекшего тока по времени, т. е. 
Обобщая можно сказать, что если функция описывает какой-либо физический процесс, то производная есть скорость протекания этого процесса. В этом заключается физический смысл производной.
Операция нахождения производной называется дифференцированием.
По определению можно вычислить производную любой элементарной функции.
П р и м е р 1.Найти производные функций по определению:
а) y = x²; б)  в)
в)  г)
г) 
Решение.
а) Придадим x приращение Δx. Тогда данная функция у получит приращение 
 Составим отношение приращения функции к приращению аргумента
Составим отношение приращения функции к приращению аргумента  Найдем предел этого отношения при Δx → 0 (по формуле 4), получим:
Найдем предел этого отношения при Δx → 0 (по формуле 4), получим: 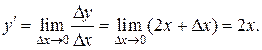
б) Придадим x приращение Δx, тогда данная функция у получит приращение 
 (использовали формулу для разности синусов двух углов). Составим отношение приращения функции к приращению аргумента и найдем его предел при
(использовали формулу для разности синусов двух углов). Составим отношение приращения функции к приращению аргумента и найдем его предел при  (формула 4):
(формула 4):  [учитывая, что
[учитывая, что  при
при  ]=
]= 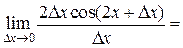
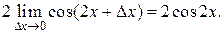
Следовательно, 
в) Аналогично, 
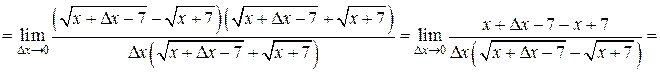

г) 

Проводя аналогичные рассуждения можно найти производные элементарных функций, которые приведены ниже.
Таблица основных формул дифференцирования
 , где , где 
| |||
 в частности в частности  , ,  , , 
| |||

| 
| ||
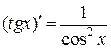
| 
| ||

| 
| ||

| 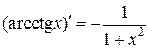
| ||

| 
|

| 
| ||

| 
| ||

| 
|