Главная | Обратная связь

Расчет на устойчивость

11.2.1 Расчет на устойчивость замкнутых круговых цилиндрических оболочек вращения, равномерно сжатых параллельно образующим, следует выполнять по формуле

(154)

где σ₁- расчетное напряжение в оболочке;

σ_cr,1 - критическое напряжение, равное меньшему из значений ψR_y или cEt / r (здесь r - радиус срединной поверхности оболочки; t - толщина оболочки) при r/t ≤ 300; при r/t > 300 σ_cr,1 = cEt / r.

Значения коэффициентов ψ при 0 < r/t ≤ 300 следует определять по формуле

(155)

Значения коэффициента с следует определять по таблице 34.

Таблица 34

r/t
с	0,22	0,18	0,16	0,14	0,11	0,09	0,08	0,07	0,06

В случае внецентренного сжатия параллельно образующим или чистого изгиба в диаметральной плоскости при касательных напряжениях в месте наибольшего момента, не превышающих значения 0,07E (t / r)^3/2,напряжение σ_cr,1 должно быть увеличено в (1,1 - 0,1 σ'₁/σ₁) раза, где σ'₁ - наименьшее напряжение (растягивающие напряжения считать отрицательными).

11.2.2 В трубах, рассчитываемых как сжатые или внецентренно-сжатые стержни при условной гибкости , должно быть выполнено условие

(156)

Такие трубы следует рассчитывать на устойчивость в соответствии с требованиями разделов 7 и 9 независимо от расчета на устойчивость стенок. Расчет на устойчивость стенок бесшовных или электросварных труб не требуется, если значения r/t не превышают половины значений, определяемых по формуле (156).

11.2.3 Цилиндрическая панель, опертая по двум образующим и двум дугам направляющей, равномерно сжатая вдоль образующих, при b²/(r t) ≤ 20 (где b - ширина панели, измеренная по дуге направляющей) должна быть рассчитана на устойчивость как пластинка по формулам:

при расчетном напряжении σ ≤ 0,8 R_y

(157)

при расчетном напряжении σ = R_y

(158)

При 0,8 R_y < σ < R_y наибольшее отношение b/t следует определять линейной интерполяцией.

Если b²/(r t) > 20, то панель следует рассчитывать на устойчивость как оболочку согласно требованиям 11.2.1.

11.2.4 Расчет на устойчивость замкнутой круговой цилиндрической оболочки вращения, при действии внешнего равномерного давления р, нормального к боковой поверхности, следует выполнять по формуле

(159)

где σ₂ = pr / t - расчетное кольцевое напряжение в оболочке;

σ_cr,2 - критическое напряжение, определяемое по формулам:

при 0,5 ≤ l / r ≤ 10

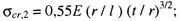(160)

при l / r ≥ 20

(161)

при 10 < l / r < 20 напряжение σ_cr,2 следует определять линейной интерполяцией.

Здесь l - длина цилиндрической оболочки.

Та же оболочка, но укрепленная кольцевыми ребрами, расположенными с шагом s ≥ 0,5r между осями, должна быть рассчитана на устойчивость по формулам (159) - (161) с подстановкой в них значения s вместо l.

В этом случае должно быть удовлетворено условие устойчивости ребра в своей плоскости как сжатого стержня согласно требованиям 7.1.3 при N = prs и расчетной длине стержня l_ef = 1,8r; при этом в сечение ребра следует включать участки оболочки шириной с каждой стороны от оси ребра, а условная гибкость стержня не должна превышать 6,5.

При одностороннем ребре жесткости его момент инерции следует вычислять относительно оси, совпадающей с ближайшей поверхностью оболочки.

(Опечатка. Июнь 2011 г.)

11.2.5 Расчет на устойчивость замкнутой круговой цилиндрической оболочки вращения, подверженной одновременному действию нагрузок, указанных в 11.2.1 и 11.2.4, следует выполнять по формуле

(162)

где σ_cr,1 должно быть вычислено согласно требованиям 11.2.1 и σ_cr,2 - согласно требованиям 11.2.4.

11.2.6 Расчет на устойчивость конической оболочки вращения с углом конусности β ≤ 60°, сжатой силой N вдоль оси (рисунок 18), следует выполнять по формуле

(163)

где N_cr - критическая сила, определяемая по формуле

(164)

здесь t - толщина оболочки;

σ_cr,1 - значение напряжения, вычисленное согласно требованиям 11.2.1 с заменой радиуса r радиусом r_т равным

(165)

Рисунок 18 - Схема конической оболочки вращения под действием продольного усилия сжатия

11.2.7 Расчет на устойчивость конической оболочки вращения при действии внешнего равномерного давления р, нормального к боковой поверхности, следует выполнять по формуле

(166)

здесь σ₂ = pr_m/t - расчетное кольцевое напряжение в оболочке;

σ_cr,2 - критическое напряжение, определяемое по формуле

(167)

где r_т - радиус, определяемый по формуле (165);

h - высота конической оболочки (между основаниями).

11.2.8 Расчет на устойчивость конической оболочки вращения, подверженной одновременному действию нагрузок, указанных в 11.2.6 и 11.2.7, следует выполнять по формуле

(168)

где значения N_cr и σ_cr,2следует вычислять по формулам (164) и (167).

11.2.9 Расчет на устойчивость полной сферической оболочки (или ее сегмента) при r / t ≤ 750 и действии внешнего равномерного давления р, нормального к ее поверхности, следует выполнять по формуле

(169)

где σ= pr /(2t) -расчетное напряжение;

σ_cr = 0,1 Et / r - критическое напряжение, принимаемое равным не более R_y;

здесь r - радиус срединной поверхности сферы.