Главная | Обратная связь

Прямая на плоскости.

НЕДЕЛЯ 3

Лекция 5.

 

Важнейшим понятием аналитической геометрии является уравнение линии.

Определение. Уравнение F(x, y)=0 называется уравнением линии L (в заданной системе координат), если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии L, и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

Любая прямая на плоскости задается уравнением первой степени относительно переменных х и у.

Прямую можно задать одним из следующих уравнений:

1. Уравнение прямой с угловым коэффициентом k (k – тангенс угла наклона прямой к положительному направлению оси Ox)

у=kх+b

2. Уравнение прямой с заданным угловым коэффициентом, проходящей через данную точку

3. Уравнение прямой, проходящей через две данные точки

4. Уравнение прямой в «отрезках»

здесь a и b –отрезки, которые отсекает прямая на осях О_х и О_у соответственно.

5. Нормальное уравнение прямой

 

 

здесь р – длина перпендикулярна, опущенного из начала координат на прямую, a -угол образованный этим перпендикуляром с положительным направлением оси Ох.

6. Уравнение прямой проходящей через точку , в данном направлении

 

7. Общее уравнение прямой

Ax=By+С=0.

 

Здесь A, B и C постоянные коэффициенты, причем 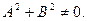Если какой-то коэффициент равен 0, то получаем неполные уравнения прямой.

А) Если А=0, тогда By+C=0 это уравнение определяет прямую, параллельную оси О_х.

б) Если В=0, то уравнение Ax+C=0 определяет прямую, параллельную оси О_у.

в) Если С=0, то уравнение Ax+By=0 задает прямую, проходящую через начало координат.

Г) Если А=С=0, то уравнение By=0 определяет прямую совпадающую с осью Ох.

Д) При В=С=0 прямая Ах=0 совпадает с осью Оу.

Прямые на плоскости могут пересекаться, быть параллельными или перпендикулярными.

Если прямые заданы уравнениями с угловым коэффициентом

y=k₁x+b₁ и y=k₂x+b₂

то острый угол между прямыми определяется по формулам

.

Если же прямые заданы общими уравнениями

А₁х+В₁у+С₁=0 и А₂х+В₂у+С₂=0

то угол между ними можно найти по формулам

Пусть прямые заданы уравнениями с угловым коэффициентом. Прямые параллельны, если tg a=0, тогда

k₂=k₁

условие параллельности двух прямых. Условие перпендикулярности определяет равенство

Если прямые заданы общими уравнениями, то условия параллельности и перпендикулярности примут вид:

,

А₁А₂+В₁В₂=0.

Литература: К,А, Хасеинов Каноны математики. Стр.61-77.

 

Лекция 6