 |
|
Практическое занятие 6
18. Написать уравнение окружности с центром в точке С(3;4) и радиусом 5.
Отв. A)  B)
B)  C)
C) 
D)  E)
E) 
19. Написать уравнение окружности, проходящей через начало координат с центром в точке С(-3;0).
Отв. A)  B)
B) 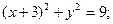 C)
C) 
D)  E)
E) 
20. Найти координаты центра и радиус окружности 
Отв. A) C(3;-4), R=6; B) C(3;4), R=6; C) C(-3;4), R=6;
D) C(-3;4), R=36; E) C(-6;8), R=16.
21. Составить уравнение окружности, для которой точки А(3;2) и В(-1;6) являются концами одного из диаметров.
Отв. . A)  B)
B)  C)
C) 
D)  E)
E) 
22. Окружность проходит через точку А(3;4), а ее центр находится в точке пересечения прямой  с ось. Ох.
с ось. Ох.
Отв. . A)  B)
B)  C)
C) 
D)  E)
E)  .
.
23. Найти координаты центра и радиус окружности 
Отв. A) C(1;-2), R=5; B) C(-1;2), R=5; C) C(-3;4), R=6;
D) C(-1;2), R=16; E) C(-2;1), R=6.
24. Определить уравнение линии центров двух окружностей:
а)  и
и 
б)  и
и 
Отв. А) 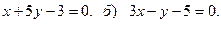
25. Составить уравнение окружности, если она проходит через точки А(3;1) и В(-1;3), а ее центр лежит на прямой 
Отв. 
26. Составить уравнение эллипса, фокусы которого расположены на оси абсцисс, симметрично относительно начала координат, если:
а) его полуоси равны 5 и 2;
б) его большая ось 2а =10, а расстояние между фокусами 2с = 8;
в) его малая ось равна 10, а расстояние между фокусами 2с = 8;
г) точка  принадлежит эллипсу и его малая полуось b = 3;
принадлежит эллипсу и его малая полуось b = 3;
д) точка  принадлежит эллипсу и его большая полуось а = 3;
принадлежит эллипсу и его большая полуось а = 3;
е) точка  принадлежит эллипсу и расстояние между его фокусами 2с = 8;
принадлежит эллипсу и расстояние между его фокусами 2с = 8;
ж) точки  и
и  принадлежать эллипсу.
принадлежать эллипсу.
Отв.
а) A)  ; B)
; B)  ; C)
; C)  ; D)
; D)  ;. E)
;. E) 
.
б) A)  ; B)
; B)  ; C)
; C)  ; D)
; D)  ; E)
; E)  .
.
в) A)  ; B)
; B)  ; C)
; C)  ;D)
;D)  ; E)
; E)  .
.
г) A)  ; B)
; B)  ; C)
; C)  ; D)
; D)  ; E)
; E)  .
.
д) A)  ; B)
; B)  ; C)
; C)  ; D)
; D)  ;. E)
;. E)  .
.
е) A)  ; B)
; B)  ; C)
; C)  ; D)
; D)  ; E)
; E)  .
.
ж) A)  ; B)
; B)  ; C)
; C)  ; D)
; D)  ; E)
; E)  .
.
27. Определить полуоси каждого из следующих эллипсов:
а) 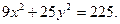 б)
б)  в)
в)  г)
г) 
Отв. а) A) a = 5, b = 3; B) a = 3, b = 5; C) a = 9, b = 5;
D) a = 1/5, b = 1/3; E) a = 3/5, b = 5/3.
б) a = 1/6, b = 1; B) a = 6, b = 1; C) a = 3, b = 6;
D) a = 9, b = 2; E) a = 1, b = 6;
в) A) a = 5/3, b = 3; B) a = 5, b = 3; C) a = 5/3, b = 1;
D) a = 9/25, b = 1; E) a = 5, b = 5;
г) A) a = 5, b = 1; B) a = 3/5, b = 4; C) a = 5, b = 3;
D) a = 5/3, b = 1/4; E) a = 3, b = 4.
28. Найти точки пересечения прямой  и эллипса
и эллипса 
Отв. A) (3;2), (4;3), B) (2;3), (4;3/2), C) (3;2), (4;3/2),
D) (3/2;2), (4/3;3/2), E) (2/3;2), (2;3/2).
29. Найти точки пересечения прямой  и эллипса
и эллипса 
Отв. A) (3;2), (4;3/2), B) (2;3), (4;3/2), C) (8/5;3),
D) (3;8/5), E) (2/3;2), (2;3/2).
30. Вычислить площадь четырехугольника, две вершины которого лежат в фокусах эллипса  а две другие совпадают с концами его малой оси.
а две другие совпадают с концами его малой оси.
Отв.  кв.ед.
кв.ед.
31. Найти полуоси, координаты фокусов и эксцентриситет эллипса, если известно, что эллипс проходит через точки  и
и 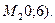
Отв. 
32. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс, симметрично относительно начала координат, если известно, что:
а) ее оси 2а = 10 и 2b = 8;
б) расстояние между фокусами 2с =10 и ось 2b =8;
в) расстояние между фокусами 2с =6 и эксцентриситет e = 3/2;
г) расстояние между фокусами 2с =10 и уравнения асимптот  ;
;
д) ось 2а = 16 и эксцентриситет e =5/4.
Отв. а) A)  ; B)
; B)  ; C)
; C)  ;
;
D)  ; E)
; E)  ;
;
б) A)  ; B)
; B)  ; C)
; C)  ;
;
D)  ; E)
; E)  ;
;
в) A) )  ; B)
; B)  ; C)
; C)  ;
;
D)  ; E)
; E)  ;
;
г) A)  ; B)
; B)  ; C)
; C)  ;
;
D)  ; E)
; E)  ;
;
д) A)  ; B)
; B)  ; C)
; C)  ;
;
D)  ; E)
; E)  .
.
33.Определить полуоси а и b каждой из следующих гипербол:
а)  б)
б)  в)
в)  г)
г)  д)
д) 
Отв. а) A) a = 4; b = 2; B) a = 2; b = 4; C) a = 2; b = 3;
D) a = 1/16; b = 1/2; E) a = 2; b = 3;
б) A) a = 6; b = 3; B) a = 2; b = 3; C) a = 1/2; b = 1/3;
D) a = 4; b = 9; E) a = 1/4; b = 1/3;
в) A) a = 2; b = 3; B) a = 1/2; b = 1/2; C) a = 2; b = 2;
D) a = 4; b = 2; E) a = 4; b = 4;
г) A) a = 3; b = 2; B) a = 1/9; b = 1/4; C) a = 1/2; b = 1/3;
D) a = 1/3; b = 1/2; E) a = 2; b = 3;
д) A) a = 1/4; b = 2; B) a = 1/16; b = 1/2; C) a = 2; b = 3;
D) a = 4; b = 2; E) a = 16; b = 2.
34. Гипербола проходит через точку  и имеет мнимую полуось
и имеет мнимую полуось
b = 2. Написать ее уравнение и найти фокальные радиусы точки М
Отв. 
35. На гиперболе  взята точка М с ординатой, равной 1. Найти расстояние ее от фокусов.
взята точка М с ординатой, равной 1. Найти расстояние ее от фокусов.
Отв. 
36. Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы - в вершинах эллипса 
Отв. 
37. Дана гипербола  Найти:
Найти:
а) полуоси а и b; б) фокусы; в) эксцентриситет; г) уравнения асимптот.
Отв. а) а = 3, b = 4; б)  в)
в)  г)
г) 
38. Найти точки пересечения прямой  и гиперболы
и гиперболы 
Отв. (6;2) и 
39 . Найти точки пересечения прямой 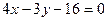 и гиперболы
и гиперболы 
Отв. (6;2) и  - прямая касается гиперболы.
- прямая касается гиперболы.
40. Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С. полуоси, эксцентриситет и уравнения асимптот:
1) 
2) 
3) 
Отв.
1) С(2;-3), а = 3,b = 4, e=53, уравнения асимптот:  2) С(-5;1), а = 8, b = 6, e=54,уравнения асимптот:
2) С(-5;1), а = 8, b = 6, e=54,уравнения асимптот: 
3) С(2;-1), а = 3, b = 4, e=54, уравнения асимптот: 
41. Составить уравнение параболы, вершина которой находится в начале координат, зная, что:
а) парабола расположена симметрично относительно оси Ох и проходит через точку А(9;6);
б) парабола расположена симметрично относительно оси Ох и проходит через точку В(-1;3);
в) парабола расположена симметрично относительно оси Оу и проходит через точку С(1;1)
г) парабола расположена симметрично относительно оси Оу и проходит
через точку D(4;-8).
Отв. а) A)  ; B)
; B)  ; C)
; C)  ; D)
; D)  ; E)
; E)  .
.
б) A)  ; B)
; B)  ; C)
; C)  ; D)
; D)  ; E)
; E)  .
.
в) A)  ; B)
; B)  ; C)
; C)  ; D)
; D)  ; E)
; E)  .
.
г) A)  ; B)
; B)  ; C)
; C)  ; D)
; D)  ; E)
; E)  .
.
42. Написать уравнение окружности, имеющей центр в фокусе параболы  и касающейся ее директрисы. Найти точки пересечения параболы и окружности. Отв.
и касающейся ее директрисы. Найти точки пересечения параболы и окружности. Отв. 
43. Написать уравнение параболы и уравнение директрисы, если известно, что парабола симметрична относительно оси Ох и что точка пересечения прямых у = х и х + у = 2 лежит на параболе.
Отв.  .
.
44. Найти фокус F и уравнение директрисы параболы 
Отв. A) F(12;0), x + 12 = 0; B) F(3;0), x + 3 = 0; C) F(4;0), x + 4 = 0;
D) F(6;0), x + 6 = 0; E) F(-6;0), x - 6 = 0.
45. Вычислить фокальный радиус точки М параболы  если абсцисса точки М равна 7.
если абсцисса точки М равна 7.
Отв. A) 24. B) 17. C) 27. D) 20. E) 12.
46. Вычислить фокальный радиус точки М параболы  если ордината точки М равна 6.
если ордината точки М равна 6.
Отв. A) 6. B) 12. C) 4. D) 10. E) 12.
47. Установить, что каждое из следующих уравнений определяет параболу, и найти координаты ее вершины А и величину параметра р.
а) 
Отв. а) A) A(-2;1), p = 2, B) A(2;1), p = -2, C) A(2;3), p = 2,
D) A(-1;2), p = 1, E) A(2;1), p = 2.
б) A) A(3;1), p = 1/2, B) A(1;3),p = 1/8, C) A(1;2),p = 2/3,
D) A(1;3), p = 1/4, E) A(-1;1), p = ½.
в) A) A(6;1), p = 3, B) A(-2;-1), p = 3, C) A(6;-1),p = 3,
D) A(12;-1), p = 2, E) A(-2;1),p = 3.
Литература:Линейная и векторная алгебра. Аналитическая геометрия. Сборник задач по высшей математике. Академия ГА Алматы 2010. Стр 36-45.