 |
|
Протокол Нидхема-Шрёдера для аутентификации с симметричным ключом

Протокол Нидхема-Шрёдера для аутентификации с симметричным ключом
При схеме шифрования с симметричным ключом, предполагается, что секретный ключ известен исерверу аутентификации  (Трент) и обоим субъектам обмена:
(Трент) и обоим субъектам обмена: 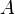 (Алиса) и
(Алиса) и 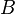 (Боб). Изначально оба субъекта имеют секретные ключи:
(Боб). Изначально оба субъекта имеют секретные ключи: 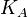 и
и 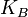 , известные только им и некоторой доверенной стороне - серверу аутентификации. В ходе выполнения протокола Алиса и Боб получают от сервера новый секретный сессионный ключ для шифрования взаимных сообщений в данном сеансе связи, т.е. сообщения от Алисы к Бобу дешифровать может только Боб, сообщения от Боба к Алисе дешифровать может только Алиса. Кроме того субъекты обмена должны быть уверены, что пришедшее сообщение было отправлено именно тем, с кем должен произойти обмен. Боб должен быть уверен, что получил сообщение именно от Алисы и наоборот. Это также обеспечивается протоколом. Предположим, что обмен инициирует Алиса. Будем полагать, что сервер аутентификации у них общий. Рассмотрим реализацию протокола[4]:
, известные только им и некоторой доверенной стороне - серверу аутентификации. В ходе выполнения протокола Алиса и Боб получают от сервера новый секретный сессионный ключ для шифрования взаимных сообщений в данном сеансе связи, т.е. сообщения от Алисы к Бобу дешифровать может только Боб, сообщения от Боба к Алисе дешифровать может только Алиса. Кроме того субъекты обмена должны быть уверены, что пришедшее сообщение было отправлено именно тем, с кем должен произойти обмен. Боб должен быть уверен, что получил сообщение именно от Алисы и наоборот. Это также обеспечивается протоколом. Предположим, что обмен инициирует Алиса. Будем полагать, что сервер аутентификации у них общий. Рассмотрим реализацию протокола[4]:
1. 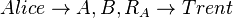
2. 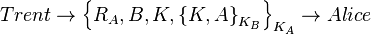
3. 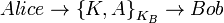
4. 
5. 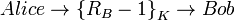
Обмен начинается с того, что Алиса генерирует некоторое случайное число 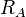 (идентификатор), использующееся один раз. Первое сообщение от Алисы к Тренту содержит в себе имена участников предстоящего обмена и генерированное Алисой случайное число:
(идентификатор), использующееся один раз. Первое сообщение от Алисы к Тренту содержит в себе имена участников предстоящего обмена и генерированное Алисой случайное число:
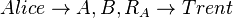
Данное сообщение посылается открытым текстом, но может быть зашифровано ключом Алисы 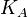 :
:
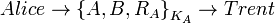
При получении этого сообщения Трент извлекает из базы данных секретные ключи Алисы и Боба: 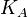 и
и 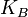 , а также вычисляет новый сессионный ключ
, а также вычисляет новый сессионный ключ 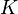 . Далее Трент посылает Алисе следующее сообщение:
. Далее Трент посылает Алисе следующее сообщение:
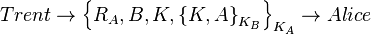
Алиса может дешифровать и прочесть сообщение от Трента. Она проверяет наличие своего идентификатора 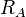 в сообщении, что подтверждает то, что данное сообщение является откликом на ее первое сообщение Тренту. Также она проверяет имя субъекта, с которым собирается обмениваться данными. Эта проверка обязательна, так как если бы не было этого имени, Злоумышленник мог бы заменить имя Боба на свое в первом сообщении, и Алиса, ничего не подозревая, в дальнейшем бы взаимодействовала со Злоумышленником. Часть сообщения Алиса прочитать не может, так как эта часть зашифрована ключом Боба. Алиса пересылает Бобу зашифрованный его ключём фрагмент:
в сообщении, что подтверждает то, что данное сообщение является откликом на ее первое сообщение Тренту. Также она проверяет имя субъекта, с которым собирается обмениваться данными. Эта проверка обязательна, так как если бы не было этого имени, Злоумышленник мог бы заменить имя Боба на свое в первом сообщении, и Алиса, ничего не подозревая, в дальнейшем бы взаимодействовала со Злоумышленником. Часть сообщения Алиса прочитать не может, так как эта часть зашифрована ключом Боба. Алиса пересылает Бобу зашифрованный его ключём фрагмент:
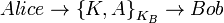
Дешифровать его может только Боб, так как оно зашифровано его секретным ключом. После дешифровки Боб тоже владеет сессионным ключом 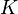 . Имя Алисы в сообщении подтверждает факт, что сообщение от неё. Далее при обмене данными будет использоваться сессионный ключ. Чтобы сделать схему симметричной и уменьшить вероятность атаки воспроизведения, Боб генерирует некоторое случайное число
. Имя Алисы в сообщении подтверждает факт, что сообщение от неё. Далее при обмене данными будет использоваться сессионный ключ. Чтобы сделать схему симметричной и уменьшить вероятность атаки воспроизведения, Боб генерирует некоторое случайное число 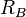 (идентификатор Боба) и посылает Алисе следующее сообщение, зашифрованное сессионным ключом:
(идентификатор Боба) и посылает Алисе следующее сообщение, зашифрованное сессионным ключом:

Алиса дешифрует его и посылает отклик, который ожидает Боб, также зашифрованный сессионным ключом:
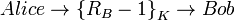
Для регулярно взаимодействующих партнёров можно сократить число сообщений до трёх, убрав первые два. При этом ключ будет использоваться многократно[5
Один из важных моментов, который следует принимать во внимание при генерировании и хранении ключей, — это продолжительность их жизни. Общее правило состоит в том, что чем дольше используемый ключ находится в обращении, тем легче нападающему его вскрыть, и тем большую ценность он для него представляет. Кроме того, важно правильно уничтожить ключ по истечении его жизни. Перекладывание проблемы на плечи операционной системы командой del или rem не гарантирует того, что нападающий не сможет восстановить информацию, исследуя жесткий диск. Обычно удаление файла не стирает его содержания, а всего лишь сообщает системе о том, что ячейки памяти, отведенные под него, теперь свободны для записи новых данных.
№ 14 Ключевая информация: сеансовый, секретный, мастер-ключ, открытый и закрытый ключ. Требования к качеству ключевой информации и источнику ключей.
Ключ — секретная информация, используемая криптографическим алгоритмом при шифровании/расшифровке сообщений, постановке и проверке цифровой подписи, вычислении кодов аутентичности (MAC). При использовании одного и того же алгоритма результат шифрования зависит от ключа. Для современных алгоритмов сильной криптографии утрата ключа приводит к практической невозможности расшифровать информацию.
Согласно принципу Керхгоффса, надёжность криптографической системы должна определяться сокрытием секретных ключей, но не сокрытием используемых алгоритмов или их особенностей.
[править]Длина ключа
Количество информации в ключе, как правило, измеряется в битах.
Для современных симметричных алгоритмов (AES, CAST5, IDEA, Blowfish, Twofish) основной характеристикой криптостойкости является длина ключа. Шифрование с ключами длиной 128 бит и выше считается сильным, так как для расшифровки информации без ключа требуются годы работы мощных суперкомпьютеров. Для асимметричных алгоритмов, основанных на проблемах теории чисел (проблема факторизации — RSA, проблема дискретного логарифма — Elgamal) в силу их особенностей минимальная надёжная длина ключа в настоящее время — 1024 бит. Для асимметричных алгоритмов, основанных на использовании теории эллиптических кривых (ECDSA, ГОСТ Р 34.10-2001, ДСТУ 4145-2002), минимальной надёжной длиной ключа считается 163 бит, но рекомендуются длины от 191 бит и выше.
[править]Классификация ключей
Криптографические ключи различаются согласно алгоритмам, в которых они используются.
· Секретные (Симметричные) ключи — ключи, используемые в симметричных алгоритмах (шифрование, выработка кодов аутентичности). Главное свойство симметричных ключей: для выполнения как прямого, так и обратного криптографического преобразования (шифрование/расшифровывание, вычисление MAC/проверка MAC) необходимо использовать один и тот же ключ (либо же ключ для обратного преобразования легко вычисляется из ключа для прямого преобразования, и наоборот). С одной стороны, это обеспечивает более высокую конфиденциальность сообщений, с другой стороны, создаёт проблемы распространения ключей в системах с большим количеством пользователей.
· Асимметричные ключи — ключи, используемые в асимметричных алгоритмах (шифрование, ЭЦП); вообще говоря, являются ключевой парой, поскольку состоят из двух ключей:
· Закрытый ключ (en:Private key) — ключ, известный только своему владельцу. Только сохранение пользователем в тайне своего закрытого ключа гарантирует невозможность подделки злоумышленником документа и цифровой подписи от имени заверяющего.
· Открытый ключ (en:Public key) — ключ, который может быть опубликован и используется для проверки подлинности подписанного документа, а также для предупреждения мошенничества со стороны заверяющего лица в виде отказа его от подписи документа. Открытый ключ подписи вычисляется, как значение некоторой функции от закрытого ключа, но знание открытого ключа не дает возможности определить закрытый ключ.
Главное свойство ключевой пары: по секретному ключу легко вычисляется открытый ключ, но по известному открытому ключу практически невозможно вычислить секретный. В алгоритмах ЭЦП подпись обычно ставится на секретном ключе пользователя, а проверяется на открытом. Таким образом, любой может проверить, действительно ли данный пользователь поставил данную подпись. Тем самым асимметричные алгоритмы обеспечивают не только целостность информации, но и её аутентичность. При шифровании же наоборот, сообщения шифруются на открытом ключе, а расшифровываются на секретном. Таким образом, расшифровать сообщение может только адресат и больше никто (включая отправителя). Использование асимметричных алгоритмов снимает проблему распространения ключей пользователей в системе, но ставит новые проблемы: достоверность полученных ключей. Эти проблемы более-менее успешно решаются в рамках инфраструктуры открытых ключей (PKI).
· Сеансовые (сессионные) ключи — ключи, вырабатываемые между двумя пользователями, обычно для защиты канала связи. Обычно сеансовым ключом являетсяобщий секрет — информация, которая вырабатывается на основе секретного ключа одной стороны и открытого ключа другой стороны. Существует несколько протоколов выработки сеансовых ключей и общих секретов, среди них, в частности, алгоритм Диффи — Хеллмана.
· Подключи — ключевая информация, вырабатываемая в процессе работы криптографического алгоритма на основе ключа. Зачастую подключи вырабатываются на основе специальной процедуры развёртывания ключа.
При накоплении ключи нельзя записывать в явном виде на носители. Для повышения безопасности ключ должен быть зашифрован другим ключом, другой - третьим и т. д. Последний ключ в этой иерархии шифровать не нужно, но его следует размещать в защищенной части аппаратуры. Такой ключ называется мастер-ключом.
Для двух участников А и B распределение ключа может быть выполнено одним из следующих способов.
1. Ключ может быть создан А и физически передан B.
2. Третья сторона может создать ключ и физически передать его А и B.
3. А и В имеют предварительно созданный и недолго используемый ключ, один участник может передать новый ключ другому, применив для шифрования старый ключ.
4. Если А и В каждый имеют безопасное соединение с третьим участником C, C может передать ключ по этому безопасному каналу А и B.
Первый и второй способы называются ручным распределением ключа. Это самые надежные способыраспределения ключа, однако во многих случаях пользоваться ими неудобно и даже невозможно. В распределенной системе любой хост или сервер должен иметь возможность обмениваться конфиденциальной информацией со многими аутентифицированными хостами и серверами. Таким образом, каждый хост должен иметь набор ключей, поддерживаемый динамически. Проблема особенно актуальна в больших распределенных системах.
Количество требуемых ключей зависит от числа участников, которые должны взаимодействовать. Если выполняется шифрование на сетевом или IP-уровне, то ключ необходим для каждой пары хостов в сети. Таким образом, если есть N хостов, то необходимое число ключей [N (N - 1)]/2. Если шифрование выполняется на прикладном уровне, то ключ нужен для каждой пары прикладных процессов, которых гораздо больше, чем хостов.
Третий способ распределения ключей может применяться на любом уровне стека протоколов, но если атакующий получает возможность доступа к одному ключу, то вся последовательность ключей будет раскрыта. Более того, все равно должно быть проведено первоначальное распространение большого количества ключей.
Поэтому в больших автоматизированных системах широко применяются различные варианты четвертого способа. В этой схеме предполагается существование так называемого центра распределения ключей (Key Destribution Centre - KDC ), который отвечает за распределение ключей для хостов, процессов и приложений. Каждый участник должен разделять уникальный ключ с KDC.
Использование центра распределения ключей основано на использовании иерархии ключей. Как минимум используется два типа ключей: мастер-ключии ключи сессии.
Для обеспечения конфиденциальной связи между конечными системами используется временный ключ, называемый ключом сессии . Обычно ключ сессии используется для шифрования транспортного соединения и затем уничтожается. Каждый ключ сессии должен быть получен по сети из центра распределения ключей. Ключи сессии передаются в зашифрованном виде, используя мастер-ключ, который разделяется между центром распределения ключей и конечной системой.
№15 Распределение секретных ключей. Обмен ключами по Диффи-Хельмана.
Распределение ключей
Физическое распределение. С помощью доверенных курьеров или вооруженной охраны ключи могут рассылаться традиционным физическим путем. До семидесятых годов двадцатого века это действительно был единственный безопасный путь распределения ключей при установке системы. Ему сопутствовал ряд трудностей, в особенности при расширении, масштабировании (модульном наращивании системы в рамках унифицированной архитектуры) криптосистемы, но основной недостаток, связанный с таким способом распределения, состоит в том, что криптостойкость системы зависит не столько от ключа, сколько от курьера. Если подкупить, похитить или просто убить курьера, то система будет скомпрометирована.
^ Распределение с помощью протоколов с секретным ключом. Если долговременные секретные ключи распределены между пользователями и неким центром, который обычно называют центром доверия, то его можно использовать для генерирования ключей и обмена между любыми двумя пользователями всякий раз, когда в этом возникает необходимость. Протоколы, предназначенные для этой цели, — предмет обсуждения настоящей главы. Обычно они достаточно эффективны, но не лишены и недостатков. В частности, этот способ распределения предусматривает, что как оба пользователя, так и центр работают в режиме онлайн. Кроме того, статичные ключи при этом должны распределяться физическим путем.
^ Распределение с помощью протоколов с открытым ключом. Используя криптосистемы с открытым ключом, партнеры, не доверяющие посредникам и лишенные возможности встретиться, могут договориться об общем секретном ключе в режиме онлайн в соответствии с протоколом об обмене ключей. Это наиболее распространенное приложение техники шифрования с открытым ключом. Вместо того, чтобы шифровать большой объем данных непосредственно с помощью открытого ключа, стороны предварительно согласовывают секретный ключ. Затем для шифрования фактической информации применяется симметричный шифр с согласованным ключом.
Алгори́тм Ди́ффи — Хе́ллмана (англ. Diffie-Hellman, DH) позволяет двум или более пользователям обменяться без посредников ключом, который может быть использован затем для симметричного шифрования. [1]
Данный алгоритм не применяется для шифрования сообщений или формирования электронной подписи. Его назначение – в распределении ключей.
Это была первая криптосистема, которая позволяла защищать информацию без использования секретных ключей, передаваемых по защищенным каналам.
Схема открытого распределения ключей, предложенная Диффи и Хеллманом, произвела настоящую революцию в мире шифрования, так как снимала основную проблему классической криптографии – проблему распределения ключей.
Описание алгоритма
Предположим, существует два абонента: Алиса и Боб. Обоим абонентам известны некоторые два числа g и p, которые не являются секретными и могут быть известны также другим заинтересованным лицам. Для того, чтобы создать неизвестный более никому секретный ключ, оба абонента генерируют большие случайные числа: Алиса — число a, Боб— число b. Затем Алиса вычисляет значение[5] (1):
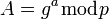 (1)
(1)
и пересылает его Бобу , а Боб вычисляет (2):
 (2)
(2)
и передаёт Алисе. Предполагается, что злоумышленник может получить оба этих значения, но не модифицировать их (то есть у него нет возможности вмешаться в процесс передачи).
На втором этапе Алиса на основе имеющегося у нее a и полученного по сети B вычисляет значение (3):
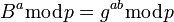 (3)
(3)
Боб на основе имеющегося у него b и полученного по сети A вычисляет значение (4):
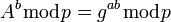 (4)
(4)
Как нетрудно видеть, у Алисы и Боба получилось одно и то же число (5):
 (5)
(5)
Его они и могут использовать в качестве секретного ключа, поскольку здесь злоумышленник встретится с практически неразрешимой (за разумное время) проблемой вычисления (3) или (4) по перехваченным 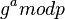 и
и 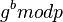 , если числа p,a,b выбраны достаточно большими. Наглядная работа алгоритма показана на рисунке[6].
, если числа p,a,b выбраны достаточно большими. Наглядная работа алгоритма показана на рисунке[6].


Алгоритм Диффи — Хеллмана, где K — итоговый общий секретный ключ
При работе алгоритма, каждая сторона:
1. генерирует случайное натуральное число a — закрытый ключ
2. совместно с удалённой стороной устанавливает открытые параметры p и g (обычно значения p и g генерируются на одной стороне и передаются другой), где
p является случайным простым числом
g является первообразным корнем по модулю p
3. вычисляет открытый ключ A, используя преобразование над закрытым ключом
A = ga mod p
4. обменивается открытыми ключами с удалённой стороной
5. вычисляет общий секретный ключ K, используя открытый ключ удаленной стороны B и свой закрытый ключ a
K = Ba mod p
К получается равным с обеих сторон, потому что:
Ba mod p = (gb mod p)a mod p = gab mod p = (ga mod p)b mod p = Ab mod p
В практических реализациях, для a и b используются числа порядка 10100 и p порядка 10300. Число g не обязано быть большим и обычно имеет значение в пределах первого десятка.
№ 16 Криптосистемы RSA и Эль-Гамаля.
RSA (аббревиатура от фамилий Rivest, Shamir и Adleman) — криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел.
Введение
Криптографические системы с открытым ключом используют так называемые односторонние функции, которые обладают следующим свойством:
· Если известно  , то
, то  вычислить относительно просто
вычислить относительно просто
· Если известно  , то для вычисления
, то для вычисления  нет простого (эффективного) пути.
нет простого (эффективного) пути.
Под односторонностью понимается не теоретическая однонаправленность, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства, за обозримый интервал времени.
В основу криптографической системы с открытым ключом RSA положена сложность задачи факторизации произведения двух больших простых чисел. Для шифрования используется операция возведения в степень по модулю большого числа. Для дешифрования за разумное время (обратной операции) необходимо уметь вычислять функцию Эйлера от данного большого числа, для чего необходимо знать разложения числа на простые множители.
В криптографической системе с открытым ключом каждый участник располагает как открытым ключом (англ. public key), так и закрытым ключом (англ. secret key). В криптографической системе RSA каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и закрытый ключ самостоятельно. Закрытый ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их. Открытый и закрытый ключи каждого участника обмена сообщениями в криптосистеме RSA образуют «согласованную пару» в том смысле, что они являются взаимно обратными, то есть:
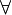 сообщения
сообщения 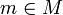 , где
, где  — множество допустимых сообщений
— множество допустимых сообщений
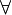 допустимых открытого и закрытого ключей
допустимых открытого и закрытого ключей 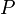 и
и 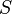
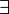 соответствующие функции шифрования
соответствующие функции шифрования 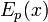 и расшифрования
и расшифрования 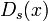 , такие что
, такие что

[править]Алгоритм создания открытого и секретного ключей
RSA-ключи генерируются следующим образом:[14]
1. Выбираются два различных случайных простых числа 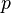 и
и 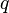 заданного размера (например, 1024 бита каждое).
заданного размера (например, 1024 бита каждое).
2. Вычисляется их произведение 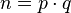 , которое называется модулем.
, которое называется модулем.
3. Вычисляется значение функции Эйлера от числа 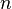 :
:
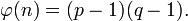
4. Выбирается целое число  (
( 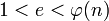 ), взаимно простое со значением функции
), взаимно простое со значением функции  . Обычно в качестве
. Обычно в качестве  берут простые числа, содержащие небольшое количество единичных бит в двоичной записи, например, простые числа Ферма 17, 257 или 65537.
берут простые числа, содержащие небольшое количество единичных бит в двоичной записи, например, простые числа Ферма 17, 257 или 65537.
· Число  называется открытой экспонентой (англ. public exponent)
называется открытой экспонентой (англ. public exponent)
· Время, необходимое для шифрования с использованием быстрого возведения в степень, пропорционально числу единичных бит в  .
.
· Слишком малые значения  , например 3, потенциально могут ослабить безопасность схемы RSA.[15]
, например 3, потенциально могут ослабить безопасность схемы RSA.[15]
5. Вычисляется число  , мультипликативно обратное к числу
, мультипликативно обратное к числу  по модулю
по модулю  , то есть число, удовлетворяющее условию:
, то есть число, удовлетворяющее условию:
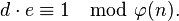
· Число  называется секретной экспонентой. Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.
называется секретной экспонентой. Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.
6. Пара 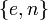 публикуется в качестве открытого ключа RSA (англ. RSA public key).
публикуется в качестве открытого ключа RSA (англ. RSA public key).
7. Пара 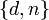 играет роль закрытого ключа RSA (англ. RSA private key) и держится в секрете.
играет роль закрытого ключа RSA (англ. RSA private key) и держится в секрете.
[править]Шифрование и расшифрование
Предположим, Боб хочет послать Алисе сообщение 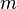 .
.
Сообщениями являются целые числа в интервале от 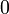 до
до 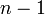 , т.е
, т.е 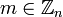 .
.

Алгоритм:[14]
· Взять открытый ключ 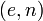 Алисы
· Взять открытый текст Алисы
· Взять открытый текст 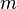 · Зашифровать сообщение с использованием открытого ключа Алисы:
· Зашифровать сообщение с использованием открытого ключа Алисы:

| Алгоритм:
· Принять зашифрованное сообщение  · Взять свой закрытый ключ
· Взять свой закрытый ключ 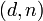 · Применить закрытый ключ для расшифрования сообщения:
· Применить закрытый ключ для расшифрования сообщения:
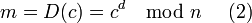
|
Наиболее используемым в настоящее время является смешанный алгоритм шифрования, в котором сначала шифруется сеансовый ключ, а потом уже с его помощью участники шифруют свои сообщения симметричными системами. После завершения сеанса сеансовый ключ как правило уничтожается.
Алгоритм шифрования сеансового ключа выглядит следующим образом[16]:
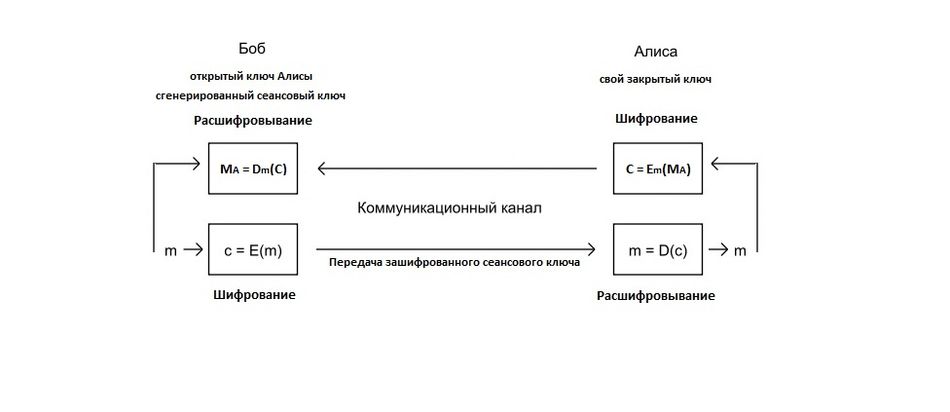
Алгоритм:
· Взять открытый ключ 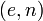 Алисы
· Создать случайный сеансовый ключ Алисы
· Создать случайный сеансовый ключ 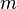 · Зашифровать сеансовый ключ с использованием открытого ключа Алисы:
· Зашифровать сеансовый ключ с использованием открытого ключа Алисы:
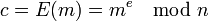 · Расшифровать сообщение
· Расшифровать сообщение  с помощью сеансового ключа симметричным алгоритмом: с помощью сеансового ключа симметричным алгоритмом:
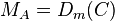
| Алгоритм:
· Принять зашифрованный сеансовый ключ Боба  · Взять свой закрытый ключ
· Взять свой закрытый ключ 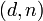 · Применить закрытый ключ для расшифровывания сеансового ключа:
· Применить закрытый ключ для расшифровывания сеансового ключа:
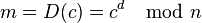 · Зашифровать сообщение
· Зашифровать сообщение 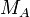 с помощью сеансового ключа симметричным алгоритмом: с помощью сеансового ключа симметричным алгоритмом:

|
В случае, когда сеансовый ключ больше, чем модуль 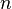 сеансовый ключ разбивают на блоки нужной длины (в случае необходимости дополняют нулями) и шифруют каждый блок.
сеансовый ключ разбивают на блоки нужной длины (в случае необходимости дополняют нулями) и шифруют каждый блок.
Схема Эль-Гамаля (Elgamal) — криптосистема с открытым ключом,основанная на трудности вычисления дискретных логарифмов в конечном поле. Криптосистема включает в себя алгоритм шифрования и алгоритм цифровой подписи. Схема Эль-Гамаля лежит в основе стандартов электронной цифровой подписи в США (DSA) иРоссии (ГОСТ Р 34.10-94).
Генерация ключей
1. Генерируется случайное простое число 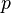 длины
длины 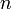 битов.
битов.
2. Выбирается случайный примитивный элемент  поля
поля 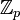 .
.
3. Выбирается случайное целое число 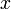 такое, что
такое, что 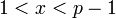 .
.
4. Вычисляется  .
.
5. Открытым ключом является тройка 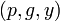 , закрытым ключом — число
, закрытым ключом — число 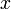 .
.
[править]Работа в режиме шифрования
Шифросистема Эль-Гамаля является фактически одним из способов выработки открытых ключей Диффи — Хеллмана. Шифрование по схеме Эль-Гамаля не следует путать с алгоритмом цифровой подписи по схеме Эль-Гамаля.
[править]Шифрование
Сообщение 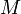 шифруется следующим образом:
шифруется следующим образом:
1. Выбирается сессионный ключ — случайное целое число 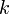 такое, что
такое, что 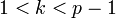
2. Вычисляются числа 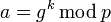 и
и 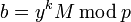 .
.
3. Пара чисел  является шифротекстом.
является шифротекстом.
Нетрудно видеть, что длина шифротекста в схеме Эль-Гамаля длиннее исходного сообщения  вдвое.
вдвое.
[править]Расшифрование
Зная закрытый ключ 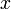 , исходное сообщение можно вычислить из шифротекста
, исходное сообщение можно вычислить из шифротекста  по формуле:
по формуле:
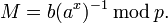
При этом нетрудно проверить, что
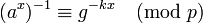
и поэтому
 .
.
Для практических вычислений больше подходит следующая формула:
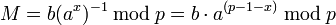
[править]Схема шифрования
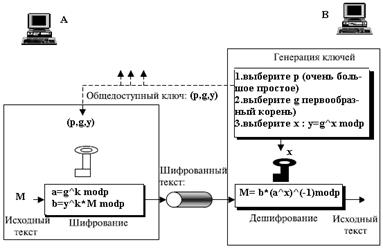
№ 17 Криптографические функции аутентификации.
Имитовста́вка (MAC, англ. message authentication code — код аутентичности сообщения) — средство обеспечения имитозащиты в протоколах аутентификациисообщений с доверяющими друг другу участниками — специальный набор символов, который добавляется к сообщению и предназначен для обеспечения его целостности и аутентификации источника данных.
MAC обычно применяется для обеспечения целостности и защиты от фальсификации передаваемой информации.
Для проверки целостности (но не аутентичности) сообщения на отправляющей стороне к сообщению добавляется значение хеш-функции от этого сообщения, на приемной стороне также вырабатывается хеш от полученного сообщения. Выработанный на приёмной стороне и полученный хеш сравниваются, если они равны то считается, что полученное сообщение дошло без изменений.
Для защиты от фальсификации (имитации) сообщения применяется имитовставка, выработанная с использованием секретного элемента (ключа), известного только отправителю и получателю.
Простым способом преобразовать однонаправленную хэш-функцию в имитовставку (MAC) является шифрование хэш-значения симметричным алгоритмом. Такой MAC может быть преобразован в однонаправленную хэш-функцию с помощью раскрытия ключа.
Другим способом является выработка имитовставки (MAC) с помощью специализированного алгоритма имитозащиты на основе симметричного алгоритма шифрования.
CBC-MAC: Простейшим способом создать зависящую от ключа имитовставку — шифрование сообщения блочным алгоритмом в режимах CBC или CFB. Имитовставкой является последний шифрованный блок, зашифрованный в этих режимах. Потенциальная проблема, связанная с безопасностью этого метода, состоит в том, что получатель должен знать ключ, и этот ключ позволяет ему генерировать сообщения с тем же значением имитовставки, что и у присланного сообщения, таким образом, имитовставка на основе симметричного шифра не дает знания — отправитель или получатель сформировал эту имитовставку. Отсюда следует, что имитовставка на основе симметричного шифра не может заменять собой электронную подпись.
Хеширование (иногда «хэширование», англ. hashing) — преобразование по детерминированному алгоритму входного массива данных произвольной длины в выходнуюбитовую строку фиксированной длины. Такие преобразования также называются хеш-функциями или функциями свёртки, а их результаты называют хешем, хеш-кодом или сводкой сообщения (англ. message digest). Если у двух строк хеш-коды разные, строки гарантированно различаются, если одинаковые — строки, вероятно, совпадают.
Среди множества существующих хеш-функций принято выделять криптографически стойкие, применяемые в криптографии, так как на них накладываются дополнительные требования. Для того чтобы хеш-функция 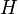 считалась криптографически стойкой, она должна удовлетворять трем основным требованиям, на которых основано большинство применений хеш-функций в криптографии:
считалась криптографически стойкой, она должна удовлетворять трем основным требованиям, на которых основано большинство применений хеш-функций в криптографии:
· Необратимость: для заданного значения хеш-функции m должно быть вычислительно неосуществимо найти блок данных 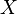 , для которого
, для которого 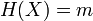 .
.
· Стойкость к коллизиям первого рода: для заданного сообщения M должно быть вычислительно неосуществимо подобрать другое сообщение N, для которого 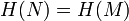 .
.
· Стойкость к коллизиям второго рода: должно быть вычислительно неосуществимо подобрать пару сообщений 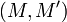 , имеющих одинаковый хеш.
, имеющих одинаковый хеш.
Данные требования не являются независимыми:
· Обратимая функция нестойка к коллизиям первого и второго рода.
· Функция, нестойкая к коллизиям первого рода, нестойка к коллизиям второго рода; обратное неверно.
Следует отметить, что не доказано существование необратимых хеш-функций, для которых вычисление какого-либо прообраза заданного значения хеш-функции теоретически невозможно. Обычно нахождение обратного значения является лишь вычислительно сложной задачей.
Атака «дней рождения» позволяет находить коллизии для хеш-функции с длиной значений n битов в среднем за примерно  вычислений хеш-функции. Поэтому n-битная хеш-функция считается криптостойкой, если вычислительная сложность нахождения коллизий для неё близка к
вычислений хеш-функции. Поэтому n-битная хеш-функция считается криптостойкой, если вычислительная сложность нахождения коллизий для неё близка к  .
.
Для криптографических хеш-функций также важно, чтобы при малейшем изменении аргумента значение функции сильно изменялось (лавинный эффект). В частности, значение хеша не должно давать утечки информации даже об отдельных битах аргумента. Это требование является залогом криптостойкости алгоритмов хеширования, хеширующих пользовательский пароль для получения ключа.[7]
Хеширование часто используется в алгоритмах электронно-цифровой подписи, где шифруется не само сообщение, а его хеш-код, что уменьшает время вычисления, а также повышает криптостойкость. Также в большинстве случаев, вместо паролей хранятся значения их хеш-кодов.