Главная | Обратная связь

Назначение и принцип построения компараторов четырехразрядных двоичных чисел

Компаратором (устройством сравнения) называется КЦУ, которое предназначено для сравнения двух двоичных чисел. УГО компаратора четырехразрядных двоичных чисел (рисунок 4.3) представляет собой прямоугольник с аббревиатурой COMP во внутреннем поле (от англ. Comparator) [6].

 

Рисунок 4.3 – Условное графическое обозначение четырехразрядного компаратора двоичных чисел

Компаратор имеет две группы входов. На одну из них поступают разряды числа А, на другую группу – разряды числа В.

Появление единичного сигнала на одном из трех выходов компаратора фиксирует результат сравнения. Эти соотношения используются как логические условия (признаки) в микропрограммах, в устройствах автоматического контроля и диагностики и т.д.

В таблице 4.2 показана связь между сигналами на выходах и входах компаратора при сравнении одноразрядных чисел a_i и b_i, которые могут быть равны единице или нулю. На соответствующем выходе появляется единичный сигнал, когда в должном соотношении находятся коды на входах. Например, если a_i = 1, b_i = 1 (числа одинаковы), то функция, характеризующая равенство чисел, F_A=B = 1, а функции, характеризующие их неравенство, F_A<B = 0 и F_A>B = 0. Аналогично заполняются другие строки таблицы.

 

Таблица 4.2 – Таблица истинности одноразрядного компаратора

 

Логические аргументы	Логические функции
ai	bi	FA<B	FA=B	FA>B

 

По данным таблицы 4.2 запишем логические функции для одноразрядного компаратора в СДНФ:

(4.1)

.

 

Если значения a_i и b_i таковы, что правые части функций принимают единичные значения, то соотношения, указанные в индексах левых частей, выполняются. Если правые части функций принимают нулевые значения, то соотношения между a_i и b_i противоположны указанным.

Логическая схема одноразрядного компаратора, реализующая функции (4.1), приведена на рисунке 4.4.

 

Рисунок 4.4 – Логическая схема одноразрядного компаратора

 

Остановимся подробнее на равенстве чисел. Заметим, что функция F_A=B

функция «Равнозначность». По смыслу она противоположна функции F_A≠B «Неравнозначность»:

 

(4.2)

 

Поэтому проверку равенства одноименных разрядов двух чисел можно осуществить, используя логический элемент «Исключающее ИЛИ», дополненный инвертором (рисунок 4.5).

Когда цифры в одноименных разрядах чисел А и В одинаковы, то на выходах всех логических элементов «Исключающее ИЛИ» нулевые сигналы и функция F_A=B = 1. Если хотя бы в одной паре разрядов находятся разные цифры, то на выходе соответствующего логического элемента «Исключающее ИЛИ» единичный сигнал и функция F_A=B = 0, что указывает на неравенство чисел А и В.

 

 

Рисунок 4.5 – Логическая схема для проверки равенства двух многоразрядных двоичных чисел

 

Рассмотрим теперь неравенство чисел, используя выражение (4.1). Пусть А > В. Выявление такого неравенства начинается со старших разрядов; если они равны, то сравнивается следующая пара одноименных разрядов и т.д. Например, в случае трехразрядных чисел могут быть следующие варианты:

– неравенство цифр в старших разрядах (a₂ > b₂), что в соответствии с (4.1) представляется выражением . При этом неравенство чисел А > В описывается тем же выражением;

– равенство цифр в старших разрядах (a₂ = b₂), что представляется

выражением и неравенство цифр в средних разрядах (a₁ > b₁), что описывается выражением . При этом неравенство чисел А > В представляется конъюнкцией двух приведенных выражений ;

– равенство цифр в старших и средних разрядах (a₂ = b₂, a₁ = b₁), что описывается выражениям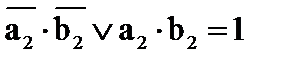и и , и неравенство цифр в младших разрядах (a₀ > b₀), что описывается выражением . При этом неравенство чисел А > В представляется конъюнкциями трех предыдущих выражений .

Поскольку возможен любой из трех вариантов, то выражение, учитывающее все варианты, запишется в виде дизъюнкций приведенных конъюнкций:

(4.3)

 

Если на выходе схемы (рисунок 4.6), элементы которой реализуют выражение (4.3), устанавливается единичный сигнал, то число А > B.

 

Рисунок 4.6 – Логическая схема для проверки неравенства двух

трехразрядных двоичных чисел

 

На рисунке 4.7 предыдущая схема дополнена логическим элементом «Исключающее ИЛИ–НЕ» (на входы которого подаются разряды a₀, b₀), конъюнктором (на выходе которого формируется функция F_A=B) и элементом ИЛИ–НЕ (на выходе которого формируется функция F_A<B). Если a₂ = b₂, a₁ = b₁, a₀ = b₀, то F_A=B = 1, т. е. число А = В. Если в результате сравнения чисел F_A>B = 0 и F_A=B = 0, то на выходе элемента ИЛИ–НЕ единичный сигнал (F_A<B = 1), т. е. число A < B.

 

 

Рисунок 4.7 – Логическая схема трехразрядного компаратора

 

По аналогичным схемам (см. рисунок 4.7) строятся компараторы для сравнения двоичных чисел с большей разрядностью.