Главная | Обратная связь

Назначение и принцип построения матричных умножителей двоичных чисел

 

Умножителем называется комбинационное цифровое устройство, формирующее на выходе число Q, равное произведению входных двоичных чисел A и B [9, 10].

Условное графическое обозначение (УГО) умножителя представляет собой прямоугольник с аббревиатурой MPL (от англ. Multiplier) во внутреннем поле (рисунок 1.3).

 

 

Рисунок 1.3 – Условное графическое обозначение умножителя

 

Предполагается, что числа A, B и Q представлены в двоичной позиционной системе счисления. При этом, если число A имеет n двоичных разрядов ( , ,…, ), число B имеет m двоичных разрядов ( 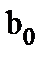, ,…, 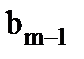), то для представления максимального значения произведения требуется n+m двоичных разрядов числа Q ( 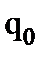, ,…, ). 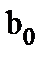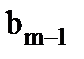Каждый разряд произведения является логической (переключательной) функцией аргументов , ,…, и , ,…, , значения которого можно найти из таблиц умножения либо путем выполнения умножения для заданных значений аргументов. Однако прямой логический синтез схемы умножителя, основанный на представлении функции выражениями в булевой алгебре, ввиду громоздкости неэффективен. Исключения составляют простейшие случаи перемножения одноразрядных или двухразрядных двоичных чисел. Поэтому на практике используют методы синтеза, основанные на разложении операции умножения на последовательность простейших арифметических действий с одноразрядными числами. Полагая, что в двоичном представлении значения чисел A и B определяются выражениями:

 

и (1.1)

 

произведение можно записать в форме двойной суммы:

 

(1.2)

 

Группируя члены с одинаковыми весовыми коэффициентами , преобразуем (2) к виду:

 

(1.3)

 

Из полученной формулы (1.3) видно, что для вычисления значения k-го разряда произведения необходимо выполнить совокупность произведений одноразрядных чисел ( , ), для которых сумма индексов i + j = k. Затем надо последовательно складывать эти произведения. При добавлении к сумме новых слагаемых возможно появление переноса в следующий k + 1-й разряд. Поэтому при нахождении k-го разряда произведения нужно к сумме членов ( , ) добавить все переносы, получаемые при сложении аналогичных членов для предыдущего k – 1 разряда.

Порядок, в котором производится сложение произведений ( ) и переносов из предыдущего разряда, значения не имеет.

Указанные действия мы выполняем, производя перемножение двоичных чисел на бумаге. Так, вычисляя произведение десятичных чисел [2]⁾ делаем следующую запись:

1 1 0 1

×

1 0 1 1

1 1 0 1

1 1 0 1

0 0 0 0

+

1 1 0 1

+

+

1 0 0 0 1 1 1 1

 

Штриховой линией обведены произведения ( ), для которых сумма индексов i + j = 4. В результате сложения этих произведений получаем значение 1. Однако после прибавления переноса из предыдущего третьего разряда четвертый разряд результата принимает значение 0 и формируется перенос в следующий пятый разряд .

Арифметическое перемножение одноразрядных чисел ( ) реализуется конъюнктором, поскольку логическое умножение совпадает с арифметическим.

В качестве элементарной ячейки умножителя используют устройство, показанное на рисунке 1.4, а.

 

 

Рисунок 1.4 – Элементарная ячейка умножителя. Логическая схема (а) и символическое обозначение (б)

 

Операция, реализуемая такой ячейкой, задается выражением ab + c + d, где a, b, c и d – одноразрядные двоичные числа. Результат, получаемый на выходе ячейки, представляется одноразрядной частичной суммой S и переносом C.

Из выражения (1.2) видно, что для нахождения произведения требуется получить mn одноразрядных произведений (a_ib_j), по одному для каждой возможной комбинации индексов i, j. Именно столько элементарных ячеек требуется для построения умножителя. Для наглядности представления структуры умножителя элементарные ячейки на структурной схеме целесообразно изображать в символической форме, как показано на рисунке 1.4, б. Поскольку такое обозначение содержит в явной форме сомножители a_i, b_j, участвующие в операции, реализуемой ячейкой, то связи, предназначенные для подведения к ячейкам этих сомножителей, можно на структурной схеме умножителя не обозначать.

Один из вариантов структурной схемы умножителя для m = n = 4 показан на рисунке 1.5.

D

 

Рисунок 1.5 – Умножитель четырехразрядных двоичных чисел.

Схема электрическая структурная

 

Каждый горизонтальный ряд элементарных ячеек выполняет умножение числа A на один из разрядов множителя B и суммирует полученное произведение с результатом аналогичной операции, реализуемой предыдущим (верхним) рядом. При этом частичная сумма с выходов элементарных ячеек верхнего ряда поступает на входы d элементарных ячеек следующего за ним ряда. Входы c использованы для приема переноса, возникающего при сложении произведений (a_ib_j).

В результате сдвига вправо элементов каждого следующего горизонтального ряда по отношению к предыдущему на одну позицию в каждом столбце элементов сумма индексов сомножителей a_i, b_j совпадает с номером к столбца и индексом разряда q_k произведения, формируемого в этом столбце.

На суммирующие входы d самого верхнего горизонтального ряда элементов и на входы переноса c крайних левых элементов в каждом ряду подают нули. При этом на выходах элементов верхнего ряда формируется (n + 1) – разрядная частичная сумма S₀ = Ab₀. Младший разряд частичной суммы S₀ является младшим разрядом q₀ произведения AB, поскольку других произведений, кроме a₀b₀, сумма индексов которых равна 0, нет. Более старшие разряды частичной суммы S₀ складываются во втором ряду элементарных ячеек с произведением Ab₁, формируя на выходах следующую частичную сумму S₁, младший разряд которой является вторым по старшинству разрядом произведения q₁. Аналогично формируются частичные суммы S₂, S₃, причем значение частичной суммы S₃ определяет старшие разряды произведения (q₃,…,q₇).

Умножитель, построенный по схеме на рисунке 1.5, можно использовать как секцию умножителя с более высокой разрядностью.

Для определения быстродействия умножителя следует вычислить суммарное время выполнения операции умножения, которое определяется длиной критического пути прохождения сигнала со входа на выход. Для простоты длина критического пути оценивается максимальным числом элементарных ячеек, которые сигнал должен пройти от входного нулевого разряда сомножителя до старшего разряда результата. Для схемы, показанной на рисунке 1.5, длина критического пути в общем случае составляет n + 2 (m - 1) и, следовательно, равна 10.

Таким образом, для определения суммарной задержки распространения сигнала в умножителе необходимо определить задержку распространения сигнала в элементарной ячейке и умножить на длину критического пути. Задержка распространения сигнала в элементарной ячейке умножителя определяется суммой среднего времени задержки распространения сигнала в конъюнкторе и одноразрядном сумматоре.

Исходя из вышесказанного, суммарное среднее время задержки распространения сигнала в умножителе можно определить по формуле.

 

T_{зд.р.ср.умн} = 10 (t_{зд.р.ср.кон} + t_{зд.р.ср.сум}), (1.4)

 

где t_{зд.р.ср.кон} – среднее время задержки распространения сигнала одного конъюнктора, нс;

t_{зд.р.ср.сум} – среднее время задержки распространения сигнала одноразрядного сумматора, нс.