 |
|
Каноническая форма одношаговых итерационных методов.
Итерационные методы решения СЛАУ
Общая характеристика итерационной схемы.
Суть итерационных методов для решения СЛАУ
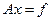, (1)
где 
имеет обратную, 
,
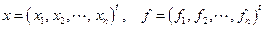состоит в выборе некоторого начального приближения 
к точному решению 
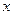и построению алгоритма последовательных приближений (итераций, от латинского слова “итерацио” – повторение) 
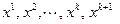(где k-номер итерации), таких, чтобы 
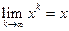. Приближение 
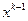выражается через известные предыдущие приближения по рекуррентной формуле
,
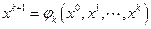где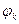 
- некоторая функция, зависящая, вообще говоря, от матрицы А, правой части f, номера итерации k.
Вычисление итераций продолжается до тех пор, пока не будет достигнута заданная точность, т.е. пока не будет выполнено условие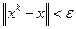 
.
Говорят, что итерационный метод имеет порядок m, если каждое последующее приближение зависит лишь от m предыдущих, т.е.
.
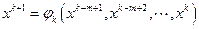Если 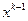вычисляется через одну предыдущую итерацию 
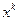- это одношаговый или двухслойный метод, если через 
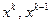- это двухшаговый или трехслойный метод.
Итерационные схемы высокого порядка при своей реализации требуют запоминания большого объема промежуточной информации и поэтому на практике ограничиваются значениям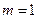и 
или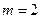 
.
От выбора функции 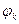зависит структура итерационной схемы. Если функция линейная, то итерационный метод называется также линейным.
Каноническая форма одношаговых итерационных методов.
Любой двухслойный итерационный метод можно записать в единой (канонической) форме
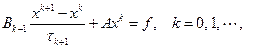, (2)
где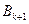 
- матрица, задающая тот или иной итерационный метод, 
- итерационные параметры,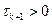 
, k – номер итерации. Предполагается, что задано начальное приближение и что существуют матрицы 
. Тогда из уравнения (2) можно последовательно определить все 
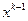. Для нахождения по известным 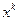и f достаточно решить систему уравнений
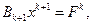(3)
где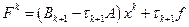 
.
Из уравнения (3) получается следующее выражение для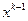
.
Матрица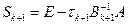 
называется матрицей перехода от n-ой итерации к (n+1)-ой итерации.
Если полученная таким образом последовательность 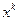сходится к некоторому пределу 
,то этот предел является точным решением системы (1). То есть, переходя к пределу в (2) при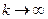 
получим 
.
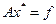Если 
, то метод запишется в виде
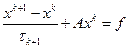(4)
и называется явным, т.к. 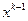находится по явной формуле
. (5)
Если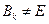 
метод (2) называется неявным, т.к. для определения 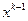надо решить уравнение (3).
Неявные итерационные методы следует применять лишь в том случае, если каждую матрицу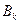 
легче обратить, чем исходную матрицу A (т.е. если решение системы с матрицей 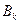требует меньше машинного времени или машинной памяти или алгоритмически проще, чем решение исходной задачи).
В общем случае 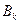и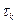 
могут зависеть от номера итерации k. Если 
и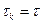 
, т.е. не зависят от номера итерации, то итерационный метод называется стационарным, и нестационарным - в противоположном случае.
Рассмотрим некоторые стационарные методы, т.е. методы в которых и 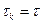.