 |
|
Метод простой итерации.
Если 
,то стационарный итерационный метод называется методом простой итерации и в матричном виде имеет вид
. (6)
В координатном виде он запишется в виде
.
Метод простой итерации является явной двухслойной схемой с постоянным параметром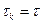 
. Матрица перехода имеет вид 
.
Метод Якоби.
Запишем систему (1) в виде
. (7)
Если 
и задано 
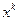- k-ое приближение к решению системы, то i-я компонента (k+1)-ого приближение вычисляется из i-го уравнения
. (8)
То есть
. 
. (10)
В выражении (10) слагаемое 
является i-ой компонентой столбца 
, где 
- диагональная матрица. Тогда (10) можно записать в виде
. (11)
Или в матричном виде
. (12)
Хотя формально эта схема неявная ( 
), но т.к. D – диагональная матрица, то получаются явные формулы.
Метод Зейделя.
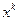Если и задано - k-ое приближение к решению системы, то в итерационном методе Зейделя i-я компонента (k+1)-ого приближение вычисляется из i-го уравнения, но при этом используются уже вычисленные компоненты 
(k+1)-ого приближения.
Используются два вида формул
, (13)
. (14)
Из формул (13) значения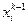 
вычисляются последовательно: 
, а из формул (14) 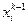вычисляются в обратном порядке.
Чтобы понять, как вычисляются значения 
запишем подробнее систему (13)
, (15)
, (16)
……………………………………
. (17)
Первая компонента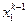 
вектора 
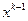находится из уравнения (15) явным образом, для ее вычисления нужно знать вектор 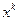и значение 
. При вычислении 
из уравнения (16) используется только что вычисленное значение 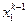и известные значения 
, с предыдущей итерации. Таким образом, компоненты 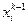вектора 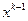вычисляются из уравнения (17) последовательно, начиная с i=1.
Запишем метод Зейделя в матричной форме. Для этого представим матрицу А в виде суммы трех матриц
,
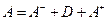где - диагональная матрица с той же главной диагональю, что и матрица А,
- нижняя треугольная (поддиагональная) матрица с нулями на главной диагонали ( 
),
- верхняя треугольная (наддиагональная) матрица с нулями на главной диагонали (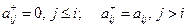 
).
Тогда уравнения (13) можно записать в виде
, (18)
или
(19)
Здесь 
- треугольная матрица и, следовательно, находятся по явным формулам.
- Метод верхней релаксации.
Обобщением метода Зейделя является метод верхней релаксации, который в матричном виде имеет вид
(20)
где 
- заданный числовой параметр.
Для получения расчетных формул перепишем (20) в виде
. (21)
В покомпонентной форме получим
.
Отсюда последовательно, начиная с i=1, находим все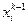
, (22)
, (23)
………………………………………………………….
. (24)