 |
|
Сходимость стационарных итерационных методов
Рассмотрим СЛАУ
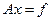 , (1)
, (1)
С невырожденной вещественной матрицей А и одношаговый стационарный итерационный метод, записанный в каноническом виде
 (2)
(2)
где  - задан.
- задан.
Решение системы (1) будем рассматривать как элемент n-мерного энергетического пространства  , порождаемого самосопряженным положительно определенным в H оператором D:
, порождаемого самосопряженным положительно определенным в H оператором D: 
 .
.
Смысл введения энергетического пространства  заключается в следующем. Как известно, последовательность элементов Н, сходящаяся в одной норме, сходится и в эквивалентной норме. Поэтому при исследовании сходимости конкретной итерационной схемы удобно выбрать такое энергетическое пространство
заключается в следующем. Как известно, последовательность элементов Н, сходящаяся в одной норме, сходится и в эквивалентной норме. Поэтому при исследовании сходимости конкретной итерационной схемы удобно выбрать такое энергетическое пространство  , в котором операторы итерационной схемы А и В обладали бы заданными свойствам, например были самосопряженными положительно определенными.
, в котором операторы итерационной схемы А и В обладали бы заданными свойствам, например были самосопряженными положительно определенными.
Перейдем к исследованию сходимости итерационного метода (2).Погрешность метода на n-ой итерации характеризуется вектором  , который согласно (1), (2) удовлетворяет однородному уравнению
, который согласно (1), (2) удовлетворяет однородному уравнению
 . (3)
. (3)
Говорят, что итерационный (2) метод сходится в энергетическом пространстве  , если
, если
 .
.
Т е о р е м а. Пусть А – симметричная положительно определенная матрица,  и выполнено условие
и выполнено условие
 . (4)
. (4)
Тогда итерационный процесс (2) сходится в энергетическом пространстве  , т.е.
, т.е.

со скоростью геометрической прогрессии  , где
, где  .
.
Д о к а з а т е л ь с т в о. Установим для погрешности  основное энергетическое тождество. Подставим в (3)
основное энергетическое тождество. Подставим в (3)  в виде
в виде

и получим
 . (5)
. (5)
Умножим (5) скалярно на

и, учитывая, что  т.е.
т.е. 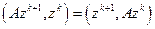 и
и
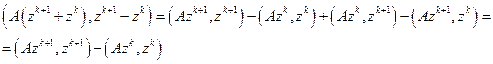
получим основное энергетическое тождество
 . (6)
. (6)
Пусть выполнено условие  . Тогда первое слагаемое в (6) не отрицательно и, следовательно,
. Тогда первое слагаемое в (6) не отрицательно и, следовательно,  . Поэтому последовательность
. Поэтому последовательность  невозрастающая и ограничена снизу нулем и в силу теоремы Вейерштрасса сходится при
невозрастающая и ограничена снизу нулем и в силу теоремы Вейерштрасса сходится при 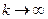 .
.
Докажем теперь, что  . Т.к.
. Т.к.  положительно определенный оператор, то существует такое число
положительно определенный оператор, то существует такое число  , что
, что
 .
.
Поэтому из (6) получим неравенство
 . (7)
. (7)
В силу сходимости последовательности  следует существование предела
следует существование предела
 . (8)
. (8)
Далее, из уравнения (3) находим
 ,
,  ,
,
 ,
,
 . (9)
. (9)
Отсюда и из (8) следует, что  .
.
Из (7) и (9) следует, что метод (2) сходится со скоростью геометрической прогрессии
 ,
,
где
 .
.