 |
|
Широко используются следующие два предела
НЕДЕЛЯ 6
Лекция 11
Функция. Предел функции.
Односторонние пределы функции
Пусть функция у=f(х) определена в некоторой окрестности точки х0. Тогда число А называется пределомфункции у=f(х) при х 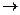 х0 (в точке х=х0), если для любого
х0 (в точке х=х0), если для любого  >0 существует
>0 существует  =
=  (
( 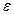 )>0, такое, что при 0 <|х—х0|<
)>0, такое, что при 0 <|х—х0|<  справедливо неравенство |f(х)-А|<
справедливо неравенство |f(х)-А|< 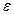 .
.
Если А – предел функции f(х) при х 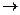 х0, то записывают это так
х0, то записывают это так
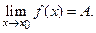
В самой точке х0функция f(х)может и не существовать (f(х0) не определено). Аналогично запись  обозначает, что для любого
обозначает, что для любого 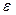 >0 существует N=N(
>0 существует N=N( 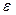 )>0, такое, что при |х|>N выполняется неравенство |f(х)-А|<
)>0, такое, что при |х|>N выполняется неравенство |f(х)-А|< 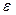 .
.
Если существует предел вида  , который обозначают также
, который обозначают также  или f(х0-0), то он называется пределом слева функции f(х)в точке x0. Аналогично если существует предел вида
или f(х0-0), то он называется пределом слева функции f(х)в точке x0. Аналогично если существует предел вида 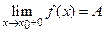 (в другой записи
(в другой записи 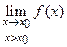 или f(x0+0)), то он называется пределом справафункции f(х)в точке x0. Пределы слева и справа называются односторонними. Для существования предела функции f(х)в точке x0необходимо и достаточно, чтобы оба односторонних предела в точке x0существовали и были равны, то есть f(x0-0)=f(x0+0).
или f(x0+0)), то он называется пределом справафункции f(х)в точке x0. Пределы слева и справа называются односторонними. Для существования предела функции f(х)в точке x0необходимо и достаточно, чтобы оба односторонних предела в точке x0существовали и были равны, то есть f(x0-0)=f(x0+0).
Основные теоремы о пределах.
Справедливы следующие основные теоремы о пределах.
Теорема 1. Пусть существуют 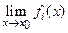 (i=1,…, п). Тогда
(i=1,…, п). Тогда

Теорема 2. Пусть существуют 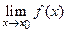 и
и  Тогда
Тогда
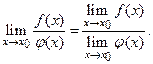
Эти утверждения сохраняются и при х0 =  .
.
Если условия этих теорем не выполняются, то могут возникнуть неопределенности вида 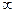 -
- 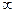 ,
,  ,
, 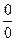 и др., которые в простейших случаях раскрываются с помощью алгебраических преобразований.
и др., которые в простейших случаях раскрываются с помощью алгебраических преобразований.
Замечательные пределы. Сравнение бесконечно малых функций.
Широко используются следующие два предела
1) 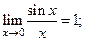
2) 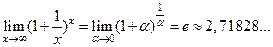 ,
,
которые называются соответственно первым и вторым замечательными пределами.
Если  (т. Е. для любого
(т. Е. для любого  >0 существует число
>0 существует число  >0, такое что при 0<
>0, такое что при 0< 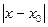 <
<  справедливо неравенство
справедливо неравенство 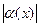 <
<  ), то
), то 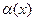 называется бесконечно малойфункцией или величиной при х
называется бесконечно малойфункцией или величиной при х 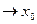 .
.
Для сравнения двух бесконечно малых функций 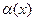 и
и 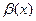 при х
при х 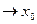 находят предел их отношения
находят предел их отношения
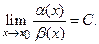 (1)
(1)
Если С 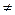 0, то
0, то 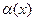 и
и 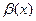 называются бесконечно малыми величинами одного и того же порядка;если С=0, то
называются бесконечно малыми величинами одного и того же порядка;если С=0, то 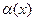 называется бесконечно малой более высокого порядка по сравнению с
называется бесконечно малой более высокого порядка по сравнению с 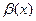 , а
, а 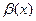 - бесконечно малой более низкого порядка по сравнению с
- бесконечно малой более низкого порядка по сравнению с 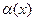 .
.
Если 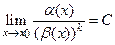 (0<
(0< 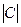 <
< 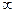 ),
),  то
то 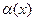 называется бесконечно малойпорядка k, по сравнению с
называется бесконечно малойпорядка k, по сравнению с 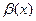 при х
при х 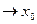 .
.
Если 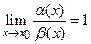 , то бесконечно малые
, то бесконечно малые 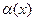 и
и 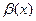 при х
при х 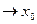 называются эквивалентными(равносильными) величинами и обозначают
называются эквивалентными(равносильными) величинами и обозначают 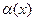 ~
~ 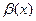 .
.
Например, при х 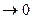
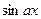 ~
~  ,
, 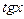 ~ х,
~ х,  ~ х,
~ х, 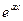 —1~
—1~  ..
..
Легко доказать, что предел отношения бесконечно малых функций 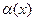 и
и 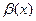 при х
при х 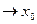 равен пределу отношения эквивалентных им бесконечно малых функций
равен пределу отношения эквивалентных им бесконечно малых функций 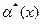 и
и 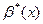 при х
при х 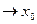 , т.е. верны предельные равенства
, т.е. верны предельные равенства
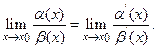
Литература: К.А. Хасеинов Каноны математики. Стр.130--146.
Лекция 12