Главная | Обратная связь

Непрерывность функции. Классификация

Точек разрыва функции.

Функция у=f(х)называется непрерывной при х=x₀ (в точке x₀), если:

1) функция f(х) определена в точке x₀и ее окрестности;

2) существует конечный предел функции f(х)в точке x₀;

3) этот предел равен значению функции в точке x₀, то есть

(2)

Если положить х=x₀+ , то условие непрерывности (2) будет равносильно условию

т. Е. функция у=f(х)непрерывна в точке x₀тогда и только тогда, когда бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции .

Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.

Точка x₀, в которой нарушено хотя бы одно из трех условий непре­рывности функции, называется точкой разрывафункции. Если в точке x₀существуют конечные пределы f(x₀-0) и f(x₀ +0), такие, что f(x₀-0) 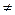f(x₀+0), то x₀называется точкой разрыва первого рода. Если хотя бы один из пределов f(x₀-0) и f(x₀+0) не существует или равен бесконечности, то точку x₀называют точкой разрыва второго рода. Если f(x₀-0)=f(x₀ +0) и функция f(х)не определена в точке x₀, то точку x₀называют устранимой точкой разрыва функции.

Свойства непрерывных функций:

1. Сумма, произведение и частное двух непрерывных функций есть непрерывная функция (при условии, что знаменатель отличен от нуля).

2. Пусть функция непрерывна в точке , а функция непрерывна в точке . Тогда сложная функция 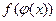непрерывна в точке .

3. Теорема 1 (Вейерштрасса). Если функция непрерывна на отрезке, то она ограничена на этом отрезке.

4. Теорема 2 (Вейерштрасса). Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значения.

5. Теорема 1 (Больцано-Коши). Если функция непрерывна на отрезке и на его концах принимает значения разных знаков, то внутри отрезка найдется хотя бы одна точка c, в которой данная функция обращается в ноль.

Литература: К.А. Хасеинов Каноны математики. Стр.146-155