 |
|
ОБРАЗЕЦ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
Задание 1.
Найти область определения функции  .
.
Решение.
Функция  существует на всей числовой оси
существует на всей числовой оси  , так как при любом значении
, так как при любом значении  функция имеет определенное вещественное значение. Точек разрыва нет, поэтому интервал непрерывности совпадает с областью определения функции
функция имеет определенное вещественное значение. Точек разрыва нет, поэтому интервал непрерывности совпадает с областью определения функции  .
.
Задание 3.
1.Найти производные функций указанного порядка:
а)  ,
, 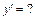 ;
;
б)  ,
,  ,
, 
Решение.
а)Применим правило дифференцирования суммы  , тогда
, тогда
 .
.
При дифференцировании первого слагаемого используем формулу  , где
, где  – константа. Получим:
– константа. Получим:
 .
.
Для второго слагаемого применим формулу  . Тогда
. Тогда

 .
.
Итак, в результате получим:
 .
.
б)Замечая, что  является сложной функцией
является сложной функцией  , где
, где  , применим правило дифференцирования сложной функции
, применим правило дифференцирования сложной функции  . Получим:
. Получим:
 .
.
Итак, в ответе получаем 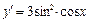 .
.
Найдем  . Так как
. Так как  , то
, то  . Применим формулу для вычисления производной произведения:
. Применим формулу для вычисления производной произведения:  , полагая
, полагая  , а
, а  . Таким образом
. Таким образом  . Как и выше, заметим, что
. Как и выше, заметим, что 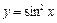 – сложная функция
– сложная функция  , где
, где  , поэтому
, поэтому  , а так как
, а так как 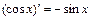 , имеем:
, имеем:
 .
.
Итак,  .
.
Задание 4.
- Найти
 .
.
Решение.

 .
.
Пояснения к решению:
1) В числителе применили формулу сокращенного умножения  .
.
2) Поделив почленно числитель на знаменатель, представили подынтегральную функцию в виде суммы более простых функций.
3) Применили свойства неопределенного интеграла: интеграл от суммы функций равен сумме интегралов от каждой функции, а также вынесли постоянный множитель за знак интеграла.
4) Использовали таблицу основных интегралов.
2.Найти  .
.
Решение.
В этом интеграле надо сделать замену переменных.
 .
.
Пояснения к решению:
1) Делаем замену переменных  . В прямых скобках показано, почему делается именно такая замена. В остальных строках приведены вспомогательные выкладки.
. В прямых скобках показано, почему делается именно такая замена. В остальных строках приведены вспомогательные выкладки.
2) Снова делаем замену переменных, возвращаясь к прежней переменной 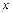 .
.
4.Найти 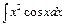 .
.
Решение.
В этом случае необходимо применить формулу интегрирования по частям  .
.


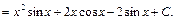
Пояснения к решению:
1) Применили формулу интегрирования по частям. Это дало возможность понизить показатель степени степенной функции.
2) Еще раз применили формулу интегрирования по частям.
Задание 5.
Вычислим интеграл  , используя метод замены переменно
, используя метод замены переменно

 .
.
Ответ: 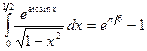 .
.
Задание 6.
а) Вычислить площадь фигуры, ограниченной линиями:
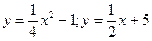 .
.
Решение. Построим фигуру, площадь которой требуется найти (рис. 2).
Графиком функции 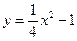 является парабола, ветви которой направлены вверх, так как
является парабола, ветви которой направлены вверх, так как  , а вершина находится в точке
, а вершина находится в точке  , где
, где
 ;
;  .
.
Таким образом,  .
.
Найдём точки пересечения параболы с осью  :
:
 ;
;  ;
;
 ;
;
 .
.
Парабола пересекает ось абсцисс в точках 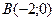 и
и  .
.
Для построения прямой, заданной уравнением  , достаточно указать координаты двух её точек:
, достаточно указать координаты двух её точек:

| ||

|
Найдём точку пересечения прямой и параболы. Для этого решим совместно систему уравнений:


Рис. 2
Итак, прямая пересекает параболу в точках  и
и  .Площадь заштрихованной фигуры
.Площадь заштрихованной фигуры  найдём по формуле
найдём по формуле
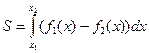 ,
,
где
 ,
,  ,
,  ,
,  ,
,
так как прямая является верхней границей заштрихованной области, а парабола − нижней.
Итак,

Ответ:Площадь фигуры, ограниченной линиями 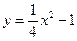 и
и  , равна
, равна  кв. ед.
кв. ед.
б) Вычислить объём тела, образованного вращением вокруг оси  фигуры, ограниченной линиями:
фигуры, ограниченной линиями:  ,
,  .
.


Решение.Объём тела, образованного вращением вокруг оси  фигуры, ограниченной кривой
фигуры, ограниченной кривой  , определяется по формуле:
, определяется по формуле:
 ,
,
.
Выразим  через
через  в уравнениях заданных кривых:
в уравнениях заданных кривых:
 ,
,  . Решая систему уравнений
. Решая систему уравнений 
получим пределы интегрирования  и
и  .
.
Тогда

Ответ:Объём тела, образованного вращением вокруг оси  фигуры, ограниченной линиями
фигуры, ограниченной линиями  ,
,  равен 0,47
равен 0,47  куб. ед.
куб. ед.
Задание 7.
Найти общее решение уравнения 
Решение.
Разделив в этом уравнении переменные и интегрируя обе части, получим


Ответ: 
Задача 8.
Группа студентов в течении недели осуществляет дежурство на 8 различных объектах. Сколькими способами можно составить расписание дежурств в субботу, если в этот день недели должно осуществляться дежурство только на 3 любых объектах?
Решение.Количество вариантов дежурств на объектах в субботу равно числу размещений из восьми элементов по три элемента. Находим  = 8*(8–1)*(8–2) = 8*7*6 =336.
= 8*(8–1)*(8–2) = 8*7*6 =336.
Ответ: Можно составить 336 различных вариантов дежурств на субботу на объектах.
Задача 9.
В полученной партии из 20 коробок лекарственных средств 5 коробок содержат брак. Для быстрого выяснения наличия брака в партии случайным образом вскрывают и обследуют 2 коробки. а) Найти вероятность того, что среди них окажется хотя бы одна браком. б) Найти вероятность этого же события, если обследовать 6 коробок.
Решение. Обозначим через Аi событие, состоящее в том, что i-ая извлеченная коробка окажется с браком; через А – хотя бы одна из коробок содержит брак. Тогда  – ни одна из коробок не содержит брак.
– ни одна из коробок не содержит брак.
а) Чтобы наступило событие  необходимо, чтоб наступили одновременно события
необходимо, чтоб наступили одновременно события  ,
,  , т.е.
, т.е.  =
=  ×
×  . Тогда по теореме умножения вероятностей [P(A×B)=P(A)×P(B|A)] получим
. Тогда по теореме умножения вероятностей [P(A×B)=P(A)×P(B|A)] получим
P(  )=P(
)=P(  ×
×  )=P(
)=P(  )×P(
)×P(  |
|  )=
)=  =0,553,
=0,553,
где  – вероятность того, что в первой коробке не будет брака;
– вероятность того, что в первой коробке не будет брака;  – того, что во второй тоже не будет брака при условии, что в первой его не было. Итак
– того, что во второй тоже не будет брака при условии, что в первой его не было. Итак
P(А)=1-P(  )=1–0,553=0,447,
)=1–0,553=0,447,
т.е. при таком способе проверки мы обнаружим брак в 45% случаев.
б) Чтобы наступило событие  необходимо, чтоб наступили одновременно события
необходимо, чтоб наступили одновременно события  ,
,  ,...,
,..., 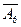 т.е.
т.е.  =
=  ×
×  ×...×
×...× 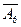 . Тогда по теореме умножения вероятностей [P(A×B)=P(A)×P(B|A)] получим
. Тогда по теореме умножения вероятностей [P(A×B)=P(A)×P(B|A)] получим
P(  )=P(
)=P(  ×
×  ×...×
×...× 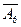 )=P(
)=P(  )×P(
)×P(  |
|  )×...×P(
)×...×P( 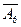 |
|  ×...×
×...×  )= =
)= =  ×
×  ×
×  ×
× 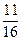 =0,129.
=0,129.
Итак , P(А)=1-P(  )=1–0,129=0,871,
)=1–0,129=0,871,
т.е. при таком способе проверки мы обнаружим брак в 87% случаев.
Ответ: а) 0,447; б) 0,871.
Задача 10.
На следующий год в местности Х прогнозируют две вспышки гриппа. Причем в весенней вспышке заболевают 5%, а в осенне-зимней – 10% людей данной возрастной группы. Считая, что эти вспышки вызываются различными возбудителями (т.е. заболевания в эти периоды независимы) оценить вероятность того, что случайно взятый человек в следующем году переболеет гриппом хотя бы 1 раз.
Решение.
Обозначим через А событие, состоящее в том, что случайно взятый человек заболеет гриппом весной, через В –осенью, через С – переболеет гриппом хотя бы 1 раз. Тогда С=А+В. По теореме [P(A+B)=P(A)+P(B)-P(AB)] о вероятности суммы двух событий и по теореме [P(AB)= P(A)×P(B)] о вероятности произведения двух независимых событий получим:
P(С)=P(A+B)=P(A)+P(B)- P(A)×P(B)=
=0,05+0,10-0,05×0,10=0,145,
т.е. 14,5% людей переболеют в этом году гриппом хотя бы 1 раз.
Ответ: 0,145.
Задача 11.
Молодожёны планируют, что у них будет 3 дочки и 2 сына. Считая, что у них действительно будет 5 детей найти шанс осуществления их желания, если вероятность рождения девочки 49%.
Решение.
Обозначим через А событие (успех), состоящее в том, что при данной беременности родится девочка. Тогда супружеская пара проводит 5 независимых «испытаний». Нас интересует событие, состоящее в наступлении ровно трёх успехов, и двух неуспехов. Воспользуемся формулой Бернулли наступления ровно m успехов в серии из n испытаний:
 ,
,
где p вероятность успеха в одном испытании. Итак, вероятность искомого события:
 =
= 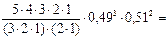 0,30601
0,30601
Ответ: вероятность этого события 30%.
Задача 12.
Вероятность заболевания гепатитом для жителя некоторой области в определённый период года составляет 5×10-4. Найти вероятность того, что среди 10000 обследованных жителей ровно 5 окажутся заболевшими.
Решение.
Вероятность успеха в одном испытании очень мала (р=0,0005), а количество испытаний велико (n=10000). Поэтому воспользоваться формулой Бернулли для вычисления вероятности наступления ровно m=5 успехов сложно с точки зрения громоздкости вычислений. Воспользуемся асимптотической формулой Пуассона
 , где m=p×n.
, где m=p×n.
Тогда m=0,0005×10000=5. И искомая вероятность равна
 0,17547
0,17547
Ответ: в 18% таких групп жителей будет ровно по 5 заболевших.
Задание 13.
Имеются 3 конверта. В первом конверте 25 контрольных работ по информатике; во втором – 10 контрольных работ по информатике и 5 контрольных работ по математике; в третьем – 15 контрольных работ по математике. Из выбранного наугад конверта вынули контрольную работу по информатике. Найти вероятность того, что контрольная работа взята из первого конверта (событие A).
Решение.
Из условия задачи, имеем:  – событие, выбор первого конверта;
– событие, выбор первого конверта;  – событие, выбор второго конверта;
– событие, выбор второго конверта;  – событие, выбор третьего конверта.Так как выбор каждого конверта равновероятен, то имеем:
– событие, выбор третьего конверта.Так как выбор каждого конверта равновероятен, то имеем:
 .
.
Соответственно вероятность выбора контрольных работ из первого, второго, третьего конвертов равна: 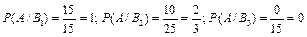 .
.
Тогда вероятность выбора контрольных работ из первого конверта равна:
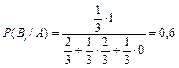
Ответ: вероятность выбора контрольной работы из первого конверта, равна 0,6.
Задание 14.
У 10 человек продолжительность инкубационного периода вирусного гепатита составила: 16, 20, 21, 15, 33, 39, 24, 24, 33, 39.
Требуется составить статистическое распределение и определить:
– математическое ожидание,
–дисперсию,
–среднеквадратическое отклонение.
Решение.
Составим статистическое распределение:
| xi | |||||||
| ni |
1. Найдем математическое ожидание по формуле:

2. Найдем дисперсию СВ по формуле:
 3. Найдем среднеквадратическое отклонение СВ по формуле:
3. Найдем среднеквадратическое отклонение СВ по формуле:

Задание 15.
Налоговый инспектор, изучая зависимость выработки  (ус.ед.) на одного работника от величины товарооборота магазина
(ус.ед.) на одного работника от величины товарооборота магазина  (ус.ед.) за отчётный период обследовал десять магазинов и получил следующие данные.
(ус.ед.) за отчётный период обследовал десять магазинов и получил следующие данные.

| ||||||||||

|
Полагая, что между признаками  и
и  имеет место линейная корреляционная связь, определить выборочное уравнение линейной корреляции. Построить диаграмму рассеяния и линию регрессии. Сделать вывод о направлении и тесноте связи между
имеет место линейная корреляционная связь, определить выборочное уравнение линейной корреляции. Построить диаграмму рассеяния и линию регрессии. Сделать вывод о направлении и тесноте связи между  и
и  . Используя полученное уравнение линейной регрессии, оценить
. Используя полученное уравнение линейной регрессии, оценить  (ус. ед.)
(ус. ед.)
Решение.
Для вычисления параметров а и b составим расчетную таблицу:
| N | 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|
Составляем систему:


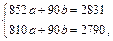




Уравнение регрессии У на Х имеет вид:  .
.
Построим диаграмму рассеяния и линию регрессии:

Точки  и
и  находим из уравнения регрессии.
находим из уравнения регрессии.




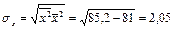 ,
,
 .
.
Найдем коэффициент корреляции по формуле:
 .
.
 корреляция положительная, то есть с возрастанием Х возрастает и У. Теснота связи достаточно большая, так как 0,93
корреляция положительная, то есть с возрастанием Х возрастает и У. Теснота связи достаточно большая, так как 0,93  1.
1.
Зная уравнение регрессии, можно вычислить предполагаемую выработки на одного работника при величине товарооборота магазина 35 ус. ед.
 (ус. ед.).
(ус. ед.).
Ответ: при величине товарооборота магазина 35 ус. ед. выработки на одного работника составит 56 ус. ед.