 |
|
Производная. Правила и формулы дифференцирования.
НЕДЕЛЯ 7
Лекция 13.
Производная. Правила и формулы дифференцирования.
Напомним, что приращением функции у=f(х) называется разность  , где
, где 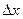 - приращение аргумента х.
- приращение аргумента х.
Из рисунка видно, что  (1).
(1).
Предел отношения приращения функции 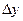 к приращению аргумента
к приращению аргумента 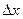 при произвольном стремлении
при произвольном стремлении 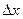 кнулю называется производной функции у=f(х)в точкех и обозначается одним из следующих символов: у', f'(х),
кнулю называется производной функции у=f(х)в точкех и обозначается одним из следующих символов: у', f'(х), 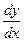 .
.

Рис. 1.
Таким образом, по определению
 (2)
(2)
Если указанный в формуле (2) предел существует, то функцию f(х)называют дифференцируемой в точке х,а операцию нахождения производной у' –дифференцированием.
Из равенства (1) и определения производной, (см. формулу (2)) следует, что производная в точке х равна тангенсу угла  наклона касательной, проведенной в точке М(х, у), к графику функции у=f(х) (см. рис. 1).
наклона касательной, проведенной в точке М(х, у), к графику функции у=f(х) (см. рис. 1).
Легко показать, что с физической точки зрения производная у'=f'(х) определяет скорость изменения функции в точке х относительно аргумента х.
Если С — постоянное число и и=и(х), v=v(x) – некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
1) (С)'=0;
2) (х)'.=1;
3) (и 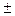 v)'=и'
v)'=и' 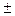 v';
v';
4) (С и)'=С и'
5)(и v)'=и' v+иv';
6)  ;
;
7)  ;
;
8) если у=f(и)и u= 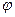 (х), т. Е. y=f(
(х), т. Е. y=f( 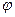 (x)) – сложная функция, составленная из дифференцируемых функций, то
(x)) – сложная функция, составленная из дифференцируемых функций, то
 или
или 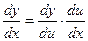 ;
;
9) если для функции у=f(х) существует обратная дифференцируемая функция х=g(у) и 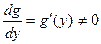 , то f'(х) =
, то f'(х) =  .
.
На основании определения производной и правил дифференцирования можно составить таблицу производных основных элементарных функций:
1) 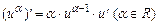
| 2) (  )' = )' =  lnа•u' lnа•u'
|
| 3) (еu)'=еu u' | 4) 
|
5) 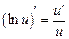
| 6) (sin u)’= соs uu’ |
| 7) (соs u)’=-sin u u’ | 8) 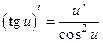
|
9) 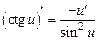 ; ;
| 10) (arcsin u)'= 
|
11) 
| 12) 
|
13) 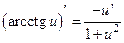
|
Уравнение касательной к кривой у=f(х) в точке Мо(х0; f(х0))
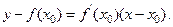
Уравнение нормалик кривой у=f(х)в точке Мо(х0; f(х0)):

При f/(х0)=0 уравнение нормали имеет вид х=х0.
Углом между кривыми в точке их пересеченияназывают угол между касательными к кривым в этой точке.
Логарифмической производной функции у=f(х)называется производная от логарифма этой функции, т. Е.
(ln f(x))’=f’(x)/f(x).
Последовательное применение логарифмирования и дифференцирования функций называют логарифмическим дифференцированием. В некоторых случаях предварительное логарифмирование функции упрощает нахождение ее производной. Например, при нахождении производной функции у=иv, где и=u(х), v=v(х), предварительное логарифмирование приводит к формуле
у =иv ln и v' + v и v-1 и'.
Если зависимость между переменными у и х задана в неявном виде уравнением F(х, у)=0, то для нахождения производной у'= 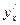 в простейших случаях достаточно продифференцировать обе части уравнения F(х, у)=0, считая у функцией от х, и из полученного уравнения, линейного относительно у', найти производную.
в простейших случаях достаточно продифференцировать обе части уравнения F(х, у)=0, считая у функцией от х, и из полученного уравнения, линейного относительно у', найти производную.
Литература: К.А. Хасеинов Каноны математики. Стр.155-167
Лекция 14.