 |
|
Условия применения рядов Тейлора.
16-17.
Степенной ряд есть функциональный ряд с общим членом fn (y) = an( y – y0 )n (n = 0, 1, 2, …) (an — действительные числа):
 an( y – y0 )n = a0 + a1( y – y0 ) + a2( y – y0 )2 + … + an( y – y0 )n + …
an( y – y0 )n = a0 + a1( y – y0 ) + a2( y – y0 )2 + … + an( y – y0 )n + …
Действительное число y0 называется центром степенного ряда. Заменой переменного x = y – y0 этот степенной ряд преобразуется в степенной ряд
 an xn = a0 + a1 x + a2 x2 + … + an xn + …
an xn = a0 + a1 x + a2 x2 + … + an xn + …
с нулевым центром. В дальнейшем ограничимся исследованием рядов именно такого вида.
Существуют степенные ряды, которые
а) сходятся при всех x (всюду сходящиеся степенные ряды), например 
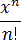 ;
;
б) сходятся только при x = 0, например  n! xn;
n! xn;
в) для некоторых x ≠ 0 сходятся, для других расходятся, например  xn.
xn.
Свойства степенных рядов.
- Если степенной ряд
 an xn сходится при x1, то он абсолютно сходится для всех x, удовлетворяющих неравенству | x | < | x1 |, а если степенной ряд расходится при x2, то он расходится и для всех х, удовлетворяющих неравенству | x | > | x2 |.
an xn сходится при x1, то он абсолютно сходится для всех x, удовлетворяющих неравенству | x | < | x1 |, а если степенной ряд расходится при x2, то он расходится и для всех х, удовлетворяющих неравенству | x | > | x2 |.
- Если степенной ряд
 an xn при некоторых x ≠ 0 сходится, а при остальных расходится, то существует, и притом только одно, положительное число r такое, что степенной ряд при | x | < r сходится, и даже абсолютно, а при | x | > r расходится. При x = r и x = – r ряд может как сходиться, так и расходиться. Число r называют радиусом сходимости степенного ряда. Если r > 0, то промежуток (– r, r) называется интервалом сходимости степенного ряда.
an xn при некоторых x ≠ 0 сходится, а при остальных расходится, то существует, и притом только одно, положительное число r такое, что степенной ряд при | x | < r сходится, и даже абсолютно, а при | x | > r расходится. При x = r и x = – r ряд может как сходиться, так и расходиться. Число r называют радиусом сходимости степенного ряда. Если r > 0, то промежуток (– r, r) называется интервалом сходимости степенного ряда.
Для вычисления радиуса сходимости используется теорема Коши – Адамара: радиус r сходимости ряда  an xn равен обратной величине верхнего предела последовательности {
an xn равен обратной величине верхнего предела последовательности { 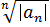 }:
}:
r = 
(при этом r = ∞, если 
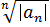 = 0, и r = 0, если
= 0, и r = 0, если 
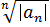 = ∞).
= ∞).
Верхний предел r числовой последовательности {bn} есть верхняя граница «сгущения» последовательности, т. е. для любого ε > 0 существует только конечное число индексов n таких, что bn > r + ε, но для бесконечного числа n справедливо неравенство bn > r – ε. Если для любого действительного числа C имеется бесконечное множество индексов n таких, что bn > C, то говорят, что верхний предел равен + ∞; если напротив, имеется только конечное число индексов n таких, что bn > C, то говорят, что верхний предел равен – ∞. Верхний предел существует всегда. Если существует 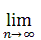
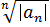 , то
, то

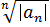 =
= 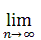
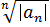 .
.
Радиус сходимости r степенного ряда  an xn может быть вычислен также при помощи признака Даламбера: если существует предел
an xn может быть вычислен также при помощи признака Даламбера: если существует предел 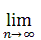
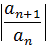 = q, то r =
= q, то r =  (r = ∞ при q = 0 и r = 0 при q = ∞).
(r = ∞ при q = 0 и r = 0 при q = ∞).
- В каждой внутренней точке интервала сходимости степенной ряд сходится абсолютно. Во всяком замкнутом промежутке, который целиком лежит в интервале сходимости, степенной ряд сходится равномерно. Если степенной ряд сходится при x = r (не обязательно абсолютно), то степенной ряд на [0 , r] сходится равномерно. (Если степенной ряд расходится при x = r, то на отрезке [0 , r] степенной ряд не может сходится равномерно.)
- Степенные ряды
 an xn и
an xn и 
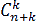 an + k xn (k = 0, 1, 2, …) имеют один и тот же радиус сходимости, однако в граничных точках интервала сходимости ряды могут иметь различное поведение.
an + k xn (k = 0, 1, 2, …) имеют один и тот же радиус сходимости, однако в граничных точках интервала сходимости ряды могут иметь различное поведение.
- Теорема единственности разложения в степенной ряд. Если два ряда
 an xn и
an xn и  bn xn сходятся в одном и том же интервале | x | < r и во всех его точках (или только в бесконечном подмножестве точек, имеющих нуль в качестве предельной точки) имеют одинаковые суммы, то эти суммы совпадают, т. е. an = bn для n = 0, 1, 2, …
bn xn сходятся в одном и том же интервале | x | < r и во всех его точках (или только в бесконечном подмножестве точек, имеющих нуль в качестве предельной точки) имеют одинаковые суммы, то эти суммы совпадают, т. е. an = bn для n = 0, 1, 2, …
- Если
 an( x – x0 )n — степенной ряд с радиусом сходимости r > 0, то его сумму f (x) можно разложить также в степенной ряд с центром в любой точке x1 из интервала сходимости:
an( x – x0 )n — степенной ряд с радиусом сходимости r > 0, то его сумму f (x) можно разложить также в степенной ряд с центром в любой точке x1 из интервала сходимости:
f (x) =  bn( x – x1 )n, где bn =
bn( x – x1 )n, где bn = 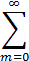
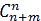 an + m( x – x1 )m.
an + m( x – x1 )m.
При этом все ряды, которые представляют bn, сходятся (см. свойство 4), а для радиуса сходимости r1 нового ряда справедливо неравенство
r1 ≥ r – | x – x0 |.
- а) Сумма f (x) степенного ряда
 an xn для всех значений x из интервала сходимости (– r, r) есть непрерывная функция. Если степенной ряд сходится при x = r, то сумма f (x) при этом значении x также непрерывна (слева):
an xn для всех значений x из интервала сходимости (– r, r) есть непрерывная функция. Если степенной ряд сходится при x = r, то сумма f (x) при этом значении x также непрерывна (слева):
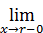 f (x) =
f (x) =  an rn.
an rn.
Если степенной ряд сходится при x = – r, то сумма f (x) при x = – r непрерывна справа (теорема Абеля о предельном значении).
б) Степенной ряд  an xn всегда можно почленно интегрировать на отрезке [0, x1], где | x1 | < r:
an xn всегда можно почленно интегрировать на отрезке [0, x1], где | x1 | < r:
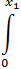 f (t) dt =
f (t) dt =  an
an 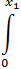 tn dt =
tn dt =  an
an 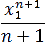 ;
;
при этом x1 может совпадать с одним из концов интервала сходимости, если степенной ряд сходится в этой точке.
в) Степенной ряд  an xn внутри его интервала сходимости можно почленно дифференцировать:
an xn внутри его интервала сходимости можно почленно дифференцировать:
f ' (x) =  an
an  =
=  n an xn – 1.
n an xn – 1.
Это утверждение верно также и для концов интервала сходимости, если ряд  n an xn – 1 сходится в этих точках. Степенной ряд внутри интервала сходимости можно дифференцировать любое число раз:
n an xn – 1 сходится в этих точках. Степенной ряд внутри интервала сходимости можно дифференцировать любое число раз:
f (k) (x) = 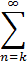
 an xn – k = k!
an xn – k = k! 
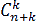 an + k xn.
an + k xn.
- Действия со степенными рядами.
а) Если f (x) =  an xn и g (x) =
an xn и g (x) =  bn xn, то для любого x, являющегося внутренней точкой интервалов сходимости обоих рядов, можно построить сходящиеся ряды
bn xn, то для любого x, являющегося внутренней точкой интервалов сходимости обоих рядов, можно построить сходящиеся ряды
f (x) ± g (x) =  (an ± bn) xn , f (x) · g (x) =
(an ± bn) xn , f (x) · g (x) = 
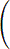
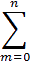 am bm – n
am bm – n  xn.
xn.
б) Пусть g (x) — сумма степенного ряда с радиусом сходимости r : g (x) =  bn xn, а f (u) — сумма степенного ряда с радиусом сходимости r' : f(u) =
bn xn, а f (u) — сумма степенного ряда с радиусом сходимости r' : f(u) =  an un. Тогда F (x) = f (g (x)) снова есть сумма некоторого степенного ряда: F (x) = cn xn — по крайней мере для тех x, для которых ряд
an un. Тогда F (x) = f (g (x)) снова есть сумма некоторого степенного ряда: F (x) = cn xn — по крайней мере для тех x, для которых ряд  |bn xn| сходится и имеет сумму, меньшую, чем r'. Коэффициенты cn вычисляются при помощи рядов: cn =
|bn xn| сходится и имеет сумму, меньшую, чем r'. Коэффициенты cn вычисляются при помощи рядов: cn = 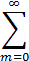 am bmn которые абсолютно сходятся при условии, что | b0 | < r', где (g (x))k =
am bmn которые абсолютно сходятся при условии, что | b0 | < r', где (g (x))k = 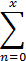 bkn xn. Другими словами, чтобы получить степенной ряд F (x), можно подставить u =
bkn xn. Другими словами, чтобы получить степенной ряд F (x), можно подставить u =  bnxn в степенной ряд
bnxn в степенной ряд  an un и привести подобные члены.
an un и привести подобные члены.
в) Если функция f (x) в окрестности нулевой точки есть сумма степенного ряда  an xn и f (0) – a0 ≠ 0, то функция
an xn и f (0) – a0 ≠ 0, то функция 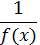 в окрестности нулевой точки есть сумма некоторого степенного ряда
в окрестности нулевой точки есть сумма некоторого степенного ряда  cn xn; так как для малых x оба ряда сходятся, то
cn xn; так как для малых x оба ряда сходятся, то
1 = 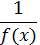 · f (x) =
· f (x) = 
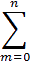 am cn – m
am cn – m  xn,
xn,
и согласно теореме о единственности разложения функции в степенной ряд выполняются соотношения
1 = a0 c0, 0 = 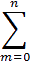 am cn – m при n ≥ 1;
am cn – m при n ≥ 1;
отсюда можно найти cn. Точно так же можно представить отношение двух функций g/f, являющихся суммами степенных рядов, как сумму степенного ряда  cn xn в некоторой окрестности нуля, если a0 = f (0) ≠ 0. Коэффициенты cn вычисляются из соотношения
cn xn в некоторой окрестности нуля, если a0 = f (0) ≠ 0. Коэффициенты cn вычисляются из соотношения
 =
=  cn xn
cn xn
или  bn xn =
bn xn = 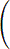
 an xn
an xn 
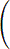
 cn xn
cn xn  ,
,
т. е. из системы bn = 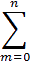 am cn – m для n = 0, 1, 2, …
am cn – m для n = 0, 1, 2, …
18.Ряд Тейлора в окрестности точки a имеет виды:
1) 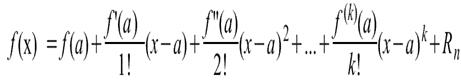 , где f(x) - функция, имеющая при х=а производные всех порядков. Rn - остаточный член в ряде Тейлора определяется выражением
, где f(x) - функция, имеющая при х=а производные всех порядков. Rn - остаточный член в ряде Тейлора определяется выражением 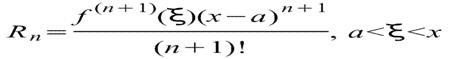
2) 
k-тый коэффициент (при хk) ряда определяется формулой
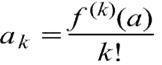
3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)
при a=0 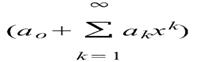
члены ряда определяются по формуле

Условия применения рядов Тейлора.
1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.