Главная | Обратная связь

Дифференциальное уравнение вида

или

называется дифференциальным уравнением с разделяющимися переменными.

Заметим, что в данных дифференциальных уравнениях каждая из функций зависит только от одной переменной, т.е. происходит разделение переменных.

Для решения такого дифференциального уравнения необходимо домножить или разделить обе части дифференциального уравнения на такое выражение, чтобы в одну часть уравнения входили только функции от и , в другую часть уравнения - только функции от , . Затем в полученном дифференциальном уравнении надо проинтегрировать обе части:

Следует заметить, что при делении обеих частей дифференциального уравнения на выражение, содержащее неизвестные и , могут быть потеряны решения, обращающие это выражение в ноль.

Обратим внимание, что дифференциальные уравнения с разделяющимися переменными легко сводятся к интегрированию. В общем случае получаем получаем дванеопределенных интеграла.

26. Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.

Чтобы численно решить уравнение методом простой итерации, его необходимо привести к следующей форме: , где 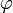— сжимающее отображение.

Для наилучшей сходимости метода в точке очередного приближения должно выполняться условие . Решение данного уравнения ищут в виде , тогда:

В предположении, что точка приближения «достаточно близка» к корню , и что заданная функция непрерывна , окончательная формула для такова:

С учётом этого функция определяется выражением:

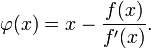
Эта функция в окрестности корня осуществляет сжимающее отображение^[1], и алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления: