 |
|
Интерполяция степенным рядом
Известно, что любую аналитическую функцию f(x) можно разложить в степенной ряд в окрестности некоторой точки x0.

По известному разложению легко вычислить значение полинома, составленного из первых k членов степенного ряда в заданной точке. В общем случае вопрос о выборе числа k для достижения необходимой точности вычислений совсем не прост. Стандартная практика завершать вычисление суммы, когда модуль последнего добавленного слагаемого в определенное число раз меньше модуля накопленной суммы. К счастью, часто используемые в вычислениях элементарные функции разложимы в ряд Тейлора, хотя, как будет показано ниже, и для таких функций метод интерполяции ограниченным степенным рядом не дает желаемых результатов.
Для разложения функции f(x) в ряд Тейлора в окрестности точки x0

cправедлива следующая оценка остаточного члена:
 ,
,
откуда можно найти число членов ряда, доставляющее необходимую точность приближения значения функции в точке х.
К недостаткам данного метода можно отнести наличие радиуса сходимости степенного ряда для разложения в окрестности точки x0. Обычно радиус сходимости степенного ряда известен заранее, и с этой проблемой справляются путем замены переменной, внося ошибки округления. Но, гораздо более коварная ситуация возникает со всюду сходящимися рядами, так как зачастую они сходятся настолько медленно, что становятся непригодными для вычислений. Кроме того, абсолютная ошибка вычислений по указанной формуле распределена неравномерно и нарастает по мере удаления от точки x0.
Определения
Рассмотрим систему несовпадающих точек 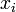 (
(  ) из некоторой области
) из некоторой области  . Пусть значения функции
. Пусть значения функции 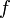 известны только в этих точках:
известны только в этих точках:

Задача интерполяции состоит в поиске такой функции 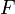 из заданного класса функций, что
из заданного класса функций, что

§ Точки 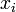 называют узлами интерполяции, а их совокупность — интерполяционной сеткой.
называют узлами интерполяции, а их совокупность — интерполяционной сеткой.
§ Пары  называют точками данных или базовыми точками.
называют точками данных или базовыми точками.
§ Разность между «соседними» значениями 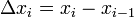 — шагом интерполяционной сетки. Он может быть как переменным так и постоянным.
— шагом интерполяционной сетки. Он может быть как переменным так и постоянным.
§ Функцию 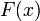 — интерполирующей функцией или интерполянтом.
— интерполирующей функцией или интерполянтом.
[править]Пример
1. Пусть мы имеем табличную функцию, наподобие описанной ниже, которая для нескольких значений  определяет соответствующие значения
определяет соответствующие значения 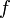 :
:

| 
|
| 0,8415 | |
| 0,9093 | |
| 0,1411 | |
| −0,7568 | |
| −0,9589 | |
| −0,2794 |
Интерполяция помогает нам узнать какое значение может иметь такая функция в точке, отличной от указанных, например, при x = 2,5?
К настоящему времени существует множество различных способов интерполяции. Выбор наиболее подходящего алгоритма зависит от ответов на вопросы: как точен выбираемый метод, каковы затраты на его использование, насколько гладкой является интерполяционная функция, какого количества точек данных она требует и т. п.
2. Найти промежуточное значение
| 15.5 | |
| ? | |
| 19.2 |

Формула Лагранжа
Интерполяционная формула Лагранжа обеспечивает построение алгебраического многочлена Pn(x) для произвольно заданных узлов интерполирования. Для n + 1 различных значений аргумента x0, x1, ..., xn и соответствующих значений функции f(x0) = y0,f(x1) = y1, ..., f(xn) = yn интерполяционная формула Лагранжа имеет вид,где х - значение аргумента функции, расположенного в интервале [x0, xn]. Необходимо отметить, что формула Лагранжа, в отличие от других интерполяционных формул, содержит явно yi(i=), что бывает иногда важно.