 |
|
Тема 5. Решение задач
Цель работы: проверка знаний и умений по темам предыдущих занятий.
Задания 1. Заданы множества А = {3, 7, 8, 9, 2}, B = {1, 5, 6, 7, 8, 9} и C = {1, 7, 18, 19, 12}. Какое из множеств имеет наибольшую мощность.
Задание 2. Заданы множества А = {-3, 2, 5, 9, 12} и B = {1, 5, 6, 7, 8, 9}. Задайте объединение, пересечение и разность множеств А и В.
Задание 3. На факультете филологии и журналистики учатся студенты, получающие стипендию, и студенты, не получающие стипендию. Пусть А – множество всех студентов факультета; В – множество студентов факультета, получающих стипендию. Укажите, что собой представляет объединение, пересечение и разность множеств А и В.
Задание 4. Пусть А – множество всех студентов-филологов университета; В – множество студентов первокурсников. Укажите, какие студенты содержатся во множестве А\В.
Задание 5. Сколькими способами можно отобрать 12 книг из 20 и расставить их в ряд на полке?
Задание 6. 20 человек знают английский и 10 - немецкий, из них 5 знают и английский, и немецкий. Сколько Человек всего?
Задание 7.Переплетчик должен переплести 14 различных книг в красный, зеленый и коричневые переплеты. Сколькими способами он может это сделать?
Задание 8. Сколькими способами 4 юноши могут пригласить четырех из шести девушек на танец?
Задание 9. У одного человека 7 книг по математике, а у второго – 9. Сколькими способами они могут обменять друг у друга две книги на две книги.
Задание 10. В кондитерском магазине продавались 4 сорта пирожных: эклеры, песочные, наполеоны и слоеные. Сколькими способами можно купить 7 пирожных.
Тема 6. ЗадачИ на графы
Цель работы: рассмотреть решение задач с использованием «Граф», проверить выполнение «Графов» на родословных.
Задача 1.
Утверждают, что в одной компании из пяти человек каждый знаком с двумя и только с двумя другими. Возможна ли такая компания?
Решение.
Каждого из этой компании изобразим на рисунке кружком. Если двое знакомы, соединим соответствующие кружки отрезком. Оказывается, что такие ситуации не только возможны, но все их можно описать аналогичными схемами (рис. 2.1). Из рассматриваемой компании нельзя выделить ни «четырехугольник», ни «треугольник», поскольку тогда из оставшихся нельзя будет составить компанию, удовлетворяющую условию, т. е. схема знакомства единственная.
Всякую схему, напоминающую многоугольник, принято называть циклом. (Древние греки «цикл» называли «колесом»; и действительно, на рисунке 2.2 изображено нечто, напоминающее колесо и с успехом заменяющее в рассматриваемой ситуации многоугольник.)
Что общего у схем, которые помогли нам решить задачи? Все они состоят из точек (кружков) и отрезков, соединяющих пары точек. Рассмотрение таких схем и приводит к понятию графа.
Граф представляет собой непустое множество точек и множество отрезков, оба конца которых принадлежат заданному множеству точек.
При изображении графов на рисунках или схемах отрезки могут быть прямолинейными или криволинейными; длины отрезков и расположение точек произвольны.
Все три фигуры на рисунке 2.3 изображают один и тот же граф.
С позиции теории графов нет различий между «мышкой» и «слоном» на рисунке 2.4.
Точки иначе называют вершинами, отрезки — ребрами графа. Вершины графа на рисунке выделяют обычно кружками или квадратикамихотя бы потому, что не всегда точки пересечения ребер принимаются за вершины графа. Например, по условию на рисунке 2.5 точка пересечения «диагоналей четырехугольника» вершиной не является.
Вершины, которые не принадлежат ни одному ребру, называются изолированными.
Обозначать вершины будем обычно заглавными буквами русского или латинского алфавитов и иногда числами. Ребра графа будем обозначать парами вершин или малыми буквами русского или латинского алфавитов.
Иногда мы будем изображать граф, не обозначая буквами его ребра и вершины.

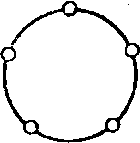

Рис. 2.1. Рис. 2.2. Рис. 2.3.


Рис. 2.4. Рис. 2.5.
Задача 2.
Как вы помните, охотник за мертвыми душами Павел Иванович Чичиков побывал у известных вам помещиков по одному разу у каждого. Он посещал их в следующем порядке: Манилова, Коробочку, Ноздрева, Собакевича, Плюшкина, Тентетникова, генерала Бетрищева, Петуха, Констанжогло, полковника Кошкарева. Найдена схема, на которой Чичиков набросал взаимное расположение имений и проселочных дорог, соединяющих их (рис. 1.1). Установите, какое имение кому принадлежит, если ни по одной из дорог Чичиков не проезжал более одного раза.
Задача 3.
