 |
|
Вероятность попадания в заданный интервал нормальной случайной величины
Как уже было установлено, вероятность того, что непрерывная случайная величина 
примет значение, принадлежащее интервалу 
, равна определенному интегралу от плотности распределения, взятому в соответствующих пределах:
.
Для нормально распределенной случайной величины соответственно получим:
.
Преобразуем последнее выражение, введя новую переменную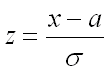 
. Следовательно, показатель степени выражения, стоящего под интегралом преобразуется в:
.
Для замены переменной в определенном интеграле еще необходимо заменить дифференциал и пределы интегрирования, предварительно выразив переменную из формулы замены:
;
;
– нижний предел интегрирования;
– верхний предел интегрирования;
(для нахождения пределов интегрирования по новой переменной 
в формулу замены переменной были подставлены 
и – 
пределы интегрирования по старой переменной 
).
Подставим все в последнюю из формул для нахождения вероятности:
где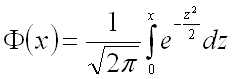 
– функция Лапласа.
Вывод: вероятность того, что нормально распределенная случайная величина примет значение, принадлежащее интервалу , равна:
,
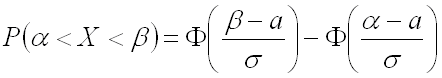где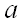 
– математическое ожидание, 
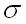– среднее квадратическое отклонение данной случайной величины.
Вопрос
Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины Х по абсолютной величине меньше заданного положительного числа d, т. е. требуется найти вероятность осуществления неравенства |x —а|<d.
Заменим это неравенство равносильным ему двойным неравенством
Тогда получим:
Приняв во внимание равенство:
(функция Лапласа—нечетная), окончательноимеем
Вероятность заданного отклонения равна
На рисунке наглядно показано, что если две случайные величины нормально распределены и а = 0, то вероятность принять значение, принадлежащее интервалу (-d,d),больше у той величины, которая имеет меньшее значение d. Этот факт полностью соответствует вероятностному смыслу параметра s .
Пример. Случайная величина Х распределена нормально. Математическое ожидание и среднее квадратическое отклонение Х соответственно равны 20 и 10. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех.
Решение: Воспользуемся формулой
По условию ,
тогда
Вопрос
Показательное распределение, распределение вероятностей на действительной прямой с плотностью вероятностей р (х), равной при х ³ 0 показательной функции le-lx, l > 0 [отсюда название П. р.] и при х<0 — нулю. Вероятность того, что случайная величина X, имеющая П. р., примет значения, превосходящие некоторое произвольное число х, будет при этом равна e-lx. П. р. является единственным непрерывным распределением вероятностей, обладающим тем свойством, что для любых значений x1 и x2 выполняется равенство
P(X>x1+x2)=P(X>x1) P(X>x2)
Роль, которую П. р. играет в задачах массового обслуживания теории, где предположение о П. р. времени обслуживания является естественным.
Вопрос
Центральная предельная теорема - общее название ряда предельных теорем теории вероятностей, указывающих условия, при выполнении к-рых суммы или другие функции от большого числа независимых или слабо зависимых случайных величин имеют распределения вероятностей, близкие кнормальному распределению.
В классич. варианте Ц. п. т. речь идет о последовательности
независимых случайных величин, имеющих конечные математич. ожидания 
и конечные дисперсии 
и о суммах
Пусть
Функции распределения
т. н. лнормированных
Вопрос
Правило 3-х Сигм
Преобразуем формулу
Введем обозначение
Тогда получим:
Если t=3, то
т. е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.
Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027=1-0,9973. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила трех сигм:
Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.
Вопрос
Математическая статистика
раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов. При этом статистическими данными называются сведения о числе объектов в какой-либо более или менее обширной совокупности, обладающих теми или иными признаками (таковы, например, данные таблиц 1а и 2а).