 |
|
СВОЙСТВА РАЗМЕЩЕНИЙ И ПЕРЕСТАНОВОК
КОМБИНАТОРИКА И ВЕРОЯТНОСТЬ
Учебное пособие для слушателей подготовительных курсов
Красноярск 2009
УДК 519
Рецензенты: Балашова О.Ю., канд. физ. - мат. наук, проф. каф. высшей математики СибГАУ
Пашковская О.В., канд. физ. - мат. наук, доц. каф. «Математика» КрИЖТ ИрГУПС
Печатается по решению методического совета ИИКТ
Новоселов Олег Вадимович
Скиба Людмила Петровна
Новоселов О.В. Комбинаторика и вероятность: учебн. пособие для слушателей подготовит. курсов / О. В. Новоселов, Л.П. Скиба. СибГАУ, Красноярск, 2009. – 78 с.
Настоящее учебное пособие предназначено для слушателей подготовительных курсов и абитуриентов. В пособии разобраны основные принципы и формулы классической комбинаторики, а также приведено большое число примеров. Кроме того, приведены примеры использования методов комбинаторики в теории вероятностей.
© Сибирский государственный аэрокосмический университет имени академика М.Ф. Решетнёва , 2009
ПРЕДИСЛОВИЕ
В настоящее время в связи с введением в школьный стандарт математического образования элементов комбинаторики и теории вероятностей, остро встают проблемы методической обеспеченности школьников и абитуриентов соответствующей литературой.
О необходимости изучения в школе элементов комбинаторики и теории вероятностей речь идет очень давно. Так ещё в 1899 году попечитель Московского учебного округа профессор П. А. Некрасов на совещании по вопросам о средней школе говорил об огромном значении в школьном образовании того, что сейчас принято называть стохастической линией в преподавании математики. Методические указания как раз и посвящены изложению тех понятий, фактов, задач и обстоятельств, с которых, собственно, берет свое начало эта самая стохастическая линия.
В школьном стандарте по математике перечисляются следующие вопросы комбинаторики и теории вероятностей.
«Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.
Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события».
Цель указаний: дать некоторый минимум, доступный слушателям подготовительных курсов и достаточный для формирования у них первоначальных комбинаторно-вероятностных представлений (в рамках школьного стандарта).
Главной целью изучения элементов комбинаторики является формирование специального типа мышления – комбинаторного, связанного с перебором и подсчетом числа конфигураций элементов, удовлетворяющих определенным условиям. Существенность развития комбинаторных возможностей интеллекта учащихся очевидна и с общих позиций теории развития личности, и с точки зрения различного рода практических приложений.
Знакомство с теорией вероятностей происходит в последних пяти параграфах. Собственно, никакой теории нет. Изложение ведется в рамках классического определения вероятности и, по существу, представляет собой практический полигон, на котором применяются полученные ранее комбинаторные навыки.
ВВЕДЕНИЕ
Когда кончается игра в три кости,
То проигравший снова их берет
И мечет их один в унылой злости.
Данте «Божественная комедия»
Комбинаторика – это раздел дискретной математики, посвященный решению задач выбора и расположения элементов в соответствии с каким-либо правилом. Например, сколькими способами можно выбрать 6 карт из колоды, состоящей из 36 карт; или сколькими способами можно составить очередь, состоящей из10 человек и т.д. Каждое правило в комбинаторике определяет способ построения некоторой конструкции, составленной из элементов исходного множества и называемой комбинацией. Основная цель комбинаторики состоит в подсчете количества комбинаций, которые можно составить из элементов исходного множества в соответствии с заданным правилом. Простейшими примерами комбинаторных конструкций являются перестановки, размещения и сочетания.
Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр или иных объектов. Например, начальнику цеха надо распределить несколько видов работ между имеющимися станками, агроному – разместить посевы сельскохозяйственных культур на нескольких полях, заведующему учебной частью школы – составить расписание уроков, лингвисту – учесть различные варианты значений букв незнакомого языка и т.д. Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов, называется комбинаторикой.
Теория вероятностей – это раздел математики, изучающий закономерности, присущие случайным явлениям. Казалось бы, «закономерность» и «случай» – противоположности. Закономерное – то, что в какой-то мере можно предсказать, случай же – как раз нечто непредсказуемое. Тем не менее, и случайным явлениям, не предсказуемым в полной мере, оказывается, могут быть присущи определенные закономерности, касающиеся большого числа однотипных случайных явлений, выполняющиеся приблизительно, в среднем.
В повседневной речи мы часто употребляем слова: «случайность», «случай» и другие. Например, мы говорим, что «это была случайность, что я завалил экзамен»; или «только случай помог кораблю вернуться в порт приписки после долгих странствий». В обыденном представлении случай противопоставляется закономерности, является чем-то, что нарушает ход событий. Но так ли это на самом деле? Если выучить только 5 вопросов из 25, то будет ли случайностью двойка на экзамене? Скорее закономерностью, хотя вероятность сдачи все-таки есть. Поэтому случайные события также подчиняются своим закономерностям. Изучение этих закономерностей и занимается наука о случайном – теория вероятностей.
Комбинаторика и теория вероятностей, подобно другим математическим наукам, развилась из потребностей практики.
Систематические исследования в области комбинаторики и теории вероятностей началось в XVI в. В жизни привилегированных слоёв тогдашнего общества большое место занимали азартные игры, широко были распространены всевозможные лотереи. В связи с этим, первые комбинаторные и вероятностные задачи касались в основном азартных игр – вопросов, сколькими способами можно выбросить данное число очков, бросая две или три кости, или сколькими способами можно получить двух королей в данной карточной игре, каковы шансы выиграть в той или иной ситуации. Но они навсегда остались бы салонными играми, если бы и в практической деятельности (например, в статистике населения) не пришлось решать схожих задач.
Возникновение теории вероятностей и комбинаторики как науки относится в середине XVII в. и связано с исследованиями Б. Паскаля (1623-1662), П. Ферма (1601-1665) и Х. Гюйгенса (1629-1695) в области теории азартных игр. В этих работах постепенно формировались такие важные понятия, как вероятность и математическое ожидание; были установлены свойства и приёмы их вычисления. Особенно большую роль здесь сыграла задача о разделе ставки, которую предложил Паскалю его друг шевалье де Мере, страстный игрок. Проблема состояла в следующем: «матч» в орлянку ведётся до шести выигранных партий; он был прерван, когда один игрок выиграл 5 партий, а другой – 4; как разделить ставку? Было ясно, что раздел в отношении 5:4 несправедлив. Применив методы комбинаторики, Паскаль решил эту задачу. Он рассуждал так:
«Предположим, что ставка каждого игрока составляет 32 червонца и что первому не хватает одной партии до выигрыша, а второму двух. Им предстоит сыграть еще одну партию. Если ее выиграет первый, он получит всю сумму, то есть 64 червонца; если второй, у каждого будет по две победы, шансы обоих станут равны, и в случае прекращения игры каждому, очевидно, надо дать поровну. Итак, если выиграет первый, он получит 64 червонца. Если выиграет второй, то первый получит лишь 32. Поэтому, если оба согласны не играть предстоящей партии, то первый вправе сказать: 32 червонца я получу во всяком случае, даже если я проиграю предстоящую партию, которую мы согласились признать последней. Стало быть, 32 червонца мои. Что касается остальных 32 – может быть, их выиграю я, может быть, и вы; поэтому разделим эту сомнительную сумму пополам. Итак, если игроки разойдутся, не сыграв последней партии, то первому надо дать 48 червонцев, или же 3/4 всей суммы, второму 16 червонцев, или 1/4, из чего видно, что шансы первого из них на выигрыш втрое больше, чем второго (а не вдвое, как можно было бы подумать при поверхностном рассуждении).»
Другое, более общее, решение дал Ферма. Эти труды Паскаля и Ферма, составившие основу теории вероятностей, одновременно содержали принципы определения числа комбинаций элементов конечного множества, устанавливая тем самым ставшую затем традиционной связь комбинаторики с теорией вероятностей.
Большой вклад в систематическое развитие комбинаторных методов был сделан Г. Лейбницем (1646-1716) в его диссертации «Комбинаторное искусство» (1666), где, по-видимому, впервые появился термин «комбинаторный». Большое значение для становления теории вероятностей и комбинаторики имела работа Я. Бернулли (1654-1706) «Искусство предположений» (1713), посвященная основным понятиям теории вероятностей, где обстоятельно изложен также и ряд комбинаторных понятий и указаны их применения для вычисления вероятностей. Можно считать, что с появлением работ Г. Лейбница и Я. Бернулли комбинаторные методы выделись в самостоятельную часть математики. С работы Бернулли по существу начинается становление теории вероятностей как науки. Доказанная им теорема, получившая впоследствии название «закона больших чисел», была первым теоретическим обоснованием накопленных ранее фактов.
Выдающаяся роль в развитии теории вероятностей принадлежит знаменитому математику П. Лаплас (1749-1827). Он впервые дал стройное и систематическое изложение основ теории вероятностей: «Аналитическая теория вероятностей» (1812). Он дал доказательство одной из форм центральной предельной теоремы (теоремы Муавра-Лапласа) и развил ряд замечательных приложений теории вероятностей к вопросам практики, в частности к анализу ошибок наблюдений и измерений.
В развитии теории вероятностей приняло участие огромное число замечательных учёных. Однако становление теории вероятностей как строгой математической науки, основанной на аксиоматическом методе, связано в первую очередь с выдающимся советским математиком А.Н. Колмогоровым (1903-1987). В 1933 г. вышла книга Колмогорова «Основные понятия теории вероятностей», в которой была предложена аксиоматика, получившая всеобщее признание и позволившая охватить не только все классические разделы теории вероятностей, но и дать строгую основу для развития её новых разделов, вызванных запросами естествознания.
Возрождение интереса к комбинаторике относится к 50-м годам XX в. Это связано с бурным развитием кибернетики и дискретной математики и широким использованием ЭВМ. В этот период активизировался интерес и к классическим комбинаторным задачам. Быстро выросло число комбинаторных задач и их разнообразие. Во многих областях математики (теория графов, теория чисел, теория групп, кибернетика, вычислительная математика и др.) имеются задачи или группы задач, комбинаторный характер которых угадывается без особых усилий.
В данных методических указаниях разбираются классические задачи и методы комбинаторики и теории вероятностей.
ПРИНЦИП УМНОЖЕНИЯ
При решении комбинаторных задач используются два правила: принцип умножения и принцип сложения.
Принцип умножения. Если элемент А можно выбрать из некоторого множества m способами и если после каждого такого выбора элемент B можно выбрать n способами, то пара элементов (А,В) в указанном порядке может быть выбрана (m×n) способами.
Пример 1.1. Из пункта А в пункт В ведут 3 дороги, а из пункта В в пункт С – 4 дороги. Сколькими способами можно совершить поездку из А в С через В?
Решение. В пункте А есть 3 способа выбора дороги в пункт В, а в пункте В есть 4 способа попасть в пункт С. Согласно принципу умножения, существует 3×4=12 способов попасть из пункта А в пункт С.
Принцип умножения легко обобщается на случай выбора трех и более элементов.
Пример 1.2. Сколько четырехзначных чисел можно составить из цифр 1, 2, 3, 4 и 5, если: а) цифры не повторяются; б) повторение допустимо; в) числа должны быть нечетные и без повторения.
Решение. а) Первую цифру можно выбирать 5-ю способами. Так как в числе цифры не повторяются, то вторую цифру уже можно выбрать из четырех оставшихся 4-мя способами. Далее получаем, что третью цифру можно выбрать 3-мя способами и четвертую – двумя. Таким образом, число возможных четырехзначных чисел равно N=5×4×3×2=120.
б) Так как повторения допустимы, то каждую цифру можно выбирать каждый раз из 5 имеющихся цифр, т.е. пятью способами. Тогда число возможных чисел равно N=5×5×5×5=54=625.
в) У нечетного числа последняя цифра нечетная, т.е. в данном случае может быть либо 1, либо 3, либо 5. Поэтому на это место можно поставить любую из этих трех чисел. После этого на оставшиеся места можно поставить: четыре цифры, три цифры и две цифры, ибо никакие из пяти цифр нельзя использовать более одного раза. Таким образом, N=3×4×3×2=72.
Упражнения
1.1. Имеется 5 видов конвертов без марок и 4 вида марки. Сколькими способами можно выбрать конверт и марку для посылки письма?
Ответ:  .
.
1.2. На вершину горы ведут пять дорог. Сколькими способами турист может подняться на гору и потом спуститься с неё? Решите ту же задачу при дополнительном условии, что подъём и спуск происходят по разным дорогам.
Ответ:  ;
;  .
.
1.3. При составлении одного варианта письменной контрольной работы по математике преподаватель располагает 4 задачами по геометрии, 8 – по алгебре и 3 – по тригонометрии. Сколькими способами можно составить этот вариант, если в него должно войти по одной задаче из перечисленных разделов?
Ответ:  .
.
1.4. Из двух полуфинальных групп, каждая их которых содержит по 6 команд, в финал выходит по одной команде. Сколько может быть различных вариантов участников финального матча?
Ответ: 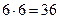 .
.
1.5. В книге из 20 страниц на каких-либо трех страницах надо поместить по одной разной иллюстрации. Сколькими способами это можно сделать?
Ответ:  .
.
1.6. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
Ответ:  .
.
1.7. Сколькими способами Чип и Дейл могут поделить между собой 5 разных орешков?
Ответ:  .
.
1.8. На складе имеются 6 ящиков с различными фруктами и 3 ящика с различными овощами. Сколькими способами можно каждой из двух овощных палаток выдать по одному ящику с фруктами и овощами?
Ответ:  .
.
ПРИНЦИП СЛОЖЕНИЯ
Принцип сложения. Если элемент А можно выбрать из некоторого множества m способами, а другой элемент B – n способами, причём выборы А и В таковы, что взаимно исключают друг друга и не могут быть выбраны одновременно, то выбор какого-либо одного из этих элементов (либо А, либо В) можно осуществить (m+n) способами.
В качестве иллюстрации данного принципа рассмотрим следующий простой пример.
Пример 2.1. Пусть из города A в город B можно добраться одним авиамаршрутом, двумя железнодорожными маршрутами и тремя автобусными маршрутами. Сколькими способами можно добраться из города A в город B?
Решение. Все условия принципа сложения здесь выполнены, поэтому, в соответствии с этим принципом, получим 1+2+3=6 способов.
Рассмотрим пример, иллюстрирующий различие принципов умножения и сложения.
Пример 2.2. В магазине электроники продаются три марки телевизоров и два вида видеомагнитофонов. У покупателя есть возможности приобрести либо телевизор, либо видеомагнитофон. Сколько способами он может совершить одну покупку? Сколько различных комплектов, содержащих телевизор и магнитофон, можно приобрести в этом магазине, если покупатель собирается приобрести в паре и телевизор, и видеомагнитофон?
Решение. Один телевизор можно выбрать тремя способами, а магнитофон – другими двумя способами. Тогда телевизор или магнитофон можно купить 3+2=5 способов.
Во втором случае один телевизор можно выбрать тремя способами, после этого видеомагнитофон можно выбрать двумя способами. Следовательно, в силу принципа умножения, купить телевизор и видеомагнитофон можно 3×2=6 способами.
Замечание. Обычно принцип сложения применяется в тех случаях, когда в задачах встречаются союзы «или», «либо, либо» (телевизор или видеомагнитофон), а принцип умножения – в задачах, содержащих союз «и» (телевизор и видеомагнитофон).
Рассмотрим теперь примеры, в которых применяются оба правила комбинаторики: и принцип умножения, и принцип сложения.
Пример 2.3. В корзине лежат 12 яблок и 10 апельсинов. Ваня выбирает либо яблоко, либо апельсин, после чего Надя выбирает из оставшихся фруктов и яблоко и апельсин. Сколько возможно таких выборов?
Решение. Ваня может выбрать яблоко 12 способами, апельсин – 10 способами. Если Ваня выбирает яблоко, то Надя может выбрать яблоко 11 способами, а апельсин – 10 способами. Если Ваня выбирает апельсин, то Надя может выбрать яблоко 12 способами, а апельсин – 9 способами. Таким образом, Ваня и Надя могут сделать свой выбор  способами.
способами.
Пример 2.4. Есть 3 письма, каждое из которых можно послать по 6 адресам. Сколькими способами это можно сделать?
Решение. В данной задаче мы должны рассмотреть три случая: а) все письма рассылаются по разным адресам, б) все письма посылаются по одному адресу, в) только два письма посылаются по одному адресу. Если все письма рассылаются по разным адресам, то число таких способов легко находится из принципа умножения: n1=6×5×4=120 способов. Если все письма посылаются по одному адресу, то таких способов будет n2=6. Таким образом, остается рассмотреть только третий случай, когда только 2 письма посылаются по одному адресу. Выбрать какое-либо письмо мы можем 3 способами и послать его по какому-либо выбранному адресу можем 6 способами. Оставшиеся два письма мы можем послать по оставшимся адресам 5 способами. Следовательно, послать только два письма по одному адресу мы можем n3=3×6×5=90 способами. Таким образом, разослать 3 письма по 6 адресам в соответствие с принципом сложения можно
n1+n2+n3 = 120+6+90 = 216 способами.
Упражнения
2.1. В урне содержится 3 синих, 5 красных и 2 белых шара. Сколькими способами можно вытащить из урны либо два белых шара, либо два цветных шара, из которых один синий, а другой – красный?
Ответ: Все шары различимы и порядок важен. Поэтому все способов 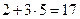 .
.
2.2. Имеется 6 различных конвертов без марок, 4 различные марки и 3 различных конверта с марками. Сколькими способами можно выбрать конверт с маркой для отправки письма?
Ответ:  .
.
2.3. Семья новоселов хочет приобрести письменный стол, книжный шкаф и диван. В мебельном магазине имеется 6 письменных столов, 4 книжных шкафа и 12 диванов, Кроме того, есть 2 гарнитура, содержащих письменный стол и диван, и 8 гарнитуров, содержащих книжный шкаф и письменный стол. Сколькими способами может быть сделана покупка?
Ответ:  .
.
2.4. В букинистическом магазине лежат 6 разных изданий романа И.С. Тургенева «Рудин», 3 издания его романа «Дворянское гнездо» и 4 издания романа «Отцы и дети». Кроме того, есть 5 разных сборников, в каждом из которых есть романы «Рудин» и «Дворянское гнездо», и 7 сборников с романами «Дворянское гнездо» и «Отцы и дети». Сколькими способами можно сделать покупку, содержащую по одному экземпляру каждого из этих романов?
А если в магазине есть ещё 3 сборника, содержащие романы «Рудин» и «Отцы и дети», и 5 книг, содержащих все три романа?
Решение: Можно купить либо по экземпляру каждого романа, либо сборник, содержащий два романа, и экземпляр третьего романа. Из принципов сложения и умножения получаем  способа. Во втором случае можно купить ещё сборник, содержащий романы «Рудин» и «Отцы и дети», и один экземпляр «Дворянского гнезда», либо сразу все романы. Всего имеем
способа. Во втором случае можно купить ещё сборник, содержащий романы «Рудин» и «Отцы и дети», и один экземпляр «Дворянского гнезда», либо сразу все романы. Всего имеем  способов.
способов.
При решении комбинаторных задач важно уметь выделять случаи, где можно использовать те или иные формулы. Пусть имеется множество, состоящее из n элементов, например, урна, содержащая n различных шаров. Выборкой будем называть любую совокупность k элементов этого множества; другими словами, выбор k шаров из урны. Однако при постановке такого эксперимента должно быть строго оговорено, каким способом производится выбор и что понимается под различными выборками.
Существует две принципиально различные схемы выбора. В первой схеме выбор осуществляется без возвращения элементов. Это означает, что в выборке невозможны повторения элементов. Во второй схеме выбор осуществляется поэлементно с обязательным возвращением отобранного элемента при каждом шаге. Это означает, что в выборке возможны повторения.
После того как выбор тем или иным способом осуществлен, отобранные элементы могут быть либо упорядочены, либо неупорядочены. В первом случае, выборки, состоящие из одних и тех же элементов, но отличающиеся порядком следования этих элементов, объявляются различными. Во втором случае порядок следования элементов не принимается во внимание, и такие выборки объявляются тождественными.
В результате получаются четыре различные постановки эксперимента по выбору k элементов из общего числа n элементов некоторого множества.
| Набор Выбор | Упорядоченный | Неупорядоченный |
| Без возвращений (без повторений) | Размещения

| Сочетания

|
| С возвращением (с повторениями) | Размещения с повторениями

| Сочетания с повторениями

|
Эту таблицу для случая n=3, k=2 можно записать следующим образом:
| Набор Выбор | Упорядоченный | Неупорядоченный |
| Без возвращений (без повторений) | (1,2) (1,3) (2,3) (2,1) (3,1) (3,2) | (1,2) (1,3) (2,3) |
| С возвращением (с повторениями) | (1,2) (2,1) (1,1) (1,3) (3,1) (2,2) (2,3) (3,2) (3,3) | (1,2) (1,3) (2,3) (1,1) (2,2) (3,3) |

 ФАКТОРИАЛ
ФАКТОРИАЛ
Для любого натурального числа n произведение  обозначается n! (читается «эн факториал»), т.е.
обозначается n! (читается «эн факториал»), т.е.

Считается, что 0!=1.
Пример 3.1. Вычислить
 .
.
Решение. Так как  и
и  , то
, то
 .
.
Поскольку
 и
и  ,
,
то
 .
.
Поэтому
 .
.
Пример 3.2. Упростить выражение
 (n³1).
(n³1).
Решение. Так как  и
и  , то
, то
 .
.
Пример 3.3. Решить уравнение
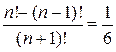 , где n³1.
, где n³1.
Решение. Так как  , то
, то
 .
.
Кроме того,  . Итак, исходное уравнение равносильно уравнению
. Итак, исходное уравнение равносильно уравнению
 .
.
Если n=1, то уравнение примет вид
 ,
,
т.е. получается противоречие 0=1/6, следовательно, n=1 не является решением уравнения. Если n³2, то уравнение примет вид
 ,
,
т.е.  . Отсюда получаем n1=2 и n2=3.
. Отсюда получаем n1=2 и n2=3.
Выражение n! означает, что перемножаются все натуральные числа подряд и наибольший из сомножителей равен n. Выражение n!! означает, что перемножаются натуральные числа через одно и наибольший сомножитель также равен n. Таким образом, если n чётное, то n!! есть произведение всех чётных чисел, не превышающих n (  ); если же n нечётное, то это произведение всех нечётных чисел, не превышающих n (
); если же n нечётное, то это произведение всех нечётных чисел, не превышающих n (  ). Аналогично, если после числа расположено три восклицательных знака, то перемножаются каждое третье число, а если четыре – каждое четвёртое. Например,
). Аналогично, если после числа расположено три восклицательных знака, то перемножаются каждое третье число, а если четыре – каждое четвёртое. Например,  .
.
Упражнения
3.1. Вычислить: а)  , б)
, б)  .
.
Ответ: а) 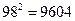 , б)
, б)  .
.
3.2. Упростить: а)  , б)
, б) 
Ответ: а)  , б) m+2.
, б) m+2.
3.3. Найти все натуральные n, удовлетворяющие условию  .
.
Ответ: 8.
3.4. В забеге участвуют 5 спортсменов. Сколькими способами могут распределиться места в результате забега?
Ответ:  .
.
РАЗМЕЩЕНИЯ
Пусть имеется некоторое множество, содержащее n элементов. Выберем из этого множества k элементов без возвращения, но упорядочивая их по мере их выбора в последовательную цепочку. Такие цепочки называются размещениями.
Размещениями из n элементов по k элементов называются такие комбинации, из которых каждое содержит k элементов, взятых из числа данных n элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одного), либо порядком их расположения.
Поясним это на следующем примере. Пусть имеется три элемента: a, b и c. Тогда из этих трёх элементов можно составить шесть размещений по два элемента: ab, ac, ba, bc, ca, cb. Все приведённые размещения отличаются друг от друга хотя бы одним элементом или порядком их расположения.
Число размещений  (читается: число размещений из n элементов по k элементов) можно найти из принципа умножения. Первый элемент размещения можно выбрать n способами. Как только такой выбор будет сделан, останется (n–1) возможностей, чтобы выбрать второй элемент; после этого останется (n–2) возможностей для выбора третьего элемента и т.д.; для выбора k-го элемента будет (n–k+1) возможностей. По принципу умножения находим
(читается: число размещений из n элементов по k элементов) можно найти из принципа умножения. Первый элемент размещения можно выбрать n способами. Как только такой выбор будет сделан, останется (n–1) возможностей, чтобы выбрать второй элемент; после этого останется (n–2) возможностей для выбора третьего элемента и т.д.; для выбора k-го элемента будет (n–k+1) возможностей. По принципу умножения находим
 . (4.1)
. (4.1)
Легко понять, что  .
.
Пример 4.1. В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить 4 различных фотографии. Сколькими способами это можно сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение. Для размещения фотографий следует отобрать 4 различных страницы из 12 имеющихся. Затем нужно отобранные страницы упорядочить, т.е. определить, на какую страницу поместить первую фотографию, на какую – вторую и т.д. Полученная упорядоченная совокупность страниц является, согласно определению, размещением из 12 элементов по 4, а число таких размещений является искомым результатом:
 .
.
Пример 4.2. Сколькими способами можно составить трехцветный полосатый флаг, если имеются ткани пяти различных цветов? Решите эту же задачу при условии, что одна полоса должна быть красной.
Решение. Поскольку в данной задаче важен порядок следования полос и все цвета во флаге должны быть разными, то исходная задача сводится к подсчету числа размещений из 5 по 3:
 способов.
способов.
При условии, что одна полоса должна быть красной, получаем, что для выбора места для красной полосы существует 3 способа, а для оставшихся двух полос останется 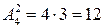 способов. Таким образом, трехцветный полосатый флаг из имеющихся 5 цветов при условии, что один цвет должен быть красным можно составить
способов. Таким образом, трехцветный полосатый флаг из имеющихся 5 цветов при условии, что один цвет должен быть красным можно составить
 способами.
способами.
Пример 4.3. Сколькими способами 10 человек можно поставить парами в ряд?
Решение. Первую пару можно выбрать  способами, вторую –
способами, вторую –  способами, и т.д. В результате получаем
способами, и т.д. В результате получаем
 способами.
способами.
Упражнения
4.1. Научное общество состоит из 25 человек. Надо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами может быть сделан этот выбор, если каждый член общества может занимать лишь один пост?
Ответ: В этом случае надо число размещений из 25 элементов по 4. Здесь играет роль и то, кто будет выбран в руководство общества, и то, какие посты займут выбранные. Поэтому ответ дается формулой  .
.
4.2. В цехе работают 8 токарей. Сколькими способами можно поручить трем из них изготовление различных видов деталей (по одному виду на каждого).
Ответ:  .
.
4.3. Из 10 книг выбирают 4 для рассылки по разным адресам. Сколькими способами это можно сделать?
Ответ:  .
.
4.4. Сколькими способами можно опустить 5 писем в 11 почтовых ящиков, если в каждый ящик опускают не более одного письма?
Ответ: 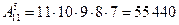 .
.
4.5. Студенту необходимо сдать 5 экзаменов в течение 12 дней. Сколькими способами можно составить расписание экзаменов, если в течение дня он может сдать не более одного экзамена?
Ответ:  .
.
4.6. Сколькими способами можно преподнести 4 различных подарка 6 ученикам таким образом, чтобы каждый ученик получил не более одного подарка?
Ответ:  .
.
4.7. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, …, 9, если каждая цифра в обозначении числа встречается не более одного раза? (Учесть, что число не может начинаться с нуля.)
Ответ:  .
.
ПЕРЕСТАНОВКИ
Рассмотрим частный случай, когда k=n. Соответствующее этому случаю размещение называется перестановкой.
Перестановками из n элементов называются такие комбинации, каждая из которых содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.
Поясним это на следующем примере. Из этих трёх элементов: a, b и c. можно составить шесть перестановок: abc, acb, bac, bca, cab, cba. Все приведённые перестановки отличаются друг от друга только порядком их расположения.
Число перестановок n различных элементов обозначают символом Pn и равно

Пример 5.1. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?
Решение. Будем считать выделенные книги за одну книгу. Тогда уже для шести книг существует P6=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой P4=4!=24 способами. По принципу умножения имеем
P6P4 = 720×24 = 17280.
Пример 5.2. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра в изображении числа встречается один раз?
Решение. Рассматриваемое число может быть представлено как некоторая перестановка из цифр 0, 1, 2, 3, в которой первая цифра отлична от нуля. Так как число перестановок из четырех цифр равно P4=4! и из них 3! перестановок начинаются с нуля, то искомое количество равно
4! – 3! = 3×3! = 3×1×2×3 = 18.
Пример 5.3. Сколькими способами можно посадить за круглый стол n мужчин и n женщин так, чтобы никакие два лица одного пола не сидели рядом?
Решение. Естественно предположить, что как мужчины, так и женщины различимы. Предположим также, что места за столом также различимы. Пронумеруем их. Если женщины займут чётные места n! способами, то мужчины будут занимать нечётные места тоже n! способами и наоборот. По правилу умножения получаем  .
.
Если места за столом неразличимы, то стол можно поворачивать на одно место, то при этом расположение сидящих не изменится (такая ситуация имеет место, например, на карусели). Поскольку имеется n способов расположения стола относительно сидящих, то предыдущий результат нужно разделить на n.

Вопрос. Сколькими способами можно посадить за круглый стол n супружеских пар, если супруги должны сидеть рядом?
Упражнения
5.1. Сколькими способами можно обить 6 стульев тканью, если имеются ткани 6 различных цветов и все стулья должны быть разного цвета.
Ответ:  .
.
5.2. Дачник выделил на своём участке семь грядок для выращивания овощей, т.к. хочет иметь свои помидоры, огурцы, перец, лук, чеснок, салат и кабачки. Каждый вид должен иметь отдельную грядку. Сколькими способами он может расположить грядки для посадки?
Ответ:  .
.
5.3. Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале?
Ответ:  .
.
5.4. В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?
Ответ: 
5.5. Сколькими способами можно упорядочить множество {1,2,3,…,2n} так, чтобы каждое чётное число стояло на чётном месте?
Ответ:  .
.
5.6. Четыре мальчика и четыре девочки рассаживаются в ряд на восемь подряд расположенных мест, причем мальчики садятся на четные места, а девочки – на нечетные. Сколькими способами они могут это сделать?
Ответ:  .
.
5.7. Сколькими способами можно посадить за круглый стол трех мужчин и трех женщин так, чтобы никакие два лица одного пола не сидели рядом?
Ответ:  .
.
5.8. На собрании должны выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов, если Б не должен выступать до того, как выступил А? Решите эту же задачу, если Б должен выступить сразу после А.
Ответ: 5!/2=60; 4!=24.
СВОЙСТВА РАЗМЕЩЕНИЙ И ПЕРЕСТАНОВОК
Рассмотрим задачи, связанные со свойствами размещений и перестановок.
Пример 6.1. Вычислить
 .
.
Решение. Поскольку
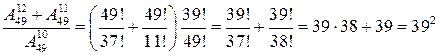
и
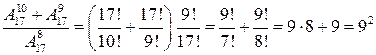 ,
,
то
 .
.
Пример 6.2. Упростить выражение
 (n ³ 6).
(n ³ 6).
Решение. Поскольку
 ,
,  ,
,
 ,
,
 ,
,
то
 .
.
Пример 6.3. Решить неравенство
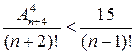 .
.
Решение. Из условия задачи следует, что n³1 и nÎ¥. Поскольку
 ,
,  ,
,
то

и данное в условии неравенство равносильно неравенству
 .
.
Пусть n³2, тогда  , т.е. 20<15. Противоречие, следовательно, n=1 не является решением данного неравенства.
, т.е. 20<15. Противоречие, следовательно, n=1 не является решением данного неравенства.
Пусть n=1, тогда исходное неравенство равносильно следующему
 ,
,
Отсюда следует, что первоначальное неравенство имеет три решения:
n1=3, n2=4 и n3=5.
Упражнения
6.1. Вычислить: а)  , б)
, б)  .
.
Ответ: а) 46, б) 80.
6.2. Упростить:  .
.
Ответ:  .
.
6.3. Решить неравенство  .
.
Ответ:  .
.
6.4. Найти все натуральные n, удовлетворяющие условию:
а)  , б)
, б)  , в)
, в)  .
.
Ответ: а) 4, б) 4, в) 10.
6.5. Доказать, что  .
.
СОЧЕТАНИЯ
Пусть опыт состоит в выборе k элементов без возвращения и без упорядочения из некоторого множества, содержащего n элементов. Исходами такого опыта будут подмножества, содержащие k элементов и отличающиеся друг от друга только составом. Получаемые при этом комбинации элементов называются сочетаниями.
Сочетаниями из n элементов по k элементов называются такие комбинации, из которых каждое содержит k элементов, взятых из числа данных n элементов, и которые отличаются друг от друга хотя бы одним элементом.
Поясним это на следующем примере. Пусть имеется три элемента: a, b и c. Из этих трёх элементов, в отличие от размещений, можно составить три сочетания по два элемента: ab, ac, bc, ca. Все приведённые сочетания отличаются друг от друга хотя бы одним элементом.
Для иллюстрации различий между сочетаниями и размещениями рассмотрим следующий пример. Пусть выбирается делегация в составе 3 человек из 30 учеников. Здесь, очевидно, не надо учитывать порядок выбранных делегатов, т.к. все члены делегации равноправны. Поэтому каждый такой выбор будет сочетанием из 30 по 3. Однако, выбирая старосту, профорга и физорга из тех же учеников, порядок уже приходится учитывать. В этом случае каждый конкретный результат будет уже размещением из 30 по 3.
Найдем число возможных сочетаний  . Чтобы получить размещение из n элементов по k, а их число равно
. Чтобы получить размещение из n элементов по k, а их число равно  , надо выбрать k элементов из множества, содержащего n элементов, что можно сделать
, надо выбрать k элементов из множества, содержащего n элементов, что можно сделать  способами, и организовать из них упорядоченное подмножество. Последнюю операцию можно выполнить Pn способами. Таким образом, чтобы получить
способами, и организовать из них упорядоченное подмножество. Последнюю операцию можно выполнить Pn способами. Таким образом, чтобы получить  размещений, надо выполнить две операции, которые можно осуществить
размещений, надо выполнить две операции, которые можно осуществить  и Рn способами, соответственно. Поэтому, согласно принципу умножения, можно записать
и Рn способами, соответственно. Поэтому, согласно принципу умножения, можно записать
 . (7.1)
. (7.1)
Отсюда получаем, что число сочетаний будет равно
 . (7.2)
. (7.2)
Заметим, что  ,
,  .
.
Пример 7.1. Сколькими способами можно составить комиссию в составе из трех человек из имеющихся 9 человек, 4 женщин и 5 мужчин, если: а) не важен пол членов комиссии; б) комиссия должна состоять из двух женщин и одного мужчины.
Решение. а) Из смысла задачи следует, что порядок выбора членов комиссии не играет роли. Здесь важен только состав. Тогда выбрать комиссию из трех человек из 9 имеющихся можно

способами.
б) Двух женщин из 4 имеющихся можно выбрать  способами, а одного мужчину из 5 можно
способами, а одного мужчину из 5 можно  способами. Тогда общее количество способов выбора комиссии, в соответствии с принципом умножения, можно
способами. Тогда общее количество способов выбора комиссии, в соответствии с принципом умножения, можно

способами.
Пример 7.2. Сколькими различных правильных дробей можно составить из чисел 1, 2, 3, 5, 7, 11, 13, берущихся попарно?
Решение. Различных пар из данных чисел, в которых первый элемент меньше второго, будет, очевидно, столько, сколько можно составить сочетаний из 7 по 2:
 .
.
Пример 7.3. Сколько существует делителей числа 210?
Решение. Разложим данное число на простые множители:  . Число делителей, составленных из произведения двух простых множителей, равно
. Число делителей, составленных из произведения двух простых множителей, равно  (а именно числа 6, 10, 14, 15, 21,35); число делителей, составленных из произведения трёх простых множителей, равно
(а именно числа 6, 10, 14, 15, 21,35); число делителей, составленных из произведения трёх простых множителей, равно  (а именно числа 30, 42, 70, 105); число простых делителей равно четырём (а именно 2, 3, 5, 7). Кроме того, делителями являются число 1 и число 210. Итак, согласно принципу сложения, число всех делителей равно
(а именно числа 30, 42, 70, 105); число простых делителей равно четырём (а именно 2, 3, 5, 7). Кроме того, делителями являются число 1 и число 210. Итак, согласно принципу сложения, число всех делителей равно
 .
.
Эту задачу можно решить и по-другому. Натуральное число N можно разложить на простые множители следующим образом:
 ,
,
1, 2, …, n – некоторые натуральные числа. Число pi может войти в данный делитель с показателем 0, 1, …, n – всего n+1 способами. Из принципа умножения получаем, что число делителей числа N равно
 . (7.3)
. (7.3)
Для числа 210 число делителей по формуле (7.3) будет равно (1=2=3=4=1)
2×2×2×2=16.
Упражнения
7.1. Сколькими способами можно выбрать 5 делегатов из состава конференции, на которой присутствуют 15 человек?
Ответ:  .
.
7.2. У одного студента есть 11 книг по математике, а другого – 15 книг. Сколькими способами они могут выбрать по 3 книги для обмена?
Ответ:  .
.
7.3. Сколько прямых провести через 8 точек, никакие три из которых не лежат на одной прямой?
Ответ:  .
.
7.4. Найти число диагоналей n-угольника.
Ответ:  .
.
7.5. Компания из 15 человек разделяется на две группы, одна из которых состоит из 6 человек, а другая – из 9 человек. Сколькими способами это можно сделать?
Ответ:  .
.
7.6. В пространстве даны 7 точек, никакие четыре из которых не лежат в одной плоскости. Сколько различных плоскостей можно провести через эти точки?
Ответ:  .
.
7.7. В урне 6 белых и 8 черных шаров. Из нее одновременно вынимают три шара одного цвета. Сколькими способами это можно сделать?
Ответ:  .
.
7.8. В колоде десять карт, из которых три – тузы. Наудачу последовательно вынимается, запоминаются и возвращаются в колоду четыре карты. После каждого возвращения карты колода перемешиваются. Сколько возможно случаев, когда среди вытянутых карт окажется хотя бы один туз?
Ответ:  .
.
7.9. В лаборатории работают 8 физиков и 10 химиков. Надо создать рабочие группы по трем темам. В первую группу должны войти 4 физика, во вторую – 5 химиков, а третья должна состоять из 3 человек, которые могут быть как физиками, так и химиками. Сколькими способами можно создать такие группы?
Ответ: 
комбинаторика вероятность бином ньютон
СВОЙСТВА СОЧЕТАНИЙ
Отметим некоторые свойства сочетаний:
1.  (свойство симметрии).
(свойство симметрии).
Например, 
2.  (свойство Паскаля).
(свойство Паскаля).
Данное равенство является рекуррентным соотношением для числа сочетаний. С помощью этого равенства можно составить таблицу для нахождения числа сочетаний. Расположим сочетания в виде треугольной таблицы

Полученную треугольную таблицу принято называть треугольником Паскаля.
3.  .
.
Пример 8.1. Решить уравнение
 .
.
Решение. Поскольку  , то получим квадратное уравнение
, то получим квадратное уравнение
 .
.
Учитывая, что  , получаем решение
, получаем решение
 .
.
Пример 8.2. Решить неравенство
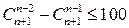 .
.
Решение. Из условия задачи следует, что n³2 и nÎ¥. Поскольку
 ,
,  ,
,
то
 .
.
Таким образом, исходное неравенство равносильно неравенству
 .
.
Поскольку при n=10 получаем  , а при n=9 получаем
, а при n=9 получаем  . Учитывая, что n³2 получаем
. Учитывая, что n³2 получаем
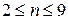 .
.
Пример 8.3. Сколько различных звукосочетаний можно взять на десяти выбранных клавишах рояля, если каждое звукосочетание может содержать от трех до десяти звуков?
Решение. Для звукосочетания клавиши нажимаются одновременно, поэтому для k звуков имеем  звукосочетаний. Таким образом, искомое количество есть
звукосочетаний. Таким образом, искомое количество есть
 .
.
Учитывая свойство 3, т.е., что
 ,
,
получим
 .
.
Упражнения
8.1. Вычислить: а)  , б)
, б)  .
.
Ответ: а) 81, б) 1.
8.2. Упростить:  .
.
Ответ: 2.
8.3. Найти все натуральные n, удовлетворяющие условию:
а)  , б)
, б)  .
.
Ответ: а) 3, б) 14.
8.4. Решить неравенство: а) 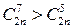 , б)
, б)  .
.
Ответ: а)  , б)
, б)  ,
,
8.5. Доказать, что  .
.
8.6. Имеется 12 различных цветов. Сколькими способами можно составить букет из данных цветов, если в букет должно входить не менее 3 цветов?
Ответ:  .
.