 |
|
ВЕРОЯТНОСТЬ ПОЯВЛЕНИЯ ХОТЯ БЫ ОДНОГО СОБЫТИЯ
В жизни, производстве часто возникают такие ситуации, когда нужно вычислить вероятность появления хотя бы одного события из некоторого набора возможных событий. Например, если по цели был сделан залп из нескольких орудий, то интерес представляет вероятность того, что цель будет поражена, т.е. что будет хотя бы одно попадание.
Два несовместных события A и  называются противоположными, если при эксперименте одно из них обязательно произойдет. Иначе, для противоположных событий справедливы равенства:
называются противоположными, если при эксперименте одно из них обязательно произойдет. Иначе, для противоположных событий справедливы равенства:
 ,
,  .
.
Вероятности противоположных событий связаны соотношением
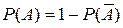 (18.1)
(18.1)
Вероятность появления хотя бы одного из событий A1, A2,…, An равна разности между единицей и вероятности совместного появления противоположных событий:
 . (18.2)
. (18.2)
Если события A1, A2,…, An независимы и их вероятности одинаковы, т.е. 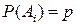 и
и  , то
, то
 . (18.3)
. (18.3)
Пример 18.1. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1=0,8, p2=0,7, p3=0,9. Найти вероятность хотя бы одного попадания при одном залпе из всех орудий.
Решение. Поскольку вероятности попаданий независимы и q1=1–p1=0,2, q2=1–p2=0,3, q3=1–p3=0,1, то искомая вероятность равна
P(A) = 1–q1q2q3 = 1–0,006 = 0,994.
Пример 18.2. Уличный торговец предлагает прохожим иллюстрированную книгу. Из предыдущего опыта ему известно, что в среднем один из 65 прохожих, которым он предлагает книгу, покупают ее. В течение некоторого промежутка времени он предложил книгу 20 прохожим. Чему равна вероятность того, что он продаст им хотя бы одну книгу?
Решение. Пусть Ai – событие того, что i-й прохожий купит книгу. Вероятность этого события  , а противоположного события
, а противоположного события  . Тогда вероятность того, что хотя бы один из 20 прохожих купят книгу, будет равна
. Тогда вероятность того, что хотя бы один из 20 прохожих купят книгу, будет равна
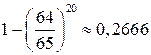 .
.
Пример 18.3. Вероятность того, что при одном выстреле стрелок попадет в цель, равна p=0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?
Решение. Вероятность попадания хотя бы один раз при n выстрелах равна:
P(A) = 1 – qn,
где q=1–p. Поскольку P(A)³0,9, то
1 – qn ³ 0,9 Þ qn £ 0,1 Þ n lg q £ lg0,1 Þ
 .
.
Таким образом, чтобы хотя бы один раз попасть в цель с вероятностью не менее 0,9, стрелок должен произвести не менее 5 выстрелов.
Упражнения
18.1. Отдел маркетинга фирмы проводит опрос для выяснения мнений потребителей по определенному типу продуктов. Известно, что в местности, где проводятся исследования, 10% населения являются потребителями интересующего фирму продукта и могут дать ему квалифицированную оценку. Компания случайным образом отбирает 10 человек из всего населения. Чему равна вероятность того, что, по крайней мере, один человек из них может квалифицированно оценить продукт?
Ответ. 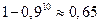 .
.
18.2. Пакеты акций, имеющихся на рынке ценных бумаг, могут дать доход владельцу с вероятностью 0,5 (для каждого пакета). Сколько пакетов акций различных фирм нужно приобрести, чтобы с вероятностью, не меньшей 0,96875, можно было ожидать доход хотя бы по одному пакету акций?
Ответ. Из уравнения 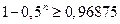 получаем, что не менее 5 пакетов.
получаем, что не менее 5 пакетов.
18.3. Для рыночного исследования необходимо проведение интервью с людьми, которые добираются на работу общественным транспортом. В районе, где проводится исследование, 75% людей добираются на работу общественным транспортом. Если три человека согласны дать интервью, то чему равна вероятность того, что, по крайней мере, один из них добирается на работу общественным транспортом?
Ответ.  .
.
18.4. Модельер, разрабатывающий новую коллекцию одежды к весеннему сезону, создает модели в зеленой, черной и красной цветовой гамме. Вероятность того, что зеленый цвет будет в моде весной, модельер оценивает в 0,3, что черный – в 0,2, а вероятность того, что будет моден красный цвет – в 0,15. Предполагая, что цвета выбираются независимо друг от друга, оцените вероятность того, что цветовое решение коллекции будет удачным хотя бы по одному из выбранных цветов?
Ответ. P=1 – 0,7×0,8×0,85 = 0,524
18.5. Предположим, что для одной торпеды попасть в цель равна 0,7. Какова вероятность того, что три торпеды потопят корабль, если для потопления корабля достаточно одного попадания в цель?
Ответ. 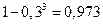 .
.
ЗАДАЧИ
1. Вычислить:
а) 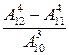 , ,
| б)  , ,
| в)  , ,
|
г)  , ,
| д)  , ,
| е) 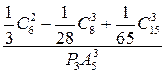 . .
|
Ответ: а) 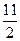 ; б) 4; в) 1; г) 42; д) 4; е)
; б) 4; в) 1; г) 42; д) 4; е)  .
.
2. Упростить:
а) 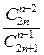 , ,
| б)  , ,
| в)  , ,
|
г) 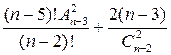 , ,
| д) 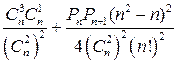 , ,
| е) 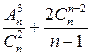 . .
|
Ответ: а)  ; б)
; б) 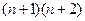 ; в)
; в) 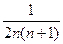 ; г)
; г)  ; д)
; д) 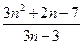 ; е)
; е)  .
.
3. Решить уравнения (nÎ¥):
а) 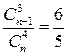 , ,
| б)  , ,
| в) 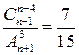 , ,
|
г) 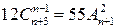 , ,
| д) 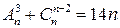 , ,
| е) 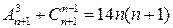 . .
|
Ответ: а) 8; б) 4; в) 10; г) 8; д) 5; е) 4.
4. Найти все n΢, удовлетворяющие условию:
а) 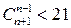 , ,
| б)  , ,
| в)  , ,
|
г) 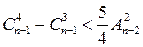 , ,
| д) 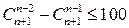 , ,
| е)  . .
|
Ответ: а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 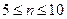 ; д)
; д) 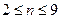 ; е)
; е) 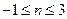 .
.
5. Доказать справедливость равенств:
а)  , ,
| б)  , ,
| в)  , ,
|
г)  , ,
| д) 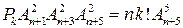 , ,
| е)  . .
|
6. Разложить по формуле бинома Ньютона и упростить:
а)  , ,
| б)  , ,
| в) 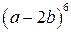 , ,
| г)  . .
|
Ответ: а)  ;
;
б)  ; в)
; в)  ;
;
г) 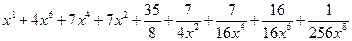 .
.
7. Найти средние члены разложения:
а)  ,
,
б)  .
.
Ответ: а)  и
и 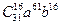 ; б)
; б) 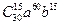 .
.
8. Решите уравнения:
а)  б)
б) 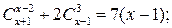 в)
в) 
Ответ: а) 4; б) 5; в) 9.
9. У одного человека есть 7 книг по математике, а у другого – 9 книг. а) Сколькими способами они могут обменять книгу одного на книгу другого? б) То же самое, но меняются две книги одного на две книги другого.
Ответ: а)  ; б)
; б)  .
.
10. Несколько человек садятся за круглый стол. Будем считать, что два способа рассадки совпадают, если каждый человек имеет одних и тех же соседей в обоих случаях. а) Сколькими различными способами можно посадить четырех человек? б) семь человек? в) Во скольких случаях два данных человека из семи оказываются соседями? г) Во скольких случаях данный человек (из семи) имеет двух данных соседей?
Решение: а) Отношение соседства сохраняется при циклических перестановках и при симметричном отражении. В случае четырех человек мы имеем 2×4=8 преобразований, сохраняющих отношение соседства. Т.к. общее число перестановок 4 человек равно 4!=24, то имеем 24/8=3 различных способа рассадки.
б) Если за столом сидят 7 человек, то имеем 7!/14=360 способов, вообще, а в случае n человек (n–1)!/2 способов.
в) Число способов, при которых 2 данных человека сидят рядом, вдвое больше числа способов посадить 6 человек (в силу возможности поменять этих людей местами). Значит оно равно 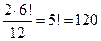 .
.
г) Находится аналогичным образом:  .
.
11. Сколькими способами можно посадить за круглый стол 5 мужчин и 5 женщин так, чтобы никакие два лица одного пола не сидели рядом? Если они садятся не за круглый стол, а за карусель и способы, переходящие друг в друга при вращении карусели, считаются совпадающими.
Ответ:  ,
, 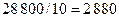 .
.
12. Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется хотя бы один туз? Во скольких случаях ровно один туз? Во скольких случаях не менее двух тузов? Ровно два туза?
Ответ: 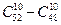 ,
,  ,
,  ,
,  .
.
13. В купе ж/д вагона имеется два противоположных дивана по 5 мест в каждом. Из 10 пассажиров четверо желают сидеть лицом к паровозу, а трое – спиной, остальным безразлично как сидеть. Сколькими способами могут разместиться пассажиры?
Решение: Сначала выберем, кто из трех пассажиров, кому безразлично как сидеть, сядет лицом к паровозу. Этот выбор можно сделать 3 способами. На каждом диване можно пересаживать пассажиров 5! Способами. Всего получаем 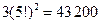 способов.
способов.
14. У мамы 2 одинаковых яблока и 3 одинаковых груши. Каждый день в течение пяти дней подряд она выдает по одному фрукту. а) Сколькими способами это можно сделать? б) Если яблок m, а груш n. в) 2 яблок,3 груши, 4 апельсина.
Ответ: а)  ; б)
; б)  , в)
, в)  .
.
15. У отца есть 5 различных апельсинов, которые он выдает своим 8 сыновьям так, что каждый получает либо один апельсин, либо ничего. Сколькими способами можно это сделать? Решите эту задачу при условии, что число апельсинов, получаемых каждым сыном, неограниченно.
Ответ:  ;
; 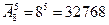 .
.
16. Из группы, состоящей из 7 мужчин и 4 женщин. Надо выбрать 6 человек так, чтобы среди них было не меньше 2 женщин. Сколькими способами можно это сделать?
Ответ:  .
.
17. Найти сумму всех трёхзначных чисел, которые можно написать с помощью цифр 1, 2, 3, 4. А если никакая цифра не должна появляться дважды в записи каждого числа?
Решение: Всего таких чисел  , в них
, в них  цифр, каждая из 4 цифр употребляется
цифр, каждая из 4 цифр употребляется  раза – в каждом из трёх разрядов
раза – в каждом из трёх разрядов 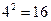 раз, поэтому сумма цифр первого разряда даст 16 (1+2+3+4)=160, второго –1600 и третьего –16000. Сумма равна 17760.
раз, поэтому сумма цифр первого разряда даст 16 (1+2+3+4)=160, второго –1600 и третьего –16000. Сумма равна 17760.
Если цифры не повторяются, то таких чисел  , в них 72 цифры, каждая из 4 цифр употребляется в каждом из 3 разрядов 6 раз, поэтому сумма 6(1+2+3+4)(1+10+100)=6660.
, в них 72 цифры, каждая из 4 цифр употребляется в каждом из 3 разрядов 6 раз, поэтому сумма 6(1+2+3+4)(1+10+100)=6660.
18. Сколько различных четырехзначных чисел, делящихся на 4, можно составить из цифр 1,2, 3, 4, 5, если каждая цифра может встречаться в записи числа несколько раз? А если каждая цифра встречается лишь один раз?
Решение: Число должно оканчиваться: 12, 24, 32, 44, 52; первые же две цифры могут быть произвольными. Всего получаем 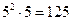 чисел. Во втором случае число должно оканчиваться на одну из четырёх комбинаций: 12, 32, 52, 24; первые же две цифры могут быть выбраны из оставшихся трёх
чисел. Во втором случае число должно оканчиваться на одну из четырёх комбинаций: 12, 32, 52, 24; первые же две цифры могут быть выбраны из оставшихся трёх  способами. Всего получаем 24 числа.
способами. Всего получаем 24 числа.
19. Компания из 7 юношей и 10 девушек танцует парами. а) Если в каком-либо танце участвуют все юноши, то сколько имеется вариантов участия девушек в этом танце? Сколько имеется вариантов, если учитывать лишь то, какие девушки остались неприглашенными? б) Решить те же вопросы, если относительно двух девушек можно с уверенностью утверждать, что они будут приглашены на танец.
Ответ: а)  ,
, 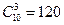 . б)
. б) 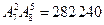 ,
,  .
.
20. Рота состоит из 3 офицеров, 6 сержантов, 60 рядовых. Сколькими способами можно выделить из них отряд, состоящий из одного офицера, двух сержантов и 20 рядовых? Решить эту задачу, при условии, что в отряд должны войти командир роты и старший из сержантов.
Ответ: 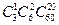 ;
; 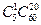 .
.
21. На школьном вечере присутствуют 12 девушек и 15 юношей. Сколькими способами можно выбрать из них 4 пары для танца?
Ответ: 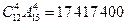 .
.
22. Сколькими способами можно расставить 20 книг в книжном шкафу с 5 полками, если каждая полка может вместить все 20 книг?
Ответ: Добавим к 20 книгам 4 одинаковых разделительных предмета и рассмотрим все перестановки полученных объектов. Их число равно 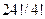 .
.
23. Сколькими способами можно надеть 5 различных колец на пальцы одной руки, исключая большой палец?
Ответ: Точно так же как предыдущей задаче  .
.
24. 30 человек голосуют по 5 предложениям. Сколькими способами могут распределиться голоса, если каждый голосует за одно предложение и учитывается лишь число голосов, полученных за каждое предложение?
Решение: Так как учитывается лишь число голосов, поданных за каждое предложение, то надо распределить 30 одинаковых «предметов» по 5 «ящикам». Для этого добавим 4 одинаковых разделительных предмета и рассмотрим все перестановки полученных объектов. Их число равно 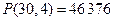 . Каждой перестановке соответствует своё распределение голосов.
. Каждой перестановке соответствует своё распределение голосов.
25. Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневый переплеты. Сколькими способами он может это сделать, если в каждый цвет должны быть переплетены хотя бы одна книга?
Решение: 12 книг можно переплести в переплеты трёх цветов  способами. Из них в
способами. Из них в  случаях книги будут переплетены в не более чем два цвета, а в трех случаях – в один цвет. По формуле включений и исключений в
случаях книги будут переплетены в не более чем два цвета, а в трех случаях – в один цвет. По формуле включений и исключений в 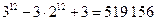 случаях книги будут переплетены в переплеты всех цветов.
случаях книги будут переплетены в переплеты всех цветов.
26. Сколькими способами можно выбрать 12 человек из 17, если данные двое человек из этих 17 не могут быть выбраны вместе?
Ответ: 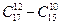 .
.
27. Хор состоит из 10 участников. Сколькими способами можно в течение трех дней выбирать по 6 участников, так, чтобы каждый день были различные составы хора?
Ответ:  .
.
28. Человек имеет 6 друзей и в течение 20 дней приглашает к себе 3 из них так, что компания ни разу не повторяется. Сколькими способами можно это сделать?
Ответ: Так как 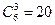 , то каждый способ выбора компании будет использован ровно один раз. Число перестановок этих способов равно 20!
, то каждый способ выбора компании будет использован ровно один раз. Число перестановок этих способов равно 20!
29. Для премии по математической олимпиаде выбраны 3 экземпляра одной книги, 2 экземпляра другой и 1 экземпляр третьей книги. Сколькими способами могут быть вручены премии, если в олимпиаде участвовало 20 человек и никому не дают две книги сразу? Если никому не дают двух экземпляров одной и той же книги, но могут быть вручены две или три различные книги?
Решение: Сначала выберем призеров, а потом распределим между ними книги. В результате по принципу умножения получаем 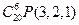 способов. Во втором случае сначала выберем, кто получил первую книгу, потом, кто получил вторую, и, наконец, кому достанется третья книга. Всего получаем
способов. Во втором случае сначала выберем, кто получил первую книгу, потом, кто получил вторую, и, наконец, кому достанется третья книга. Всего получаем 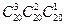 способов распределения премий.
способов распределения премий.
30. Сколькими способами можно выбрать из 16 лошадей шестерку для запряжки так, чтобы вошли 3 лошади из шестерки ABCA'B'C', но ни одна из пар AA', BB', CC'?
Решение: Выберем по одной лошади из каждой пары AA', BB', CC' (8 способов выбора), трех лошадей из остальных 10 ( 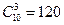 способов) и выберем порядок запрягания лошадей (6! способов). Всего
способов) и выберем порядок запрягания лошадей (6! способов). Всего  способов.
способов.
31. Сколькими способами можно переставить буквы в слове «фатеция» так, чтобы не менялся порядок гласных букв?
Решение: Выпишем сначала гласные в данном порядке. Тогда для буквы «ф» имеем 5 мест. После того как они выписаны, имеем 6 мест для буквы «ц» и, наконец, 7 мест для буквы «м». Всего  способов.
способов.
32. Сколькими способами можно переставить буквы в слове «параллелизм» так, чтобы не менялся порядок гласных букв?
Ответ:  (следует учесть, что буква «л» входит в слово трижды.
(следует учесть, что буква «л» входит в слово трижды.
33. Сколькими способами можно переставить буквы слова «Юпитер» так, чтобы гласные шли в алфавитном порядке?
Ответ: 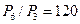 .
.
34. Сколькими способами можно переставить буквы слова «пастух» так, чтобы между двумя гласными были две согласные?
Ответ: Сначала фиксируем порядок гласных (2 способа), затем поставим между этими гласными 2 согласные (  способов). Первую из оставшихся согласных букв можно поставить до или после обеих гласных (два способа), а для второй имеем уже три места. Всего получаем
способов). Первую из оставшихся согласных букв можно поставить до или после обеих гласных (два способа), а для второй имеем уже три места. Всего получаем 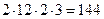 способа.
способа.
35. Сколькими способами можно распределить 3n предметов между тремя людьми так, чтобы каждый получил n предметов?
Ответ: Расставим предметы в некотором порядке и отдадим первому человеку первые n предметов, второму – вторые n предметов и последнему – оставшиеся предметы. Поскольку порядок элементов в группах не играет роли, получаем  .
.
36. Сколькими способами можно разложить 10 книг на 5 бандеролей по 2 книги в каждой (порядок бандеролей не принимается во внимание)?
Ответ: 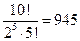 .
.
37. Сколькими способами можно раздать 18 различных предметов 5 участникам так, чтобы четверо из них получили по 4 предмета, а пятый – два предмета. Если трое получают по 4 предмета, а двое – по 3 предмета?
Решение: Располагаем участников раздела в некотором порядке. После этого располагаем всеми способами 18 предметов по порядку и делим на 4 группы по 4 предмета и 1 группу в 2 предмета. Группу в 2 предмета отдаём одному из 5 участников раздела, а остальные группы даём остальным (первую группу – первому, вторую – второму и т.д.) Так как порядок элементов в группах не играет роли, получаем 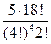 способов раздела. Во втором случае точно так же получаем
способов раздела. Во втором случае точно так же получаем  способов.
способов.
38. Сколькими способами можно раздать 27 книг лицам A, B и C так, чтобы A и B вместе получили вдвое больше книг, чем C?
Решение: Сначала выберем 9 книг для C. Это можно сделать  способами. Оставшиеся 18 книг можно разделить между A и B 218 способами. Всего имеем
способами. Оставшиеся 18 книг можно разделить между A и B 218 способами. Всего имеем  способов раздела.
способов раздела.
39. Сколькими способами можно выбрать из чисел от 1 до 100 три числа так, чтобы их сумма делилась на 3?
Решение: Возможны следующие случаи: на 3 делятся все три слагаемых, одно слагаемое и ни одного из слагаемых. В первом случае слагаемые можно выбрать  способами. Во втором случае одно слагаемое дает в остатке 1, а другое – 2. Так как чисел от 1 до 100, дающих в остатке 1, имеется 34, а чисел, делящихся на 3, а также дающих в остатке 2, имеется по 33, то во втором случае имеем
способами. Во втором случае одно слагаемое дает в остатке 1, а другое – 2. Так как чисел от 1 до 100, дающих в остатке 1, имеется 34, а чисел, делящихся на 3, а также дающих в остатке 2, имеется по 33, то во втором случае имеем  способов. Если все три слагаемых не делятся на 3, то они дают либо остатки 1, 1 и 1, либо 2, 2 и 2. Соответственно получаем
способов. Если все три слагаемых не делятся на 3, то они дают либо остатки 1, 1 и 1, либо 2, 2 и 2. Соответственно получаем 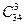 или
или  способов. Всего имеем
способов. Всего имеем  способа.
способа.
40. Сколькими способами можно выбрать из 3n последовательных целых чисел три числа так, чтобы их сумма делилась на 3?
Ответ:  .
.
41. На плоскости проведены 4 прямые линии, из которых никакие две не являются параллельными и никакие 3 не проходят через одну точку. Сколько получится треугольников?
Ответ: 4.
42. На плоскости задано n точек, из которых p лежат на одной прямой, а кроме них никакие 3 точки не лежат на одной прямой. Сколько существует треугольников, вершинами которых являются эти точки?
Решение: Если бы никакие три из n точек лежат на одной прямой, то было бы  треугольников с вершинами в этих точках. Но p точек лежат на одной прямой, и поэтому
треугольников с вершинами в этих точках. Но p точек лежат на одной прямой, и поэтому  треугольников надо отбросить. Остается
треугольников надо отбросить. Остается  треугольников.
треугольников.
43. На прямой взяты p точек, а на другой прямой – ещё q точек. Сколько существует треугольников, вершинами которых являются эти точки?
Ответ: Можно взять две вершины на одной прямой, а третью – на другой. Поэтому получаем 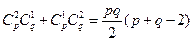 треугольников.
треугольников.
44. Каждая сторона квадрата разбита на n частей. Сколько можно построить треугольников, вершинами которых являются точки деления?
Решение: Треугольники могут быть двух видов: либо все три вершины лежат на разных сторонах квадрата, либо две вершины лежат на одной стороне квадрата, а третья – на какой-либо другой. В первом случае надо выбрать три стороны квадрата из четырех ( 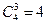 ), а потом на каждой из трех сторон по одной точке из n–1. Всего имеем
), а потом на каждой из трех сторон по одной точке из n–1. Всего имеем  способов выбора. Во втором случае надо выбрать сторону, где лежат две вершины (4 способа выбора) и две точки из n–1 (
способов выбора. Во втором случае надо выбрать сторону, где лежат две вершины (4 способа выбора) и две точки из n–1 (  способов), после чего выбрать одну из трёх оставшихся сторон (три способа) и точку на ней (
способов), после чего выбрать одну из трёх оставшихся сторон (три способа) и точку на ней (  способов). Всего во втором случае имеем
способов). Всего во втором случае имеем  способов выбора. Итого получим
способов выбора. Итого получим  способов.
способов.
45. Переплётчик должен переплести 12 различных книг в красный, зеленый и коричневый переплеты. Сколькими способами он может это сделать, если в каждый цвет должна быть переплетена хотя бы одна книга?
Решение: 12 книг можно переплести в переплеты 3 цветов 312 способами. Из них в  случаях книги будут переплетены в не более чем два цвета, а в 3 случаях – в один цвет. По формуле включений и исключений получаем, что
случаях книги будут переплетены в не более чем два цвета, а в 3 случаях – в один цвет. По формуле включений и исключений получаем, что 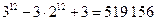 случаях книги будут переплетены всех трех цветов.
случаях книги будут переплетены всех трех цветов.
46. На столе лежат 20 билетов. Какова вероятность того, что 3 наудачу взятых билета имеют номер не больше 5?
Ответ:  .
.
47. В одной урне 3 белых и 5 черных шаров, в другой – 9 белых и 4 черных. Из каждой урны взяли по три шара. Какова вероятность того, что шары будут одного цвета?
Ответ: 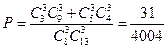 .
.
48. Восемь различных книг случайных образом расставляют на полке. Найти вероятность того, что три определенные книги окажутся рядом?
Ответ:  .
.
49. Зенитная батарея, состоящая из 3 орудий, производит залп по группе, состоящей из 7 самолетам. Каждое из орудий выбирает себе цель наудачу независимо от остальных. Найти вероятность того, что все орудия выстрелят по одному и тому же самолетам.
Ответ:  .
.
50. Для уменьшения общего количества игр 12 команд случайным образом разбиты на две равные подгруппы. Определить вероятность того, что две наиболее сильные команды окажутся в разных подгруппах.
Ответ: 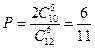 .
.
51. Для уменьшения общего количества игр 2n команд случайным образом разбиты на две равные подгруппы. Определить вероятность того, что две наиболее сильные команды окажутся: а) в разных подгруппах; б) в одной подгруппе.
Ответ: а) 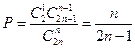 , б)
, б) 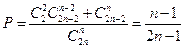 .
.
52. Зенитная батарея, состоящая из k орудий, производит залп по группе, состоящей из l самолетов (k£l). Каждое орудие выбирает себе цель случайно и независимо от других. Найти вероятность того, все k орудий выстрелят по одной и той же цели.
Ответ:  .
.
53. Из множества чисел {1, 2, ... , n} последовательно выбирается два числа. Какова вероятность, что второе число больше первого, если выбор осуществляется: а) без возвращения; б) с возвращением?
Ответ: а) 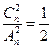 , б)
, б)  .
.
54. Из множества чисел {1, 2, ... , n} последовательно выбирается три числа. Какова вероятность того, что второе число будет заключаться между первым и третьим, если выбор осуществляется: а) без возвращения; б) с возвращением?
Ответ: а)  , б)
, б)  .
.
55. На бочонках лото написаны числа от 1 до N. Из этих N бочонков одновременно случайно выбираются два. Найти вероятность того, что: а) на обоих бочонках написаны числа, меньше чем k (2<k<N); б) на одном из бочонков написано число, большее чем k, а на другом – меньшее чем k.
Ответ: а)  , б)
, б)  .
.
56. N человек случайным образом рассаживаются за круглым столом (N>2). Найти вероятность того, что два фиксированных лица А и В окажутся рядом.
Ответ: 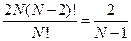 .
.
57. N человек случайным образом рассаживаются за прямоугольным столом вдоль одной из его сторон (N>2). Найти вероятность того, что два определенных лица А и В окажутся рядом.
Ответ:  .
.
58. Урна содержит шары с номерами 1, 2, ... , n. Из нее k (k£n) раз вынимается шар и каждый раз возвращается обратно. Найти вероятность того, что номера вынутых шаров образуют строго возрастающую последовательность.
Ответ:  .
.
59. n различных предметов случайным образом распределяются среди m человек (m<n), причем таким образом, что каждый может получить любое число предметов из числа имеющихся. Какова вероятность того, что определенное лицо не получит ни одного предмета?
Ответ:  .
.
60. В урне имеются n белых, m черных и l красных шаров. Из нее извлекаются с возвращением наудачу по одному шару. Найти вероятность того, что белый шар будет извлечен раньше черного.
Ответ: Так как в условии задачи наличие или отсутствие красных шаров роли не играет, то искомая вероятность равна вероятности вынуть первым белый шар из урны, в которой имеется n белых и m черных шаров, т.е. равна 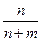 .
.
61. В урне имеются n белых и m черных шаров. Два игрока последовательно достают по одному шару, возвращая каждый раз извлеченный шар. Игра продолжается до тех пор, пока кто-нибудь из них не достанет белый шар. Определить вероятность того, что первым вытащит белый шар игрок, начинающий игру.
Решение: Первый игрок выиграет, если он сразу достанет белый шар, либо если он достанет черный шар (в этом случае вероятность равна 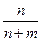 ), второй игрок тоже черный шар, а затем он со второй попытки достанет белый шар (в этом случае вероятность равна
), второй игрок тоже черный шар, а затем он со второй попытки достанет белый шар (в этом случае вероятность равна 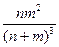 ) и т.д. В результате, используя принцип умножения, получим
) и т.д. В результате, используя принцип умножения, получим

По формуле суммы бесконечно убывающей геометрической прогрессии находим
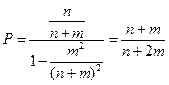 .
.
62. Для проверки собранной схемы последовательно послано три одиночных импульса. Вероятности прохождения каждого из них не зависят от того, прошли остальные или нет, и соответственно равны 0,9, 0,8 и 0,7. Определить вероятность того, что пройдут ровно два посланных импульса.
Ответ. 0,9×0,8×0,3+0,9×0,2×0,7+0,1×0,8×0,7=0,398.
63. Происходит воздушный бой между двумя самолетами: истребителем и бомбардировщиком. Стрельбу начинает истребитель: он дает по бомбардировщику один выстрел и сбивает его с вероятностью p1. Если бомбардировщик этим выстрелом не сбит, он стреляет по истребителю и сбивает его с вероятностью p2. Если истребитель не сбит, он еще раз стреляет по бомбардировщику и сбивает его с вероятностью p3. Найти вероятность того, что будет сбит хотя бы один самолет.
Ответ.  .
.
64. Техническое устройство, состоящее из трех узлов, работало в течение некоторого времени t. За это время первый узел оказывается исправным с вероятностью p1, второй – с вероятностью p2 и третий – с вероятностью p3. Наладчик, вызванный для осмотра устройства, обнаруживает и устраняет неисправность каждого узла, если она имеется, с вероятностью p, а с вероятностью q=1–p объявляет узел исправным. Найти вероятность того, что после осмотра наладчиком хотя бы один узел устройства будет неисправным.
Ответ. 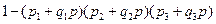 .
.
65. Имеется m радиолокационных станций, каждая из которых за один цикл обзора обнаруживает объект с вероятностью p (независимо от других циклов и от других станций). За определенное время каждая станция успевает сделать n циклов. Найти вероятность того, что: а) объект будет обнаружен хотя бы одной станцией; б) объект будет обнаружен каждой из станций.
Ответ. а)  ; б)
; б)  .
.
66. Ведется стрельба по самолету, уязвимыми агрегатами которого являются два двигателя и кабина пилота. Для того чтобы поразить самолет (вывести его из строя), достаточно поразить оба двигателя или кабину пилота. Найти вероятность того, что самолет будет поражен, если вероятность поражения первого двигателя равна p1, второго – p2 и кабины пилота – p3.
Ответ. 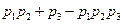 .
.
67. Имеется группа из k космических объектов, каждый из которых независимо от других обнаруживается радиолокационной станцией с вероятностью p. За группой объектов ведут наблюдение независимо друг от друга m радиолокационных станций. Найти вероятность того, что не все объекты, входящие в группу, будут обнаружены.
Ответ. 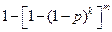 .
.
ВАРИАНТЫ САМОСТОЯТЕЛЬНЫХ РАБОТ
Вариант №1
1.Решить уравнение 
Ответ: n=8.
2.Найти шестой член разложения  .
.
Ответ: 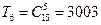 .
.
3.Сколькими способами можно составить колонну из десяти автобусов и трех легковых автомобилей, считая, что все автобусы и все автомобили одинаковых марок?
Ответ:  .
.
4.В шахматном турнире участвуют шесть студентов и три школьника. Сколькими способами могут распределиться места, занятые в турнире школьники, если никакие два участника не набрали одинаковое число очков?
Ответ:  .
.
5.Сколько делителей у числа 105?
Ответ: Разложим число 105 на простые множители  . Тогда
. Тогда  , или по формуле (7.3) получаем
, или по формуле (7.3) получаем 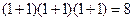 .
.
6.На вечере присутствуют 12 девушек и 15 юношей. Сколькими способами можно выбрать из них 4 пары на танец?
Ответ: 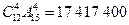 .
.
7.Сколько ожерелий можно составить из 7 бусинок различных размеров (надо использовать все бусинки)?
Ответ: Т.к. ожерелье остается неизменным при циклических перестановках бусинок и при переворачивании, то можно получить 7!/14=360 видов ожерелий.
8.В первой урне находятся 4 белых и 3 черных шара, во второй – 3 белых и 5 черных шаров. Из каждой урны случайным образом вынули по одному шару. Найти вероятность того, что все шары будут белые.
Ответ:  .
.
9.10 вариантов контрольной работы распределены среди 6 студентов. Найти вероятность того, что варианты с номерами 1 и 2 не будут использованы.
Ответ:  .
.
10.Семь различных книг случайных образом расставляют на полке. Найти вероятность того, что книги трехтомника окажутся рядом в возрастающем порядке.
Ответ:  .
.
11.Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочнике соответственно равны 0,6, 0,8 и 0,9. Найти вероятность того, что формула содержится только в двух справочниках.
Ответ. 0,9×0,8×0,3+0,9×0,2×0,7+0,1×0,8×0,7=0,398.
Вариант №2
1. Решить уравнение 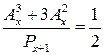 .
.
Ответ: x=4.
2. В разложении 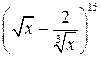 вычислить член, не содержащий x.
вычислить член, не содержащий x.
Ответ: 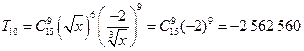 .
.
3. На плоскости проведены n прямых линий, из которых никакие две не являются параллельными и никакие три не пересекаются в одной точке. Сколько точек пересечения имеют эти прямые?
Ответ:  .
.
4. Сколькими способами можно разложить 12 различных марок между тремя мальчиками, если один берёт 6 марок, а остальные – по 3 марки?
Ответ:  .
.
5. Сколько делителей у числа 360?
Ответ: Поскольку  , то в соответствие с формулой (7.3) получаем (3+1)(2+1)(1+1)=24 делителей.
, то в соответствие с формулой (7.3) получаем (3+1)(2+1)(1+1)=24 делителей.
6. В избушке на курьих ножках собрались Баба-Яга, Кощей и Леший. У Бабы-Яги есть 4 чашечки, 5 блюдец и 6 чайных ложечки (все чашки, блюдца и ложечки отличаются друг от друга). Сколькими способами она может накрыть стол для чаепития (каждый получает одну чашку, одно блюдце и одну ложечку)?
Ответ:  .
.
7. Шесть девушек водят хоровод. Сколькими способами они могут организовать хоровод?
Ответ: Т.к. хоровод остается неизменным при циклических перестановках девушек, то можно получить 6!/6=120 способов.
8. В урне находятся 5 белых и 3 черных шаров, из которой случайно по порядку с возвращением вынимаются 4 шара. Какова вероятность того, что первые два шара будут белые, а последние два черные.
Ответ:  .
.
9. Студент пришел на экзамен, зная лишь 24 вопроса из 32 вопросов программы. Экзаменатор задал студенту 3 вопроса. Найти вероятность того, что студент ответ на все вопросы?
Ответ:  .
.
10. Случайным образом выписаны 3 цифры. Найти вероятность того, все цифры различные.
Ответ:  .
.
11. При включении зажигания двигатель начинает работать с вероятностью 0,9. Найти вероятность того, что для запуска двигателя потребуется включить зажигание не более двух раз.
Ответ. 0,9+0,1×0,9=0,99.
Вариант №3
1. Решить уравнение  .
.
Ответ: x=9, x=10.
2. Раскрыть скобки в выражении 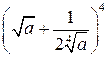 .
.
Ответ: 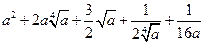 .
.
3. Сколькими способами можно составить шестизначное число, в запись которого входят четыре двойки и две пятёрки?
Ответ:  .
.
4. На пять сотрудников университета выделены три путёвки на один курорт. Сколькими способами их можно распределить, если: а) все путёвки в различные санатории; б) все путёвки в один санаторий.
Ответ: а) 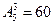 , б)
, б)  .
.
5. Сколькими способами можно выбрать из полной колоды карт, содержащей 52 карты, по одной карте каждой масти? А ели среди вынутых карт нет ни одной пары одинаковых, т.е. двух королей, двух десяток и т.д.?
Ответ: Получаем размещения с повторениями из 13 карт по 4. Всего 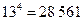 . Если среди карт не должно быть пар, то имеем размещения без повторений; их число
. Если среди карт не должно быть пар, то имеем размещения без повторений; их число  .
.
6. Сколькими способами можно сделать трёхцветный флаг (с тремя горизонтальными полосами), если имеется материя пяти различных цветов, если цвета могут повторяться, но не рядом (полосы должны быть различными)?
Ответ: Осуществляя выбор сверху вниз, получаем 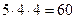 способов.
способов.
7. Из 12 девушек и 10 юношей выбирают команду в составе 5 человек. Сколькими способами можно выбрать эту команду так, чтобы в неё вошло не более 3 юношей?
Ответ: 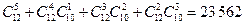 .
.
8. Автобус должен сделать 8 остановок, в котором едут 5 пассажиров. Какова вероятность, что на каждой остановке выйдет не более одного пассажира, если предположить, что каждый пассажир имеет одинаковую вероятность выйти на любой остановке?
Ответ:  .
.
9. На каждой из шести одинаковых карточках напечатана одна из следующих букв: а, т, м, р, с, о. Карточки тщательно перемешаны. Найти вероятность того, что на четырех, вытянутых по одной и расположенных «в одну линию» карточках, можно будет прочесть слово «трос».
Ответ:  .
.
10. Собрание, на котором присутствуют 20 человек, в том числе 8 женщин, выбирают делегацию из 5 человек. Найти вероятность того, что в делегацию войдут 3 женщины, считая, что каждый из присутствующих может быть избран с одинаковой вероятностью.
Ответ:  .
.
11. Вероятность для данного спортсмена улучшить свой предыдущий результат с одной попытки равна 0,6. Определить вероятность того, что на соревнованиях спортсмен улучшит свой результат, если разрешается делать две попытки.
Ответ. 1–0,42=0,84.
Вариант №4
1.Решить уравнение  .
.
Ответ: x=11.
2.Найти член разложения 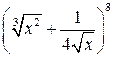 , содержащий x3 .
, содержащий x3 .
Ответ:  .
.
3.Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале?
Ответ:  .
.
4.Из семи гвоздик и пяти тюльпанов надо составить букет, состоящий из трёх гвоздик и двух тюльпанов. Сколькими способами можно это сделать?
Ответ: 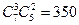 .
.
5.На призывном пункте находится 15 призывников. Сколькими способами можно поставить в колонну по три человека?
Ответ:  .
.
6.Сколькими способами можно выбрать 12 человек из 17, если определенные два человека из этих 17 не могут быть выбраны вместе?
Ответ:  .
.
7.В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?
Ответ:  .
.
8.8 вариантов контрольной работы случайным образом распределены среди 6 студентов. Найти вероятность того, что варианты с номерами 7 и 8 не будут использованы?
Ответ: 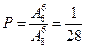 .
.
9.В первой урне находятся 5 оранжевых и 4 фиолетовых шара, во второй – 3 оранжевых и 7 фиолетовых шара. Из каждой урны случайным образом вынули по три шара. Найти вероятность того, что все шары будут одного цвета.
Ответ:  .
.
10.В журнале из 20 страниц на каких-либо трех страницах помещают случайным образом одинаковую рекламу некоторой фирмы. Какова вероятность, что эта реклама будет размещена на страницах, идущих одна за другой?
Решение: В данной задаче порядок размещения рекламы неважен. Следовательно, в данной задаче мы имеем дело с сочетаниями. Общее число размещений рекламы в журнале  . Если реклама будет размещена на страницах, идущих одна за другой, то эти страницы можно считать за одну. Тогда число страниц будет равно 18, следовательно, и число благоприятствующих исходов будет равно m=18. Таким образом,
. Если реклама будет размещена на страницах, идущих одна за другой, то эти страницы можно считать за одну. Тогда число страниц будет равно 18, следовательно, и число благоприятствующих исходов будет равно m=18. Таким образом, 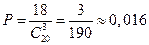 .
.
11.В ОТК поступают 4 детали. Вероятность того, что деталь бракованная равна 0,1. Проверка производится последовательно до обнаружения бракованной детали. Найти вероятность того, что будут проверены все 4 детали.
Ответ. 0,9×0,9×0,9=0,729.
Вариант №5
1.Уравнение  .
.
Ответ: 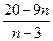 .
.
2.Найти показатель степени бинома  , если его четвёртый член не зависит от a.
, если его четвёртый член не зависит от a.
Ответ: 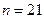 .
.
3. На складе имеются 7 ящиков с различными фруктами и 5 ящика с различными овощами. Сколькими способами можно каждой из трёх овощных палаток выдать по одному ящику с фруктами и овощами?
Ответ:  .
.
4. Сколькими способами 6 одинаковых монет могут распределить между собой Буратино, лиса Алиса и кот Базилио?
Ответ:  .
.
5. В команду должны быть отобраны 4 спортсмена из имеющихся 10. Сколькими способами это можно сделать, если два определенных спортсмена должны войти в команду?
Ответ:  .
.
6. Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях будет ровно один туз?
Ответ:  .
.
7. Пассажирский поезд состоит из четырех багажных вагонов и десяти купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале или конце?
Ответ: 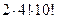
8. Собрание, на котором присутствуют 12 человек, в том числе 7 женщин, выбирают председателя, его первого и второго заместителя. Найти вероятность того, что председатель и его заместители будут женщинами, считая, что каждый из присутствующих может быть избран с одинаковой вероятностью.
Ответ:  .
.
9. В урне находятся 5 зелёных и 3 жёлтых шара. Из урны случайным образом вынули три шара. Найти вероятность того, что все шары будут одного цвета.
Ответ: 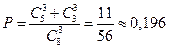 .
.
10. 10 вариантов контрольной работы распределяется среди случайным образом среди 10 студентов, сидящих в один ряд. Найти вероятность того, что варианты с номерами 1 и 2 достанутся рядом сидящим студентам.
Ответ:  .
.
11. Два охотника одновременно и независимо друг от друга стреляют по зайцу. Найти вероятность того, что попадёт только один из охотников, если вероятность попадания для первого охотника равна 0,8, а для второго – 0,7.
Ответ:  .
.
Вариант №6
1.Уравнение 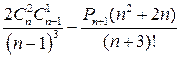 .
.
Ответ:  .
.
2.Найти средний член разложения 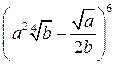 .
.
Ответ:  .
.
3.В пространстве даны 7 точек, причем никакие четыре из них не лежат в одной плоскости. Сколько различных плоскостей можно провести через эти 7 точек?
Ответ:  .
.
4.Эллочка Людоедка решила расставить семь различных книг на полке. Сколькими способами она может это сделать, если две наиболее красивые книги (по её мнению) в красном переплёте должны стоять по краям?
Ответ:  .
.
5.В первенстве края по футболу участвуют 12 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 3 определенные команды?
Ответ:  .
.
6.Сколькими способами декан может раздать 7 поручений 4 студентам?
Ответ: 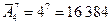 .
.
7.Сколькими способами можно выбрать на шахматной доске белое и черное поля, не лежащее на одной вертикали или горизонтали?
Ответ:  .
.
8.Для проведения тестирования группу студентов, состоящую из 18 человек, случайным образом разбивают на две подгруппы из 12 и 6 человек. Какова вероятность, что две подружки, Оля и Тяня, окажутся в одной подгруппе?
Решение: В данной задаче порядок неважен, т.е. не принимается во внимание порядок отбора студентов в группу. Следовательно, в данной задаче мы имеем дело с сочетаниями. Для того чтобы разбить 18 студентов на две подгруппы достаточно выбрать, например, 12 студентов в одну подгруппу, тогда остальные образуют другую подгруппу. Таким образом, общее число разбиений студентов на две подгруппы будет равно 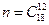 . Для того, чтобы разбить команды на две подгруппы с указанными условиями, можно к Оле и Тане добавить либо 10 студентов из оставшихся 16 (это можно сделать способами
. Для того, чтобы разбить команды на две подгруппы с указанными условиями, можно к Оле и Тане добавить либо 10 студентов из оставшихся 16 (это можно сделать способами  ), либо добавить 4 студентов из 16 (
), либо добавить 4 студентов из 16 (  способов). Оставшиеся студенты будут образовывать другую подгруппу. Таким образом, число благоприятствующих исходов будет равно
способов). Оставшиеся студенты будут образовывать другую подгруппу. Таким образом, число благоприятствующих исходов будет равно  . В результате, получаем
. В результате, получаем  .
.
9.В газете из 16 страниц на каких-либо трех страницах помещают случайным образом разные объявления. Какова вероятность, что эти объявления будут размещены на страницах, идущих одна за другой?
Ответ:  .
.
10.В одной урне 3 зелёных и 4 жёлтых шаров, в другой – 6 зелёных и 2 жёлтых шара. Из каждой урны взяли по два шара. Какова вероятность того, что все шары будут одного цвета?
Ответ: 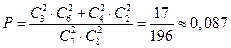 .
.
11.Студент знает 5 вопросов из 12. Какова вероятность того, что он получит зачет, если нужно ответить на все три задаваемых вопроса?
Ответ: 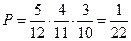 .
.
Вариант №7
1. Решить уравнение  .
.
Ответ: n=5.
2. Найти член разложения 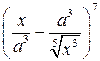 , содержащий x–1.
, содержащий x–1.
Ответ:  .
.
3. Сколько диагоналей можно провести в выпуклом восьмиугольнике?
Ответ: 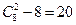 .
.
4. Сколько различных «слов» можно составить, переставляя буквы слова «парабола»?
Ответ:  .
.
5. Труппа состоит из 10 человек. Сколькими способами можно выбирать из неё в течение двух вечеров по 6 человек для участия в спектаклях так, чтобы эти составы не совпадали друг с другом?
Ответ:  .
.
6. Сколькими способами Буратино, лиса Алиса и кот Базилио могут поделить между собой 5 одинаковых золотых монет и 2 разных брильянтовых ожерелья?
Ответ:  .
.
7. Сколькими способами можно разложить 9 книг по 3 бандеролям по 3 книги в каждой (порядок бандеролей не принимать во внимание)?
Ответ: 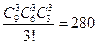 .
.
8. Для проведения тестирования группу студентов, состоящую из 18 человек, случайным образом разбивают на две подгруппы из 12 и 6 человек. Какова вероятность, что две подружки, Оля и Таня, окажутся в разных подгруппах?
Ответ: Решается аналогично задаче 8 предыдущего варианта  .
.
9. Три охотника стреляют по 7 уткам. Каждый из охотников выбирает себе цель наудачу независимо от остальных. Найти вероятность того, что все охотники выстрелят по разным уткам.
Ответ: 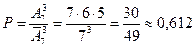 .
.
10. На каждой из шести одинаковых карточках напечатана одна из следующих букв: м, м, а, а. Карточки тщательно перемешаны. Найти вероятность того, что на четырех, вытянутых по одной и расположенных «в одну линию» карточках, можно будет прочесть слово «мама».
Ответ: 
11. Вероятность боя стеклянной тары при погрузке на