 |
|
ФОРМУЛА ВКЛЮЧЕНИЙ И ИСКЛЮЧЕНИЙ
Принцип сложения можно применять в тех случаях, когда все множество перечисляемых комбинаций разбивается на попарно непересекающиеся группы комбинаций. Обобщим принцип сложения на случай, когда могут иметь место случаи непустых пересечений.

Пусть имеется n предметов, которые могут обладать двумя свойствами A и B. При этом каждый предмет может либо не обладать ни одним из этих свойств, либо обладать одним или обоими свойствами. Обозначим через n(A), n(B), n(AB) количество предметов, обладающих свойством A, свойством B, обоими свойствами. Тогда число предметов, обладающих хотя бы одним из указанных свойств, равно
 . (13.1)
. (13.1)
Появление третьего слагаемого связано с тем, что число предметов обладающих обоими свойствами при сложении n(A) и n(B) учитывались дважды (см. рис. 13.1).
Формула (13.1) является частным случаем более общей формулы:
 (13.2)
(13.2)
которую называют формулой перекрытий, или формулой включений и исключений. Чаще эту формулу записывают в следующем виде.
Обозначим символом  свойство A, которым данные предметы не обладают. Тогда число предметов, не обладающих ни одним из указанных свойств, будет равно
свойство A, которым данные предметы не обладают. Тогда число предметов, не обладающих ни одним из указанных свойств, будет равно
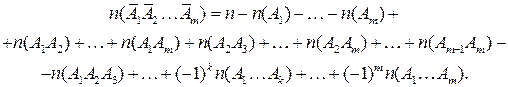 (13.3)
(13.3)
Здесь алгебраическая сумма распространена на все комбинации свойств A1,…,Am (без учета их порядка), причем знак «+» ставится, если число учитываемых свойств четно, и знак «–», если это число нечетно. Название формулы (13.2) как формулы включений и исключений связано с тем, что сначала исключаются все предметы, обладающие хотя бы одним из свойств, потом включаются предметы, обладающие по крайней мере двумя из этих свойств, после этого исключаются предметы, обладающие по крайней мере тремя свойствами, и т.д.
В случае трёх свойств формулы (13.2) и (13.3) примут вид:
 , (13.4)
, (13.4)
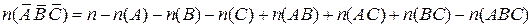 . (13.5)
. (13.5)
Пример 13.1. В научно-исследовательском институте работают 67 человек. Из них 47 знают английский язык, 35 – немецкий язык и 23 – оба языка. Сколько человек в институте не знают ни английского, ни немецкого языков?
Решение. Обозначим через A – сотрудников, знающих английский язык, через B – сотрудников, знающих немецкий язык. По условию

Тогда
 .
.
Итак, 8 человек не знают ни английского, ни немецкого языка.
Пример 13.2. Сколько можно сделать перестановок из n элементов, в которых данные два элемента a и b не стоят рядом? Данные три элемента a, b, c не стоят рядом (в любом порядке)? Никакие два из элементов a, b, c не стоят рядом?
Решение. Если a и b стоят рядом, то их можно объединить в один знак. Учитывая, что a и b можно переставлять местами, получаем  перестановок, в которых a и b стоят рядом. Тогда в
перестановок, в которых a и b стоят рядом. Тогда в

случаях они не стоят рядом. Точно также получаем, что a, b, c не стоят рядом
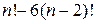
случаях. Никакие два из элементов a, b, c не стоят рядом

случаях (формула включений и исключений).
Пример 13.3. Сколькими способами можно посадить рядом 3 англичан, 3 французов и 3 немцев так, чтобы никакие три соотечественника не сидели рядом?
Решение. 9 человек можно пересаживать 9! способами. Найдём, во скольких перестановках 3 англичанина сидят рядом. Все такие перестановки получаются из одной пересаживанием между собой англичан (3! способов) и 3 французов и 3 немцев и компании из трех англичан (7! способов). Всего получаем 3!7! перестановок. Во стольких же перестановках сидят рядом 3 французов и во стольких же – 3 немцев. Далее, в (3!)25! перестановках сидят рядом трое англичан и трое французов, а также трое англичан и трое немцев, трое французов и трое немцев. И, последнее, в (3!)4 перестановках сидят рядом и англичане, и французы, и немцы. В результате, по формуле включений и исключений, находим
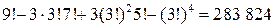 способа.
способа.
Упражнения
13.1. На загородную прогулку поехали 92 человека. Бутерброды с колбасой взяли 47 человек, с сыром – 38 человек, с ветчиной – 42 человека, и с сыром и с колбасой – 28 человек, и с колбасой и с ветчиной – 31 человек, и с сыром и с ветчиной – 26 человек. Все три вида бутербродов взяли 25 человек, а несколько человек вместо бутербродов захватили с собой пирожки. Сколько человек взяли с собой пирожки?
Ответ: 25.
13.2. В отделе научно-исследовательского института работают несколько человек, причем каждый из них знает хотя бы один иностранный язык, 6 человек знает английский язык, 6 – немецкий, 7 – французский, 4 знают английский и немецкий, 3 – немецкий и французский, 2 – французский и английский, 1 человек знает все три языка. Сколько человек работает в отделе? Сколько из них знают только английский язык? Сколько человек знают только один язык?
Ответ: По формуле включений и исключений число работающих равно 6+7+6–4–3–2+1=11. Только английский знают 6–4–2+1=1, только немецкий 6–4–3+1=0, только французский 7–3–2+1=3. Т.о., только один язык знают 4 человека.
13.3. Староста одного класса дал следующие сведения об учениках: «В классе учатся 45 школьников, в том числе 25 мальчиков. 30 школьников учатся на хорошо и отлично, в том числе 16 мальчиков. Спортом занимаются 28 учеников, в том числе 18 мальчиков и 17 школьников, учащихся на хорошо и отлично. 15 мальчиков учатся на хорошо и отлично и занимаются спортом». Покажите, что в этих сведениях есть ошибка.
Ответ: Число школьников, которые не учатся на хорошо и отлично и не занимаются спортом, равно 45–30–28+17=4. Число мальчиков, которые не учатся на хорошо и отлично и не занимаются спортом, равно 25–16–18+15=6, т.е. их больше 4, что не может быть.
13.4. В лифт сели 8 человек. Сколькими способами они могут выйти на четырех этажах так, чтобы на каждом этаже вышел, по крайней мере, один человек?
Ответ: 8 пассажиров могут распределиться между этажами 48 способами. Из них в 38 случаях на данном этаже, 28 случаях на данных двух этажах и в 1 случае на данных трех этажах не выйдет ни один человек. По формуле включений и исключений получаем  способа.
способа.
13.5. Сколько неотрицательных целых чисел, меньших чем миллион, содержит все цифры 1, 2, 3, 4? Сколько чисел состоит только из этих цифр?
Ответ: По формуле включений и исключений получаем, что все цифры 1, 2, 3, 4 содержат 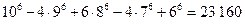 чисел. Только из цифр 1, 2, 3, 4 состоят
чисел. Только из цифр 1, 2, 3, 4 состоят  чисел.
чисел.
АЛГЕБРА СОБЫТИЙ
Одним из основных понятий теории вероятностей является понятие случайного события. Под событием понимается любое явление, которое происходит в результате осуществления определенного комплекса условий и которые можно неоднократно повторять. Осуществление этого комплекса условий называют экспериментом (опытом, испытанием, наблюдением). Таким образом, любое событие в теории вероятностей рассматриваются как исход некоторого эксперимента. Поэтому события часто называют исходами. Например, бросание кубика можно считать испытанием, которое можно неоднократно повторять, а полученный результат – исходом испытания.
Событие называется случайным, если оно при одних и тех же условиях может как произойти, так и не произойти. Случайными будут, например, события: а) при подбрасывании игрального кубика выпадет 6 очков; б) при выстреле в мишень пуля попадет в «десятку»; в) по пути в школу вы встретите черную кошку.
Чтобы говорить о случайности или неслучайности какого-то события, нужно иметь возможность неоднократно наблюдать за ним. Недаром каждый из перечисленных примеров начинается со слов «при …» – то есть, при выполнении определенных условий. Эти условия могут создаваться специально или возникать в окружающей нас жизни.
Случайным экспериментом называют комплекс действий или условий, которые можно многократно повторять, а исход, к которому они приводят, заранее непредсказуем. С примерами случайных экспериментов вы, наверняка, сталкивались и раньше: а) подбрасывание монеты или игрального кубика; б) проведение лотереи; в) стрельба по мишени; г) подъем уровня воды во время весеннего половодья. Последний пример показывает, что случайные эксперименты может совершать и сама природа – в этом случае нам остается лишь наблюдать за их исходами.
Остановимся еще раз на двух важнейших свойствах случайного опыта - непредсказуемости и повторяемости.
Первым важным свойством случайного опыта является его непредсказуемость. Мы не можем заранее предсказать на какую сторону упадет подброшенная вверх монета или кубик; в какую точку мишени попадет пуля.
Вторым важным свойством случайного опыта является его повторяемость: мы (или природа) можем повторять опыт неограниченное число раз в одних и тех же (или очень близких) условиях.
Теория вероятностей не изучает уникальные эксперименты, которые нельзя повторить многократно, даже если их исходы непредсказуемы.
События будем обозначать заглавными буквами латинского алфавита: A, B, C и т.д.
Событие называется невозможными, если при проведении данного случайного эксперимента никогда не происходит. Например, события: а) при подбрасывании игрального кубика выпадет 7 очков; б) при подбрасывании трех монет число орлов окажется равно числу решек, являются, очевидно, невозможными.
Событие называется достоверным, если при проведении данного случайного эксперимента оно обязательно произойдет. Например, события: а) при подбрасывании игрального кубика выпадет меньше 7 очков; б) при подбрасывании трех монет число орлов окажется не равно числу решек, являются, очевидно, достоверными.
События A и B называются несовместными, если наступление одного из них исключает возможность появления другого. Например, при подбрасывании монеты могут наступить два события: выпадет «орел» или «решка». Однако, одновременно эти события, при одном подбрасывании, появится не могут. Если в результате испытания возможно одновременное появление событий A и B, то такие события называются совместными. Например, выпадение чётного числа очков при подбрасывании игральной кости (событие А) и числа очков, кратного трем (событие В) будут совместными, ибо выпадение шести очков означает наступление и события А, и события В.
Возможными исходами случайного эксперимента называются все взаимоисключающие друг друга варианты, одним из которых он должен завершиться. В результате эксперимента всегда происходит один и только один из его исходов. То есть, с одной стороны, в одном эксперименте не могут произойти сразу два исхода, с другой - эксперимент не может завершиться вообще без всякого исхода. Исходы эксперимента называют элементарными, если их нельзя поделить на более простые. Элементарные исходы в теории вероятностей называют еще элементарными событиями.
Заметим, что число возможных исходов случайного опыта может быть любым – от двух до бесконечности. Например, опыт с монетой имеет всего два возможных исхода (орел и решка), а опыт с кубиком – шесть. Но далеко не во всех случаях все возможные исходы опыта столь очевидны.
Из коробки с одним белым и двумя черными шарами вытаскивают наугад один шар. Сколько возможных исходов у этого опыта? Можно сказать два: шар окажется либо белым, либо черным. А можно сказать три: белый, черный-1, черный-2. И то, и другое правильно, просто во втором случае исходы выбраны более элементарными, а сам опыт описывается ими более детально.
Любое неэлементарное событие может наступить при различных исходах опыта. Все такие исходы называют благоприятными для этого события. Благоприятные они в том смысле, что приводят к его наступлению. Например, для случайного события «На кубике выпадет четное число очков» благоприятными исходами будут 2, 4 и 6.
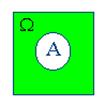
Если обозначить множество всех возможных исходов опыта большой греческой буквой  (читается омега), то каждый исход можно рассматривать как элемент этого множества
(читается омега), то каждый исход можно рассматривать как элемент этого множества  , а любое случайное событие A – как его подмножество
, а любое случайное событие A – как его подмножество 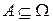 , состоящее из благоприятных для него исходов.
, состоящее из благоприятных для него исходов.
При этом невозможное и достоверное события получаются как два частных случая таких подмножеств: невозможному событию соответствует пустое множество исходов  ; достоверному событию соответствует множество всех исходов опыта
; достоверному событию соответствует множество всех исходов опыта  .
.
Итак, для любого случайного события A все исходы эксперимента делятся на два множества: благоприятные для этого события и все остальные, которые можно назвать неблагоприятными для него. Если рассматривать событие A как подмножество в множестве всех возможных исходов, то оно будет состоять из благоприятных исходов.
Например, выниманию из колоды одной карты можно поставить в соответствие множество элементарных событий (карт) W с 36 исходами. Тогда событию B={вынут туз} соответствует подмножество B={туз пик, туз крести, туз буби, туз червы}.
Пример 14.1. Пусть эксперимент состоит в подбрасывании один раз игральной кости. Обозначим через X число выпавших очков. Построить пространство элементарных событий и указать состав подмножеств, соответствующих следующим событиям: A={X кратно3}, B={X – нечетно}, C={X < 7}, D={X > 7}.
Решение. Очевидно, что за элементарные события здесь лучше всего взять события: {1}, {2}, {3}, {4}, {5}, {6}, которые образуют полную группу несовместных событий. При помощи этих элементарных событий можно легко описать все перечисленные в задаче события:
A={3;6}, B={1;3;5}, C=, D=Æ.
Над событиями можно совершать те же самые операции, что и для множеств. В частности:
Произведением AB событий A и B называют событие, которое происходит тогда и только тогда, когда имеют место оба события A и B одновременно. Например, событие C={вынут туз черви} является произведением событий A и B, где A={вынута карта червонной масти}, а B={вынут туз}.
Суммой A+B событий A и B называют событие, которое происходит только тогда, когда имеет место либо событие A, либо событие B, либо оба вместе.
Разность A–B событий A и B называют событие, которое происходит только тогда, когда имеет место событие A, но не имеет место событие B.
Событие  называется противоположным к событию
называется противоположным к событию 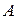 , если оно происходит тогда и только тогда, когда не происходит
, если оно происходит тогда и только тогда, когда не происходит 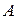 . Другими словами, противоположное событие состоит из тех элементарных исходов множества
. Другими словами, противоположное событие состоит из тех элементарных исходов множества  , при которых событие
, при которых событие 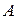 не происходит, т.е.
не происходит, т.е. 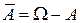 .
.
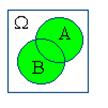
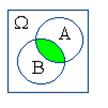
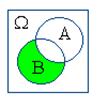
Действия над событиями становятся более наглядными, если придать им геометрическую интерпретацию в виде диаграмм Эйлера-Венна:
| 
| 
| 
| 
|
| A+B | AB | A–B | B–A | 
|
Пример 14.2. Эксперимент состоит в подбрасывании двух игральных костей. Обозначим через X сумму очков, выпадавших на обеих костях. Описать следующие события A+B, AB, A–B, B–A, если A={X кратно трем}={3;6;9;12}и B={X нечетно}={3;5;7;9;11}. Тогда
| A+B={3;5;6;7;9;11;12}, | A–B={6;12}, |
| AB={3;9}, | B–A={5;7;11}. |
Пример 14.3. Пусть имеется колода карт, из которой вынимается одна карта. Описать события AB, 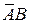 , A+B, A–B,
, A+B, A–B, 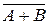 , если A={вынутая карта – туз}, B={вынутая карта – черви}.
, если A={вынутая карта – туз}, B={вынутая карта – черви}.
Ответ:
AB = {вынутая карта – червовый туз},
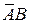 = {вынутая карта – червовая, но не туз},
= {вынутая карта – червовая, но не туз},
A+B = {вынутая карта – либо туз, либо черви},
A–B = {вынутая карта –туз, но не черви},
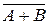 = {вынутая карта – не туз и не черви}.
= {вынутая карта – не туз и не черви}.
Используя операции над событиями, можно описывать более сложные события. Например, пусть A, B, C – три события, наблюдаемые в некотором эксперименте. Используя алгебру событий, опишем событие, произошло только событие А. Это означает, произошло событие A, но события B и С не произошли. Это можно записать следующим образом
 .
.
Аналогично, можно описать события: произошло только одно событие, не важно какое или: произошло хотя бы одно событие. Все это можно коротко записать так
 ,
,
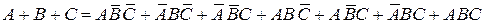 .
.
Пример 14.4. Пусть ёлочная гирлянда имеет следующий вид
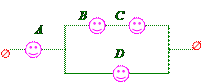
Опишите событие, что: а) цепь будет работать (т.е. загорится хотя бы одна лампочка), б) имеется разрыв цепи (т.е. ни одна лампочка не загорится).
Ответ: а) Для того чтобы цепь работала, нужно чтобы работала лампочка А и (операция умножения) верхняя или нижняя ветка гирлянды (операция сложения). Верхняя ветка будет работать, если будут работать и лампочка B, и лампочка C (операция умножения). Используя алгебру событий всё это можно записать в виде формулы:
 .
.
б) Для того чтобы цепь не работала, нужно чтобы не работала лампочка А или (операция сложения) верхняя и нижняя ветка гирлянды (операция умножения). Верхняя ветка не будет работать, если не будут работать или лампочка B, или лампочка C (операция сложения). Используя алгебру событий всё это можно записать в виде формулы (для обозначения, что лампочка не работаем мы будем использовать символ противоположного события):
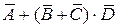 .
.
Упражнения
14.1. Имеется колода карт. Вынимается одна карта. Опишите события  и
и  если A={карта пиковой масти}, B={карта – дама}.
если A={карта пиковой масти}, B={карта – дама}.
Ответ:  ={вынутая карта – либо не пики, либо не дама},
={вынутая карта – либо не пики, либо не дама}, 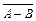 ={вынутая карта – либо не пики, либо дама}.
={вынутая карта – либо не пики, либо дама}.
14.2. В урне находится 12 шаров. Все они пронумерованы от 1 до 12. Опишите событие  и (A–B)+(B–A), если A={шар с номером кратным 3}, B={шар с номером меньше 5}.
и (A–B)+(B–A), если A={шар с номером кратным 3}, B={шар с номером меньше 5}.
Ответ: 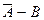 ={5, 7, 8, 10, 11}, (A–B)+(B–A)={6, 9, 12, 1, 2, 4}.
={5, 7, 8, 10, 11}, (A–B)+(B–A)={6, 9, 12, 1, 2, 4}.
14.3. В урне находится 12 шаров. Все они пронумерованы от 1 до 12. Опишите событие  и
и  , если А={шар, с номером кратным 4}, B={шар, с номером не меньше 6}.
, если А={шар, с номером кратным 4}, B={шар, с номером не меньше 6}.
Ответ: 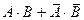 ={8, 12, 1, 2, 3, 5},
={8, 12, 1, 2, 3, 5},  ={8, 12}.
={8, 12}.
14.4. Имеется электрическая цепь. Опишите, что: а) цепь будет работать, б) имеется разрыв цепи.
1)  2)
2) 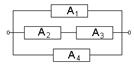 .
.
Ответ: 1) 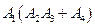 ,
,  ;
;
2) 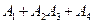 ,
,  .
.
14.5. Имеется электрическая цепь. Опишите, что: а) цепь будет работать, б) имеется разрыв цепи.
1) 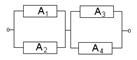 2)
2)  .
.
Ответ: 1)  ,
,  ;
;
2) 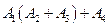 ,
,  .
.