 |
|
ЛОКАЛЬНАЯ ТЕОРЕМА МУАВРА - ЛАПЛАСА
И ФОРМУЛА ПУАССОНА
Если вероятность наступления события А в каждом испытании по-стоянна, то вероятность того, что в n независимых испытаниях оно состоится т раз, при любом числе испытаний n определяется формулой Бернулли. Во всех рассмотренных примерах число испытаний было небольшим. Если же число испытаний велико, то вычисления искомых вероятностей по формуле Бернулли становятся очень громоздкими.
Например, если вероятность поражения мишени при одном выстреле равна 0,4, то вероятность того, что при 600 выстрелах мишень будет поражена 250 раз, согласно формуле Бернулли можно получить формальный ответ. Но нахождение численного значения его даже с помощью таблиц логарифмов связано с серьезными трудностями. Кроме того, вычисления оказываются неточными, так как при сложении логарифмов, которые являются приближенными числами, ошибка накапливается. Поэтому, когда число испытаний велико, для нахождения вероятностей, нецелесообразно применять формулу Бернулли. Нужны формулы, по которым достаточно точные значения вероятностей находились бы при сравнительно несложных вычислениях. Поставленная задача имеет положительное решение. Такими формулами являются формулы Муавра — Лапласа и Пуассона,
Локальная теорема Муавра — Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в n независимых испытаниях событие А наступит m раз, приближенно равна:
 где функция f(x) определяется равенством:
где функция f(x) определяется равенством: 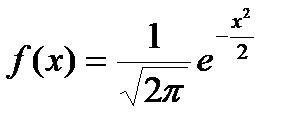
Формула называется формулой Муавра — Лапласа. С возрастанием n относительная точность значений вероятностей, получаемых по ней, возрастает. В этом и заключается содержание локальной теоремы Муавра — Лапласа.
Для упрощения расчетов, связанных с применением формулы, составлена таблица значений функции f(x). Пользуясь этой таблицей, необходимо иметь в виду свойства функции, а именно:
1. Функция f(х) является четной, т. е. f (-х) = f (х). Поэтому в таблице приведены значения функции лишь для положительных значений аргумента.
2. Функция f(х) — монотонно убывающая при положительных зна-чениях х. Предел f(х) при равен нулю.
3. Если х > 5, то можно считать, что . Функция f(х) уже при х = 5 очень мала: f(5)=0,0000015. Поэтому таблица значений функции f(х) не продолжена для значений х > 5.
Пример. Найти вероятность того, что при 600 выстрелах мишень будет поражена 250 раз, если вероятность поражения мишени при одном выстреле равна 0,4.
Решение. P=f(0.833)/12=0.0235.
Пример. Вероятность рождения мальчика равна 0,515. Найти вероят-ность того, что из 200 новорожденных будет 95 девочек.
Решение. Поскольку необходимо найти вероятность того, что будет 95 девочек, то в формулах через р должна обозначаться вероятность рождения девочки, при этом р = 1—0,515 == 0,485. При n = 200, р == 0,485 и q = 0,515 значение х, соответствующее m= 95, равно –0,283. По таблице находим, что f(0,283) = 0,3833. Поэтому окончательно имеем: P=0.3833/7.068=0.054.
Если вероятность р наступления события в отдельном испытании близка к нулю, то даже при большом числе испытаний т, но при не-большой величине произведения np, получаемые по формуле Муавра — Лапласа значения вероятностей оказываются недостаточно точными и возникает потребность в другой приближенной формуле для таких случаев.
Теорема. Если вероятность р наступления события А в каждом испытании постоянна, но мала, число независимых испытаний n достаточно велико, но произведение остается небольшим, то вероятность того, что в этих испытаниях событие А наступит m раз,
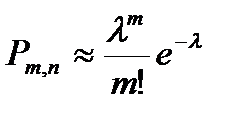
Формула называется формулой Пуассона. Для упрощения расчетов, связанных с применением ее, составлена таблица значений функции Пуассона.
Пример. Пусть вероятность изготовления нестандартной детали равна 0,004. Найти вероятность того, что среди 1000 деталей окажется пять нестандартных.
Решение. Здесь n = 1000, р = 0,004, а = nр = 1000 • 0,004= 4. Все три числа удовлетворяют требованиям только что доказанной теоремы, а поэтому для нахождения вероятности искомого события применяем фор-мулу Пуассона. По таблице значений функции Пуассона при =4 и m = 5 сразу получаем: P=0,1563.
4.Отклонение относительной частоты от постоянной вероятности.
Случайные величины
1Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.
Законом распределения случайной дискретной величины (X) называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины (x1,x2,...xn) и соответствующими им вероятностями (p1,p2,... ,pn). При этом события (x1,x2,...xn) образуют полную группу (т.е. появление одного из них является достоверным событием), что означает
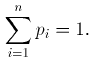
Про случайную величину X в таком случае говорят, что она подчинена данному закону распределения.
Простейшей формой задания этого закона является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:
Возможное значение X
X1 Х2 ... Хn
Вероятность Р1 Р2 ... Рn
Такая таблица называется таблицей распределения (вероятностей) случайной величины X.
Пример 1. Число X очков, выпадающее на верхней грани игральной кости, есть дискретная случайная величина с таблицей распределения вероятностей
X 1 2 3 4 5 6
p 1/6 1/6 1/6 1/6 1/6 1/6
Пример 2. Из урны, в которой лежат 2 белых и 8 черных шаров, последовательно вынимают шары до тех пор, пока не появиться черный шар. Число Y вынутых при этом шаров есть дискретная случайная величина. Составим закон распределения ее вероятностей.
Решение. Возможными значениями величины Y являются, очевидно, 1, 2, 3. Событие Y = 1 означает, что уже первый шар будет черным; поэтому его вероятность равна
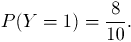
Событие Y = 2 означает, что приходится вынуть два шара, причем первый будет белым, а второй - черным. По правилу умножения вероятностей получим
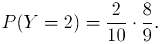
Наконец, событие Y = 3 означает, что первые два шара оказались белыми, а третий - черным. Последовательно применяя (6.9) два раза, получим
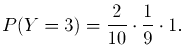
последний сомножитель 1 означает, что появление третьим шаром черного при условии, что до этого вынимались два белых является достоверным событием.
Таким образом, таблица распределения вероятностей имеет вид

Сумма всех найденных вероятностей, согласно (1) равна единице: 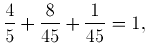
ет служить для контроля произведенных вычислений.
Пример 3. Дискретная случайная величина X имеет закон распределения
Построить закон распределения случайной величины Y = X2 + 1.
Решение. Значение Y = 1 наступает только в случае, когда X = 0, с вероятностью 0.3. Значение 2 величина Y принимает, если величина X принимает значения -1 или 1 с вероятностями 0.2 и 0.3 соответственно. Тогда эти вероятности необходимо сложить, что даст P(Y = 2) = 0.5. Аналогично вероятность того, что Y = 5 будет равна 0.1 + 0.1 = 0.2. Следовательно закон распределения случайной величины Y = X2 + 1 имеет вид
Y 1 2 5
Р 0.3 0.5 0.2
Некоторые законы распределения вероятностей дискретных случайных величин часто встречаются при решении различных задач. Такие законы распределения получили специальные названия: геометрическое распределение, биномиальное распределение, распределение Пуассона и т.д.
2 Мат ожидание. В тетради 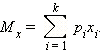
3. дисперсия случайной величины. Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания.
4.Функция распределения. В тетради.
5.непрерывные случайные величины, плотность вероятности.