 |
|
Функции случайных величин
Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайной величины Х и записывают Y = j(х).
Если Х – дискретная случайная величина, то возможные значения Y находят из равенства уi= j(xi), где xi – возможные значения Х; вероятности возможных значений Y находят из равенства P{Y = yi} = P{X = xi}. Если среди возможных значений Y встретятся одинаковые, то следует сложить вероятности тех возможных значений Х, при которых Y принимает одинаковые значения.
Если Х – непрерывная случайная величина с плотностью вероятности fx(x), а у = j(х) – дифференцируемая строго монотонная функция, обратная функция которой х = y(у) однозначна, то плотность вероятности fy(y) случайной величины Y определяетcя по формуле 
.
Если функция Y= j(х) не монотонная в интервале возможных значений Х, то следует разбить этот интервал на такие интервалы, в которых функция j(х) монотонна, найти плотность распределения Y для каждого интервала монотонности, а затем представить fy(y) в виде их суммы 
.
Числовые характеристики функции случайной величины можно найти, не определяя закона распределения у = j(х), по формулам
;
для дискретных случайных величин и
;
для непрерывных случайных величин.
Аналогично находятся начальные и центральные моменты любого порядка, а также числовые характеристики функции нескольких случайных аргументов (подробнее см. [8]).
Если функция j(Х1, Х2, …, Хn) – линейная, т.е. 
, то 
; 
,
где Кij – корреляционный момент случайных величин Хiи Xj (в этом случае не требуется знание закона распределения случайных аргументов).
Числовые характеристики непрерывно дифференцируемых функций могут быть вычислены приближенно методом линеаризации (т.е. удерживая в разложении функции в ряд Тейлора только линейные члены):
а) для функции одного случайного аргумента Y = j(х)
M[Y] » j(M[x]); D[Y] » [j’(M[x])]2D[x];
б) для функции нескольких случайных аргументов
Y = j(Х1, Х2,…, Хn)
М[Y] » j(M[Х1], M[Х2], …,M[Хn]),
,
где Кij – корреляционный момент для случайных величин Хiи Xj, а через 
обозначены производные, вычисленные для значений аргументов, равных их математическим ожиданиям.
Если случайные величины взаимно не коррелированны, то 
.
17.1. Дискретная случайная величина Х имеет ряд распределения:
| x | 
| 
| 
| 
| 
| |
| р | 0,1 | 0,2 | 0,1 | 0,2 | 0,3 | 0,1 |
Найти закон распределения функции z = sinx, вычислить M[Z]
и D[Z].
17.2. Непрерывная случайная величина Х имеет плотность вероятности f(x). Выразить функцию распределения и плотность вероятности случайной величины Z = x2 через функцию и плотность распределения Х.
17.3. Независимые случайные величины Х и Y распределены показательно с параметрами a и b соответственно a ¹ b. Найти плотность вероятности случайной величины Z = X + Y.
17.4. Система состоит из двух независимых элементов, соединенных последовательно в смысле надежности. Время безотказной работы каждого из элементов имеет показательное распределение с параметрами a1 и a2 соответственно. Найти функцию распределения времени безотказной работы системы.
Указание. T = min{T1, T2} , где Ti – время безотказной работы i-го элемента.
17.5. Система состоит из двух независимых элементов, соединенных параллельно в смысле надежности. Время безотказной работы каждого из элементов имеет показательное распределение с параметрами a1 и a2 соответственно. Найти функцию распределения времени безотказной работы системы.
Указание. T = max{T1, T2} , где Ti – время безотказной работы i-го элемента.
17.6. Непрерывная случайная величина Х имеет плотность 
Найти математическое ожидание и дисперсию случайной величины Y = sinX
17.7. Две независимые случайные величины Х и Y имеют следующие законы распределения:
| х | y | ||||||
| р | 0,2 | 0,5 | 0,3 | р | 0,4 | 0,6 |
Найти закон распределения случайной величины Z = X–2Y и проверить свойства математических ожиданий и дисперсией M[Z] = M[X]–2M[Y], D[Z] = D[X]+4D[Y].
17.8. Результат измерения ребра куба есть случайная величина Х, дисперсия которой (характеристика точности измерительного прибора) равна 0,0001 мм2. Определить приближенно дисперсию объема куба Y, вычисляемого по результатам измерений, если измеряемые прибором длины заключены в пределах от 1 мм до 2 мм.
17.9. Начальная фаза j малых свободных колебаний груза на пружине связана с начальным смещение Х, начальной скоростью v и свободной круговой частотой колебаний w формулой 
. Начальные условия задаются независимо с разбросом относительно номинальных значений mx = 2 см и mv = 2 см/с, который характеризуется средними квадратическими отклонениями sх = 0,4 см, sv = 0,3 см/с. Вычислить приближенно среднее квадратическое отклонение начальной фазы при w = 10.
17.10. Размеры двух шкивов (А и В) характеризуются математическими ожиданиями радиусов (номинальные размеры) 
, 
и дисперсиями исполнения D[rA] = 0,04, D[rB] = 0,01. Найти приближенно математическое ожидание и среднее квадратическое отклонение передаточного числа 
от шкива В к шкиву А.
 |
17.11. Линейная размерная цепь включает три составляющих размера Х, Y, Z и замыкающий размер Т. Соответствующие номинальные размеры равны: 
= 100 мм, 
= 50 мм,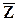 
= 250 мм. Кроме того, известно, что sх = 1 мм, sу = 1 мм, sz = 2 мм. Размер Z получается независимой от Х и Y обработкой, а размеры Х и Y получаются согласно технологии связанными, причем rxy = 0,9. Найти М[T], s[T].
 |
 |
 |
17.12. Кинематика кривошипно-кулисного механизма определяется размерами h и r, при исполнении которых допускаются погрешности, характеризующиеся средними квадратическими отклонениями sh и sr . Найти номинальный максимальный угол отклонения кулисы jmax от вертикального положения и среднее квадратическое отклонение реального угла, если номинальные размеры r и h равны соответственно 141,4 мм и 200 мм, sh = 1 мм, sr = 2 мм.
Указание. 
.
17.13. Пусть Х – непрерывная случайная величина с плотностью f(x). Выразить плотность вероятности функции z = aX+b (a > 0) через f(x).
17.14. Две независимые случайные величины Х и Y имеют следующие законы распределения:
| х | –4 | y | ||||||
| р | 0,2 | 0,6 | 0,2 | р | 0,5 | 0,2 | 0,3 |
Найти закон распределения случайной величины Z = 2X–Y и проверить свойства математических ожиданий и дисперсией M[Z] = 2M[X]–M[Y], D[Z] = 4D[X]+D[Y].
17.15. Колебательная система состоит из груза с массой m = 1 кг и пружины с жесткостью k = 4 Н/м. Она выводится из состояния равновесия случайным смещением Х0, распределенным равномерно на отрезке [–0,1 м; 0,1 м] и случайным Р0 = mv0, математическое ожидание которого 
= 2 кг м/с, среднее квадратическое отклонение 
= 1 кг м/с. Найти приближенно математическое ожидание и дисперсию амплитуд малых свободных колебаний.
Указание. Амплитуда свободных колебаний связана с начальными условиями соотношением 
.
17.16. При измерении стороны квадрата линейкой, цена деления которой равно 2D, допускается погрешность округления. Пусть длина стороны квадрата равна а. Найти плотность вероятности случайной величины S – результата вычисления площади квадрата. Вычислить математическое ожидание и дисперсию S и сравнить полученные точные значения с приближенными, определенными по методу линеаризации.
Указание. Результат измерения Х есть случайная величина, равномерно распределенная на отрезке [а–D; а+D].
17.17. По сторонам прямого угла xОy концами скользит линейка АВ длины l, занимая случайное положение, причем все значения абсциссы X её конца А на оси Ох в пределах от 0 до l одинаково вероятны. Найти математическое ожидание расстояния R от начала координат до линейки.