Главная | Обратная связь

ЧАСТЬ 5. ЭЛЛИПТИЧЕСКИЕ КРИВЫЕ НАД КОНЕЧНЫМ ПОЛЕМ.

В данном пособии рассматриваются только задачи, решаемые в конечной аддитивной группе точек эллиптической кривой над простым конечным полем характеристики p>3.

Конечной группой точек эллиптической кривой называют совокупность точек с целочисленными координатами удовлетворяющих короткой аффинной форме однородного уравнения Вейерштрасса над конечным полем характеристики p [3]:

Кривая также характеризуется:

дискриминантом

и j-инвариантом .

В данной аддитивной группе точек определены две операции – сложение и удвоение, которые выполняются в соответствии с групповым законом:

Пусть P₁(x₁, y₁), P₂(x₂, y₂) и, если P₃(x₃, y₃) = P₁ + P₂ ≠ O, то координаты x₃, y₃ вычисляются как:

где при

а при

При создании криптосистем на основе эллиптических кривых важно знать порядок группы точек эллиптической кривой. Он характеризует стойкость системы и является одним из ее параметров.

На практике порядок группы точек эллиптической кривой и ее циклической подгруппы находится при помощи алгоритма Шуфа [5], который в данном пособии не приводится. Определим порядок группы точек методом прямого перебора на примере кривой над полем характеристики , характеризуемой уравнением [11]:

Ее дискриминант:

, - кривая не аномальная и не суперсингулярная.

Для каждого элемента поля F_p вычислим y²:

При помощи вычисления символа Лежандра по упрощенной зависимости:

определим возможность извлечения квадратного корня.

В случае – на кривой нет целочисленных точек с таким x.

В случае – мы нашли нулевую точку ( x, 0).

В случае произведем извлечение квадратного корня по упрощенной методике и определим:

Результаты вычислений сведены в таблицу 5.

Таблица 5

x
y1	y2
		22(-1)	-	-
				-
		22(-1)	-	-
		22(-1)	-	-
		22(-1)	-	-
		22(-1)	-	-
		22(-1)	-	-
		22(-1)	-	-
		22(-1)	-	-
		22(-1)	-	-

Из таблицы видно, что количество точек с целочисленными координатами Q = 27. 27 – составное число, поэтому в группе существует несколько циклических подгрупп.

Задача 5.1. Для заданной эллиптической кривой E над конечным полем и ее точек P₁ и P₂ , осуществить удвоение точки P₁ и сложить результат с точкой P₂. Проверить принадлежность результата к группе точек эллиптической кривой.

Пример решения

Дано: P1(18, 20), P2(7,11)	Решение:
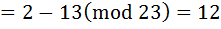
Найти: Q = [2]P1 + P2 Проверить: принадлежность Q эллиптической группе E

;

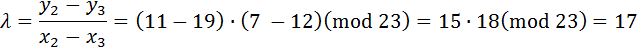
Умножение точки эллиптической кривой на скаляр производится с применением схемы Горнера аналогично бинарному модульному экспоненцированию в задаче 2.3. Задача 5.2. Для заданной эллиптической кривой E над конечным полем, ее точки P и числа x , осуществить умножение [x]P, воспользовавшись схемой Горнера. Проверить принадлежность результата к группе точек эллиптической кривой.
Дано: P (1, 16); x = 9	Решение:
Найти: Q = [9]P Проверить: принадлежность Q группе E

 

Ниже приведены примеры реализации криптосистем на основе эллиптических кривых.