 |
|
Седловая тоска и чистые стратегии.
Если I(с чертой сверху)=I(с чертой снизу), то говорят что в игре есть седловая точка, т.е. maximinj(W(I,j))=minjmaxi(W(I,j)). В такой ситуации одной из сторон нет смысла отклонятся от своей минимаксной стратегии, а следовательно игра устойчива к информированности о действиях противника. Применение игроками одной и той же стратегии приводит к эффективному результату лишь тогда, когда в игре есть силовая точка. В иных случаях игрокам необходимо менять чистые стратегии от шага к шагу в зависимости от действий противника. Правило последовательного применения разных чистых стратегий может быть сформулировано в относительных частотах.
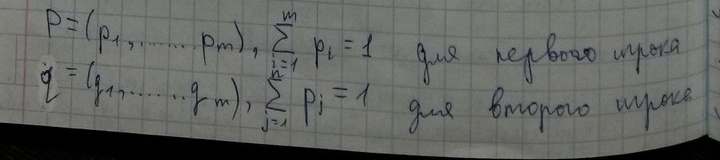
19. Смешанные стратегии.
Также относительные частоты называются смешанными стратегиями. Когда количество шагов стремится к бесконечности, то согласно закону больших чисел можно вычислить средний выигрыш игроков в виде мат. Ожидания.

В этом случае можно вести речь о седловой точке игры в смешанных стратегиях, когда выполняется следующее выражение:

P*,q* таких что имеет место седловая точка, называемая решением игры в смешанных стратегиях. Применяя эти стратегии оба игрока получают наиболее выгодный результат. Ниже приведем теоремы котоые справедливы для оптимальных смешанный стратегий.
1. Для того чтобы число I явл. Ценой игры с матрицей Аmin=(aij), a p* q* явл. Оптимальными стратегиями необходимо и достаточно, чтобы 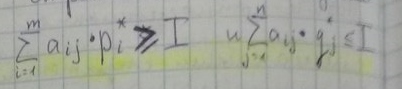
2. Если один из игроков применяет оптимальную стратегию, то его выигрыш равен цене игры вне зависимости от того, с какими частотами будет применять второй игрок свои чистые стратегии, в том числе вошедшие в оптимальную смешанную стратегию
3. Всякая конечная игра с нулевой суммой имеет решение в чистых стратегиях
Игры с природой.
Довольно часто экономические системы, отличающиеся своей уникальностью, необходимо оценить с точки зрения эффективности их работы. Для оценки эффективности их работы существуют критерии Байеса, Лапласа, Гурвица, Сэвиджа, Вальда. В основе критерия Лапласа лежит предположение : если вероятность состояния природы равноподобны, то их можно считать равновероятными. Формула для расчета систем по критерию Лапласа
Оптимальная стратегия по этому критерию находится след. Образом

Критерий Вальда гарантирует опр. Выигрыш при наихудших условиях. Критерий основывается на том, что если состояние обстановки неизвестно, то нужно поступать самым осторожным образом, ориентируясь на минимальное значение эффективности каждой системы. В каждой строке матрицы эффективности находятся минимальные значения по различным состояниям обстановки. K(Ai)=min kij, i=1,…,m. оптимальной считается система из строки с максимальным значением эффективности. Kopt= max{K(Ai), i=1,…,m} . по критерию базиса за оптимальную применяется та стратегия(чистая), при которой максимизируется средний выигрых или минимизируется средний риск. Для расчета системы по критерию базиса необходимо знать возможные состояния системы. Если таковы ищвестны, то систему по критерию базиса невозможно просчитать.
Если «весы» в состоянии системы равны, то по критерию базиса становится равным критерий Лапласа.

Согласно данному критерию при оценке систем не разумно как осторожность так и азарт. А следует учитывать самые высокие и низкие значения эффективности, занимать промежуточную позицию.