Главная | Обратная связь

Основні теоретичні відомості

Нехай матеріальна точка бере участь одночасно у двох взаємно перпендикулярних коливаннях однакової частоти. Ці коливання описуються рівняннями:

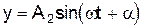, (1) , (2)

де x, y – зміщення матеріальної точки вздовж осей OX та OY відповідно; А₁, А₂ – амплітуди коливань; 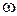– циклічна частота; t – час; – різниця фаз коливань, які даються формулами (1) та (2).

Для дослідження процесу додавання двох взаємно перпендикулярних коливань будемо аналізувати траєкторію руху частинок, що є результатом додавання. Рівняння траєкторії – це рівняння, в яке не входить час і яке пов’язує між собою координати X та Y. Виключимо з рівнянь (1) та (2) час, для чого перепишемо ці рівняння

, (3)

. (4)

Тоді, використовуючи співвідношення (3), вираз (4) можна представити так:

(5)

або

. (6)

Рівняння (6) є рівнянням траєкторії руху точки. Це − еліпс, осі якого орієнтовані довільно відносно координатних осей OX і OY .

За різниці фаз, що дорівнює нулю , формула (6) набуває вигляду:

, (7)

що є рівнянням прямої (виродженого еліпса), яка проходить через початок координат (рис. 1)

За різниці фаз дістанемо рівняння прямої (виродженого еліпса), що проходить через початок кооординат і має інший нахил до осі X (рис. 2)

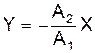. (8)

За різниці фаз і рівняння (6) стає рівнянням еліпса, зведеного до координатних осей (рис. 3).

. (9)

Півосі цього еліпса дорівнюють відповідним амплітудам коливань. Якщо А₁=А₂=А, точка рухається по колу. При рух точка рухається за стрілкою годинника, при – проти. За інших різниць фаз коливань, що додаються, траєкторією руху точки є еліпси, які не “прив’язані” до координатних осей.

Якщо частоти взаємно перпендикулярних коливань неоднакові, траєкторією результуючого руху є складні криві, які називаються фігурами Ліссажу. Найпростіші фігури Ліссажу за різних різниць фаз показані на рис. 4. Чим ближче до одиниці відношення частот коливань, що додаються, тим складніша фігура Ліссажу. Задаючись частотою одного коливання, за формою фігури Ліссажу можна знайти частоту другого коливання. Для цього можна використати рівняння

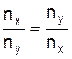, (10)

де n_x, n_y – кількість перетинів фігури Ліссажу з координатними осями, проведеними через центр фігури.

Відомо, що електромагнітні коливання описуються рівняннями, аналогічними виразам (1), (2). Тому дослідження коливальних процесів, зокрема додавання коливань, можна здійснювати і на прикладі електромагнітних коливань. Це зручно зробити, аналізуючи коливання електронного пучка в електронно-променевій трубці осцилографа, що і використовується в даній роботі.