 |
|
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ
Электростатика и постоянный ток (с рисунками)
ЛЕКЦИЯ 1
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ
1. Электрический заряд и его свойства
2. Закон Кулона. Диэлектрическая проницаемость среды
3. Электрическое поле в вакууме
4. Теорема Гаусса и её применение
5. Работа сил электростатического поля.
6. Потенциал электростатического поля. Связь между напряженностью и потенциалом.
7. Потенциал поля системы зарядов.
Еще древние греки знали, что при некоторых условиях тела приобретают особые свойства, которые назвали электрическими (от слова электрон – древнее название янтаря).
Соответственно, процесс приобретения электрических свойств был назван электризацией.
Мерой электрических свойств тела является электрический заряд .
Наука, занимающаяся изучением явлений, обусловленных наличием неподвижных электрических зарядов, называется электростатикой.
Первая научная теория, объясняющая электростатические явления, была разработана американским физиком и философом Франклиным в 18 веке. И хотя принцип существования «электрической жидкости», заложенный в основу его теории оказался неверным, выводы этой теории справедливы и в современной электростатике.
К настоящему моменту установлено, что электрический заряд обладает следующими свойствами:
1) существует два вида электрических зарядов, которые условно названы положительными и отрицательными;
2) электрические заряды взаимодействуют между собой; причем одноимённые заряды отталкиваются, разноимённые притягиваются;
3) суммарный электрический заряд, образующийся в результате любого процесса, равен нулю.
Последнее свойство является проявлением более общей закономерности, называемой законом сохранения заряда.
Назовём электрически изолированной системой – систему, через ограничивающую поверхность которой не перетекает электрический заряд.
Закон сохранения заряда можно сформулировать следующим образом:
Алгебраическая сумма электрических зарядов в электрически изолированной системе есть величина постоянная.
4) Электрический заряд – величина квантованная.
То есть, существует наименьшая порция заряда, которая может самостоятельно существовать в природе.
; 
Кл.
5) Электрический заряд меняет свойства, окружающего его пространства, т.е. создаёт вокруг себя электрическое поле, посредством которого передаётся взаимодействие между зарядами.
Назовём точечным электрическим зарядом заряженное тело, размерами которого в условиях данной задачи можно пренебречь.
Уединённым зарядом будем называть заряженное тело, размеры которого значительно меньше расстояний до других заряженных тел.
Закон, устанавливающий силу взаимодействия между двумя точечными зарядами, был экспериментально открыт в 1785 году французским физиком Кулоном.
Сила взаимодействия двух точечных зарядов в вакууме пропорциональна произведению величин каждого заряда и обратно пропорциональна квадрату расстояния между ними .
Коэффициент пропорциональности в законе Кулона зависит от выбора системы единиц.
В системе СИ:
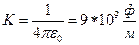, где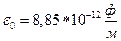 
.
В векторной форме закон Кулона можно записать:
Электрическая сила (сила Кулона) является центральной силой и действует вдоль прямой, соединяющей точечные заряды.
Сила взаимодействия между одноименным зарядами считается положительной,
.
Сила взаимодействия между разноименными зарядами считается отрицательной,
Экспериментально установлено, что наличие диэлектрической среды существенно влияет на величину силы Кулона.
Физическая величина, показывающая во сколько раз сила взаимодействия между точечными зарядами в вакууме больше, чем сила взаимодействия между ними в среде, называется диэлектрической проницаемостью среды.
И тогда закон Кулона в любой среде можно записать:
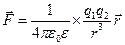
Электростатическое взаимодействие является взаимодействием на расстоянии и осуществляется посредством электростатического поля.
Электростатическое поле материально и оно является неотъемлемым свойством электрического заряда.
Электростатическое поле проявляется по наличию силового воздействия на пробный электрический заряд в него внесённый.
I Напряжённость электростатического поля
|
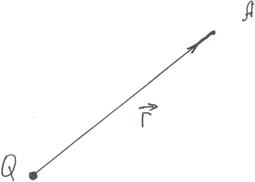
| Рис.1 |
Пусть электростатическое поле создаётся некоторым зарядом Q. Поместим в точку А на некотором расстоянии 
от этого заряда пробный заряд 
. Заряды Q и будут взаимодействовать с силой 
, величина, которой определяется законом Кулона.
Если в ту же точку поместить заряд 
, то сила взаимодействия будет равна 
и т.д. Из закона Кулона следует, что отношение силы к величине заряда, на который действует поле, для этой точки А будет всегда постоянным.
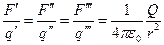= const
Напряженностью электростатического поля в данной точке называется векторная физическая величина, показывающая с какой силой действует электростатическое поле на единичный точечный положительный заряд, помещённый в данную точку поля.
За направление вектора напряженности электростатического поля принимается направление силы, действующей на положительный пробный заряд.
Единицей напряженности в системе СИ является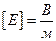 
Напряженность поля точечного заряда определяется выражением:
Если поле образовано несколькими зарядами, то напряженность результирующего поля определяется по принципу суперпозиции, т.е.
Напряженность поля, образованного несколькими зарядами, равна геометрической сумме напряженностей полей, созданных каждым зарядом в отдельности.
|
| Рис.2 |
Для графического изображения электростатического поля используются силовые линии.
Силовая линия- это воображаемая линия, касательная к каждой точке которой совпадает с направлением вектора напряженности этого поля.
Густота силовых линий выбирается так, чтобы через единичную поверхность, перпендикулярную силовым линиям, проходило количество силовых линий численно равное величине напряженности электростатического поля.
II. Поток вектора напряженности электростатического поля.
Пусть в некоторой точке пространства существует заряд q , создающий поле. На некотором расстоянии r от этого заряда проведём поверхность S , при условии, что r перпендикулярно S.
|
| Рис.3 |
Разобьём всю поверхность S на элементарные участки dS, площадь которых равна единице. Через каждый элемент поверхности dS проходит число силовых линий равное модулю вектора напряженности 
. Очевидно, через всю поверхность S пройдёт количество силовых линий равное:
.
Если же S и r не взаимно перпендикулярны, то через площадку dS пройдёт 
силовых линий. 
- проекция вектора напряжённости на внешнюю нормаль к поверхности S.
Общее число силовых линий через поверхность S в этом случае будет равно:
.
|
| Рис.4 |
В электродинамике величина, определяемая выражением:
называется потоком вектора напряжённости электростатического поля. 
является скалярной величиной и численно равен числу силовых линий, пересекающих поверхность S.
Силовые линии, идущие в направлении внешней нормали, считаются положительными.
Силовые линии, идущие в обратном направлении будут отрицательными.
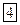1. Теорема Гаусса
Пусть некоторый точечный заряд q создаёт электростатическое поле, напряженность которого в любой точке пространства, равна:
.
Окружим заряд q воображаемой сферической поверхностью, площадь которой равна:
S= 
.
Найдем поток вектора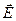 
через эту поверхность.
По определению он будет равен числу силовых линий, пересекающих эту поверхность:
.
В свою очередь 
.
Получим:
.
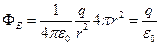Если поверхность, окружающая точечный заряд будет не сферическая, то результат будет тот же самый.
Знак потока вектора напряженности совпадает со знаком заряда, создающего поле.
Теорема Гаусса
Пусть внутри некоторой замкнутой поверхности произвольной формы находится несколько точечных электрических зарядов 
По определению
.
Исходя из принципа суперпозиции полей, результирующая напряженность будет равна:
И общая их проекция на внешнюю нормаль тоже будет равна:
Тогда
Учитывая соотношение 
, получим, что 
Теорема Гаусса.
Поток вектора напряжённости электростатического поля через замкнутую поверхность равен алгебраической сумме зарядов, заключённых внутри этой поверхности, делённой на электрическую постоянную.
Если же заряды внутри поверхности не точечные, а распределены по объёму с некоторой плотностью 
, то математическая запись теоремы Гаусса будет иметь вид:
Примеры расчёта напряжённости поля с помощью теоремы Гаусса.
1. Рассмотрим бесконечную плоскость, равномерно заряженную с поверхностной плотностью 
.
|
| Рис.5 |
Выделим на этой плоскости элемент поверхности 
, на котором построим цилиндр, образующие которого направлены параллельно вектору напряженности 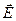. Поток вектора напряженности электростатического поля 
через боковую поверхность цилиндра равен нулю, так как силовые линии поля эту поверхность не пересекают. Поток вектора напряжённости через основания цилиндра равен:
.
По теореме Гаусса 
, получим 
.
2.В случае, если электростатическое поле создано двумя разноименно заряженными плоскостями, то напряженность поля между ними будет равна 
.
3. Определим напряженность поля заряженной сферы, радиус которой равен 
.
|
| Рис.6 |
Пусть поверхностная плотность заряда на сфере, тогда общий заряд на ней равен 
. Окружим сферу воображаемой поверхностью радиуса 
. Тогда поток напряженности через эту воображаемую поверхность по теореме Гаусса будет равен:
=. 
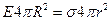
а) Работа сил электростатического поля.
|
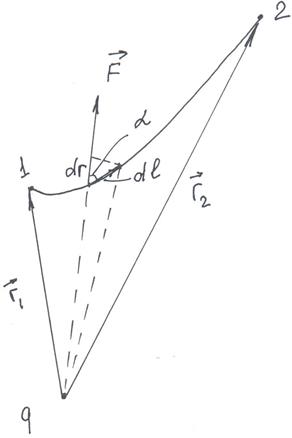
| Рис.7 |
Пусть поле создано точечным зарядом 
. В поле этого заряда из точки 1 в точку 2 перемещается заряд 
. 
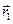и 
- радиус-векторы, определяющие положения точек 1 и 2. Будем считать, что заряд 
находится в начале системы отсчета. Определим работу по перемещению заряда в поле заряда из точки 1 в точку 2.
В любой момент времени положение определяется радиус-вектором . Разобьём всю траекторию движения заряда на элементарные отрезки 
. Тогда элементарная работа на отрезке 
будет равна:
где F- сила электростатического взаимодействия между зарядами и ,
- угол между векторами 
и .
По закону Кулона 
.
Из чертежа (Рис.7) видно, что приращение вектора при перемещении заряда вдоль элемента равно 
. Тогда элементарная работа будет равна
Полную работу получим, просуммировав все элементарные работы:
Изменив форму траектории движения заряда , проводя аналогичные рассуждения, получим тот же результат.
Следовательно:
Работа по перемещению заряда в электростатическом поле не зависит от формы пути, а определяется положением начальной и конечной точек траектории.
На основании этого можно сделать выводы:
1. Работа сил электростатического поля по замкнутому контуру всегда будет равна нулю.
2. Электростатическое поле является потенциальным, а электростатические силы – консервативными.
б) Теорема о циркуляции вектора напряженности электростатического поля.
Будем перемещать заряд 
по некоторому контуру длиной 
. Запишем элементарную работу на бесконечно малом отрезке этого контура:
По определению 
, следовательно 
.
Тогда элементарную работу можно записать 
, где 
модуль напряженности электростатического поля, а - угол между направлениями векторов 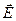и .
|
| Рис. 8 |
Из построения видно, что 
= 
, где 
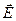проекция вектора на направление . Получили, что элементарная работа равна: вектора 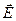на направление равна:
Полная работа по перемещению заряда по контуру , соединяющему точки 1 и 2, будет равна
Если заряд перемещают по замкнутому контуру, то полная работа должна быть равна нулю, следовательно,
.
Так как , значит
Выражение, стоящее в левой части, полученного соотношения называется циркуляцией вектора напряженности по замкнутому контуру.
Таким образом, можно считать доказанным, что:
Циркуляция вектора напряженности электростатического поля по замкнутому контуру равна нулю.
а) потенциал электростатического поля
Пусть в некотором пространстве сосредоточено электростатическое поле, созданное уединённым точечным зарядом .
Перенесем из бесконечности в произвольную точку А этого пространства пробный заряд .
Его потенциальная энергия, обусловленная взаимодействием поля и заряда, будет равна 
.
Если в ту же точку пространства поместить заряд , то его потенциальная энергия будет равна 
, поместим заряд - 
.
Так как изменение потенциальной энергии равно работе консервативных сил, взятой с обратным знаком, то при перемещении пробного заряда из бесконечности в данную точку поля,
= 
;
= 
и так далее.
Очевидно, что отношение 
Назовем потенциалом электростатического поля скалярную физическую величину, численно равную потенциальной энергии, которой обладает единичный положительный, точечный заряд, помещенный в данную точку поля.
Если поле создано точечным зарядом , то потенциал такого поля в каждой его точке равен:
Исходя из того, что работа есть мера изменения энергии, то при перемещении заряда из точки 1 в точку 2, она будет равна:
- называется разностью потенциалов, и она равна работе, которую совершает электростатическое поле при перемещении единичного положительного, точечного заряда из одной точки поля в другую.
б) Связь между напряженностью и потенциалом.
Итак, каждую точку электростатического поля можно характеризовать своими значениями напряженности и потенциала. Найдём математическую связь между ними.
Эту же работу можно определить, как убыль потенциальной энергии, т.е.
Из определения потенциала следует, что:
.
Приравняв выражения, определяющие работу, получим:
.
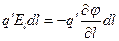Следовательно 
.
Если перейти к декартовой системе координат, то
; 
; 
Поскольку 
,
То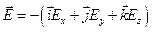 
.
Выражение, стоящее в скобках, называется градиентом и обозначается оператором 
.
Следовательно
Решая обратную задачу, получим: 
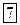Пусть поле создается системой точечных зарядов 
.
|
| Рис.9 |
Определим потенциал этого поля в точке 1. 
радиус-векторы, определяющие положение точки 1 относительно каждого из зарядов.
Работа, которую нужно совершить при перемещении заряда из точки 1 в точку 2, будет равна сумме работ против сил взаимодействия с каждым зарядом, создающим поле.
Ранее мы получили, что 
.
Следовательно,
.
Поскольку 
, получим 
.
Т.е. потенциал поля, созданного системой зарядов, равен алгебраической сумме потенциалов полей, создаваемых каждым зарядом в отдельности.
ЛЕКЦИЯ 2