Главная | Обратная связь

Электрическое поле в диэлектрике.

 

1. Полярные и неполярные молекулы. Вектор поляризации.

2. Характеристики поля диполя.

3. Электрический диполь в электростатическом поле.

4. Электрическое смещение (электростатическая индукция).

5. Сегнетоэлектрики и пьезоэлектрический эффект.

 

В диэлектриках нет свободных носителей заряда, они построены либо из нейтральных молекул, либо из заряженных ионов разных знаков, закрепленных в определенных положениях равновесия.

Под действием электростатического поля заряды в диэлектрике лишь смещаются из одного положения равновесия в другое.

Молекула диэлектрика называется полярной, если в отсутствие внешнего электростатического поля центры тяжести положительных и отрицательных зарядов не совпадают.

В противном случае молекула считается неполярной.

Во внешнем электростатическом поле любая молекула диэлектрика становится полярной, так как происходит смещение зарядов и деформация самой молекулы.

Чтобы определить степень воздействия электрического поля на молекулу, необходимо ввести количественную характеристику распределения зарядов в нейтральной молекуле.

Такой характеристикой является вектор электрического момента молекулы, определяемый соотношением:

Поскольку, в целом молекула электронейтральна, то и вектор электрического момента однозначно определяется только распределением заряда и не зависит от выбора системы координат.

В случае если молекула может быть представлена в виде двух равных разноимённых зарядов, то электрический момент равен:

, где q- величина заряда, взятого по модулю;

.

В отсутствие внешнего поля электрический момент неполярной молекулы равен нулю.

У неполярной молекулы электрический момент возникает только во внешнем поле и его величина пропорциональна напряженности внешнего поля.

Внешнее поле стремится сориентировать электрический момент вдоль своих силовых линий.

Таким образом, во внешнем электростатическом поле полярные и неполярные молекулы ведут себя как электрические диполи.

, где электрическая постоянная,

 

напряженность внешнего поля,

коэффициент поляризуемости молекулы.

Ориентация молекул диэлектрика во внешнем поле (поляризация диэлектрика) приводит к появлению результирующего электрического момента у всего диэлектрика.

 

Вектором поляризации называется физическая величина, равная векторной сумме электрических моментов молекул в единице объёма диэлектрика.

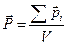
Можно записать:

,

 

где n-концентрация молекул диэлектрика,

- диэлектрическая восприимчивость диэлектрика.

 

 

а) Поскольку диполь является, по сути, системой из двух разноименных зарядов, то потенциал, создаваемый этой системой зарядов в некоторой точке А, можно записать:

Рис.10

где и -радиус-векторы, определяющие положения положительных и отрицательных зарядов относительно точки А. Учитывая, что 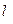- расстояние между зарядами, много меньше любого из r, получим:

Из построения следует, что

где - единичный вектор, направленный по r.

В результате, поскольку

получим:

= .

Для точечного диполя 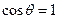, поэтому

б) Результирующая напряженность, создаваемая диполем в точке А, является векторной суммой напряженностей полей положительного и отрицательного зарядов.

 

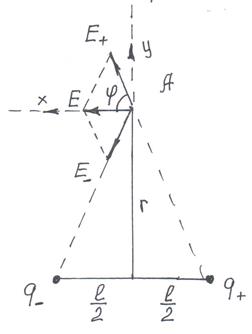
Рис.11

Сумма проекций напряженностей полей каждого из зарядов на ось OY будет равна нулю:

, проекции напряженностей на ось OX равны между собой и равны

.

Проводя несложные преобразования, получим:

Так как , то для точечного диполя

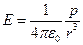
1. Диполь в однородном электрическом поле.

Однородным электрическим полем будем называть поле, напряженность 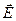которого в любой его точке остается постоянной по величине и направлению.

 

Рассмотрим поведение жесткого диполя во внешнем однородном электрическом поле.

Пусть вектор напряженности 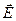составляет с электрическим моментом диполя 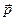угол .

Очевидно, на такой диполь будет действовать пара сил и ,которые равны по величине и противоположны по направлению.

Рис.12

Эта пара сил создаст вращательный момент равный:

т.к. , то

,

Учитывая, что , получим:

,

 

Во внешнем однородном электрическом поле на электрический диполь действует вращательный момент, под действием которого диполь стремится развернуться вдоль силовых линий внешнего поля.

 

Определим работу, которую необходимо совершить для поворота диполя в однородном электрическом поле на угол .

Элементарная работа по повороту диполя на угол 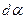равна:

 

.

Эта работа идет на увеличение потенциальной энергии диполя во внешнем электрическом поле:

.

 

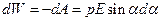Проинтегрировав по углу, получим, что энергия диполя равна:

 

.

 

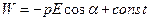Считая, что вне поля потенциальная энергия диполя равна нулю, константу интегрирования будем считать равной нулю.

 

2. Диполь в неоднородном электростатическом поле.

Рассмотрим теперь поведение диполя в неоднородном электрическом поле. Для простоты рассмотрим плоскую задачу, т.е. будем считать, что поле имеет осевую симметрию относительно оси ОХ.

Рис.13

Поскольку заряды и в этом случае, находятся в точках поля, имеющих разную напряженность, силы и будут иметь разную величину. Так как размер диполя мал, можно продолжать считать эти силы коллинеарными. Обозначим расстояние, на которое смещены заряды и по оси ОХ относительно друг друга через .

.

Напряженность поля на этом участке изменится на величину .

.

Проекция результирующей силы, действующей на диполь, на ось ОХ будет равна:

.

Если , то сила, действующая на диполь будет положительной и он будет втягиваться в область более сильного поля. При поле будет выталкивать диполь и сила считается отрицательной.

 

Таким образом, на диполь, находящийся в неоднородном электрическом поле, будут действовать одновременно вращательный момент и дополнительная сила, стремящаяся переместить его вдоль силовых линий внешнего поля.

Пусть диэлектрическая пластина находится во внешнем электрическом поле, напряженность которого перпендикулярна ее поверхности. Ориентация электрических диполей в пластине приводит к появлению на ее поверхности наведенного заряда .

Рис.14

 

Дипольный момент пластины будет равен: , где - поверхностная плотность наведенных зарядов; S- площадь пластины, - ее толщина. По определению вектор поляризации равен:

(*)

В случае, если вектор поляризации 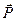составляет с нормалью к поверхности угол ,

Рис.15

то , где - проекция вектора поляризации на внешнюю нормаль к поверхности.

 

Соотношение (*) дает не только величину, но и знак поверхностного связанного заряда.

Если , то >0 и тоже положительная величина.

Если , то <0 и - отрицательная величина.

 

Электрическое воздействие поля на диэлектрик (поляризация) определяется суммарным электрическим полем, созданным свободными и связанными (наведенными) зарядами.

,

Где 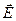- напряженность результирующего поля;

- напряженность поля свободных зарядов;

- напряженность поля связанных зарядов.

По теореме Гаусса поток вектора напряженности результирующего поля можно записать:

 

.

Получается, что результирующая напряженность 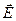связана с величиной наведенных зарядов, которая в свою очередь определяется той же напряженностью .

 

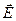Можно доказать, что поток вектора поляризации равен:

.

 

Подставив это выражение в теорему Гаусса, получим:

 

 

Или

 

Величина, стоящая в скобке называется вектором электрического смещения или электростатической индукцией и обозначается .

Теорему гаусса для вектора электрического смещения можно записать:

 

Поток вектора электрического смещения (электростатической индукции) через замкнутую поверхность равен сумме свободных зарядов, заключенных внутри этой поверхности.

В вакууме нет связанных зарядов, поэтому вектор поляризаци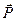и = 0 и

электростатическая индукция будет связана с напряженностью электростатического поля 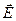соотношением:

.

 

В других диэлектриках 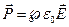, следовательно, ,

где - диэлектрическая проницаемость среды.

Полученное соотношение справедливо только для изотропных диэлектриков, т.к. только в этом случае вектора 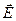и параллельны друг другу.

 

ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ.

 

1. Распределение избыточных зарядов на проводнике.

2. Проводники во внешнем электрическом поле.

3. Электроемкость. Конденсаторы.

 

Сообщим некоторому проводнику избыточные заряды . Процесс распределения заряда по проводнику будет продолжаться до тех пор пока не установится устойчивое равновесие. Определим условия, при которых это равновесие возможно.

 

- Во первых, и это очевидно, что напряженность результирующего поля внутри проводника должна быть тождественно равна нулю. ( ). Иначе на заряды будет действовать отличная от нуля сила, которая заставит их перемещаться по проводнику.

Учитывая, что , то при нулевой напряженности потенциал 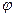электрического поля внутри проводника будет равен const. Это означает, что поверхность проводника является эквипотенциальной поверхностью.

 

- Во вторых, вектор напряженности электрического поля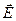

в каждой точке поверхности проводника должен быть

направлен по нормали к поверхности проводника ,

иначе опять результирующая сила, действующая на заряд,

не будет равна нулю.

 

Запишем теорему Гаусса для вектора :

 

Поскольку напряженность поле внутри проводника равна нулю, то , следовательно, .

Вывод: все избыточные заряды располагаются на поверхности проводника. Внутри проводника избыточных зарядов нет.

Поместим незаряженный проводник во внешнее электрическое поле

Рис.16

напряженностью .

Под действием этого поля свободные заряды

в проводнике переместятся так, что на одной

грани его возникнет избыток отрицательных

зарядов, а на другой – положительных.

Возникшее собственное поле этих зарядов

будет направлено противоположно внешнему, и

будет ослаблять его действие.

В результате перераспределение зарядов будет

происходить до тех пор пока собственное

внутреннее поле не скомпенсирует внешнее.

 

Вывод: в результате перераспределения свободные заряды также расположатся на поверхности проводника.

 

Таким образом, и индуцированные (наведенные) и избыточные заряды располагаются на поверхности проводника.

Это приводит к тому, что, если внутри проводника есть полость, то электрического поля в ней не будет. На этом основана, так называемая электростатическая защита.

 

 

Сообщим изолированному проводнику некоторый заряд и измерим потенциал электростатического поля, создаваемого этим зарядом, в точке А.

 

Заряд создаст в точке А поле с потенциалом .

 

И так далее .

 

Т.е., потенциал поля заряженного уединенного проводника будет пропорционален величине заряда на проводнике.

 

.

 

С – электроемкость проводника, физическая величина численно равная величине заряда, сообщение которого проводнику увеличивает потенциал этого проводника в некоторой точке на единицу потенциала.

( )

 

В системе СИ единицей электроемкости является фарад .

Один фарад – это электроемкость такого проводника, у которого сообщение ему заряда в один Кулон вызывает повышение потенциала на один вольт.

 

 

Вычислим электроемкость заряженного шара (сферы) радиуса R.

 

Будем считать шар уединенным, т.е. .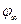

Используя теорему о циркуляции вектора напряженности электростатического поля, можно записать:

.

Учитывая определение электроемкости и то, что на потенциал равен нулю, получим:

.

Если шар находится в диэлектрической среде с проницаемостью , электроемкость будет равна: .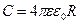

Легко подсчитать, что электроемкостью в один фарад в вакууме обладает уединенный шар, радиус которого примерно равен 9 м, что в 1500 раз больше радиуса Земли.

Если проводник не будет уединенным, т.е. вблизи него находятся другие проводники, пусть даже не заряженные, то сообщение ему заряда вызовет перераспределение зарядов на соседних проводниках, что в свою очередь повлияет на распределение зарядов на самом проводнике. При достижении равновесия заряды в системе проводников расположатся так, чтобы поле внутри каждого проводника было равно нулю.

В результате , потенциал заряженного проводника окажется равным сумме потенциалов полей собственных перераспределившихся зарядов и зарядов индуцированных на других проводниках, что приведет к увеличению электроемкости этого проводника.

 

 

Это явление используется при создании устройств, называемых конденсаторами, основное назначение которых накапливать электрический заряд.

Любой конденсатор состоит из двух или более обкладок (металлических проводников), разделенных между собой слоем диэлектрика.

Конденсаторы различаются по форме обкладок: плоские, цилиндрические, сферические и по типу диэлектрика: воздушные, масляные, керамические, бумажные и др.

Основной характеристикой конденсатора является электроемкость:

,

где - разность потенциалов между обкладками конденсатора.

 

Электроемкость плоского конденсатора равна:

,

где - диэлектрическая проницаемость диэлектрика между обкладками конденсатора,

- площадь его обкладок, - расстояние между обкладками.

Емкость сферического конденсатора равна:

,

где R и r – радиусы внешней и внутренней сфер, соответственно.

Емкость цилиндрического конденсатора зависит от его длины L и радиусов его внешнего

и внутреннего цилиндров (R, r):

 

.

 

В электрической цепи конденсаторы можно соединять в системы:

- при последовательном соединении конденсаторов складываются величины обратные электроемкости

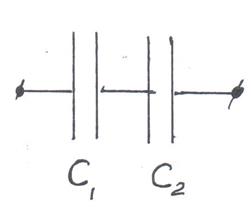
Рис.17

 

,

 

 

-при параллельном соединении общая электроемкость равна:

 

Рис.18

 

Сила притяжения между обкладками конденсатора равна:

 

Где общее напряжение, поданное на конденсатор,

- поверхностная плотность зарядов на обкладках конденсатора.

 

ЛЕКЦИЯ 4.

 

ЭНЕРГИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ.

 

 

1. Энергия системы зарядов.

2 Энергия заряженного проводника и конденсатора.

3. Энергия электростатического поля.

4. Теорема ИрнШоу.

 

 

Определим потенциальную энергию (энергию взаимодействия) системы из двух точечных зарядов и .Будем считать, что в начальный момент заряды находятся на бесконечно большом расстоянии друг от друга и не взаимодействуют между собой. Следовательно, их начальная потенциальная энергия равна нулю.

Рис.19

 

радиус вектор, соединяющий заряды.

 

Начнем сближать эти заряды. При этом будет совершаться работа, которая идет на увеличение потенциальной энергии всей системы. Это утверждение двузначно.

Можно закрепить заряд и перемещать заряд в поле первого заряда, а можно наоборот. Из консервативности природы сил электростатического поля следует, что работа в обоих случаях будет одинакова, т.е. .

По определению эта работа равна:

.

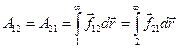В тоже время работа есть изменение потенциальной энергии:

 

.

Так как при , то

.

С другой стороны:

,

 

где - потенциал поля, создаваемый зарядом в точке, где находится заряд ,

потенциал поля, создаваемый зарядом в точке, где находится заряд .

 

Поскольку задача симметричная, то можно записать:

.

 

Если же система состоит из n зарядов, то, использую тот же прием, получим:

 

,

 

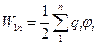Где 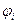- потенциал поля, созданного всеми зарядами кроме i- того, в точке, где находится заряд .

 

При выводе данного соотношения мы пользовались представлениями о точечных зарядах, чтобы освободиться от этих ограничений, представим всю систему зарядов, как совокупность объемных и поверхностных зарядов, и тогда:

 

,

где потенциал поля всех объемных и поверхностных зарядов в данной точке.

 

 

1) Энергия заряженного проводника.

Рассчитаем работу, которую надо совершить, чтобы перенести некоторое количество заряда из бесконечности на данный проводник.

В начальный момент потенциальная энергия незаряженного проводника равна нулю. При переносе из бесконечности на данный проводник заряда работа сил электростатического поля равна нулю. При переносе новой порции заряда эта работа уже отлична от нуля, т. к теперь проводник заряжен.

.

Выразим потенциал на проводнике через заряд и его электроемкость:

.

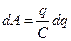Поскольку , то .

.

Так как незаряженный проводник не имеет потенциальной энергии, то ,

и следовательно, .

Учитывая соотношение между зарядом, электроемкостью и потенциалом, получим:

,

 

где 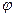- потенциал проводника, имеющего заряд .

2) Энергия заряженного конденсатора.

Появление заряда на обкладках конденсатора представим как перемещение порции заряда с одной пластины на другую.

В этом случае работа по перемещению заряда будет равна:

 

,

 

где - разность потенциалов на обкладках конденсатора.

 

.

 

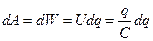Проведя интегрирование, получим:

.

 

Энергия незаряженного конденсатора равна нулю ,

 

где C – емкость конденсатора.

 

Энергию плоского заряженного конденсатора выразим через величины, характеризующие электростатическое поле в зазоре между обкладками конденсатора.

Пусть конденсатор заряжен до разности потенциалов , учитывая, что конденсатор плоский, получим:

.

 

Умножим и разделим это выражение на :

 

.

 

Так как поле в плоском конденсаторе однородное и объем конденсатора равен

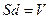, получим:

Введем новую физическую величину, которую назовем объемной плотностью энергии:

 

 

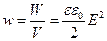
Получили, что энергия электростатического поля пропорциональна квадрату напряженности поля.

 

Где же сосредоточена эта энергия и что является носителем – поле или заряд.

В пределах электростатики, которая изучает неподвижные заряды, ответить на этот вопрос невозможно, поскольку заряд и поле неразрывно связаны между собой и разделить их нельзя.

В электродинамике, которая изучает изменяющиеся электрические и магнитные поля, доказано, что электромагнитное поле способно существовать и распространяться в пространстве независимо от возбудивших его зарядов в виде электромагнитной волны, которая и переносит энергию.

Отсюда вывод, что носителем энергии все-таки является поле.

 

Поскольку между обкладками конденсатора находится диэлектрик, то энергию электростатического поля справедливей было выразить через вектор электростатической индукции .

Считая диэлектрик между обкладками изотропным, , получим:

.

 

Путем несложных преобразований, выразим объемную плотность энергии электромагнитного поля с учетом вектора поляризации .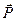

 

.

 

определяет объемную плотность энергии электростатического поля в вакууме,

 

численно равно энергии, которая затрачивается на работу по поляризации диэлектрика.

 

 

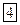Для построения теории строения материи чрезвычайно важно установление возможности существования устойчивых конфигураций электрических зарядов. Поскольку все атомы состоят из заряженных частиц (электроны, протоны), то необходимо определить условия, при которых эти заряды будут находиться в положении устойчивого равновесия.

Известно, что в положении устойчивого равновесия любая система должна обладать минимумом потенциальной энергии. В данном случае минимальной должна быть электрическая энергия, которая для системы зарядов определяется выражением:

 

,

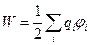где -потенциал поля, созданного всеми зарядами, кроме ого, в точке поля, где находится ый заряд.

 

 

.

 

 

Функция будет иметь минимальное значение, если ее первые производные по всем координатам равны нулю, а вторые производные положительны.

Ирн Шоу математически показал, что выполнение этих двух условий одновременно для статических зарядов невозможно. Им же была сформулирована теорема, носящая его имя.

 

Устойчивая конфигурация неподвижных электрических зарядов невозможна.

 

Атом устойчив, так как он является динамической системой.

 

 

ПОСТОЯННЫЙ ТОК.