 |
|
ПИТОМА ПОТЕНЦІЙНА ЕНЕРГІЯ ПРУЖНОЇ ДЕФОРМАЦІЇ ПРИ СКЛАДНОМУ НАПРУЖЕНОМУ СТАНІ
В §13 ми встановили, що питома потенційна енергія пружної деформації при розтязі (стискові), тобто при лінійному напруженому стані виражається формулою (10' ) :
U =  ,
,
або враховуючи, що Е =  маємо :
маємо :
U =  . (32)
. (32)
Тепер перейдемо до визначення кількості питомої потенційної енергії для тіла, що знаходиться в умовах складного (об’ємного та плоского) напруженого стану. Користуючись принципом незалежності дії сил і вважаючи, що головні напруги зростають поступово, знайдемо потенційну енергію, як суму енергій, що накопичуються в одиниці об’єму матеріалу під дією кожної із головних напруг σ1, σ2 і σ3 за формулою ( 32)
U =  +
+  +
+ 
де ε1 ,ε2 і ε3 - відносні деформації, що знаходяться за формулами (28).
Тоді
U= 
або, розкривши дужки:
U =  (33)
(33)
Таким чином, повна питома потенційна енергія деформації, що накопичується в одиниці об’єму матеріалу (кубик зі сторонами, що дорівнюють одиниці довжини), може бути знайдена за формулою (33). Ця енергія, може розглядатися як енергія, що складається із двох частин:
1) енергії Uv, що накопичується за рахунок зміни об’єму V даного кубика (тобто, однакової зміни всіх його розмірів без зміни кубічної форми) і
2) енергії Uф, пов’язаної зі зміною форми кубика (тобто енергії, що витрачається на перетворення кубика в паралелепіпед).
Такий поділ потенційної енергії на дві частини є зручним при подальшому вивченні питання про міцність матеріалу при об’ємному напруженому стані.
Знайдемо величину обох складових питомої потенційної енергії. Вище було показано (§22), що при однаковій деформації ребер кубика, тобто тільки при зміні об’єму, відносна деформація кожного ребра дорівнює (формула 32):
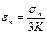 ,
,
де  , а об’ємний модуль пружності К =
, а об’ємний модуль пружності К =  .
.
Тоді енергія зміни об’єму буде :
Uv = 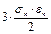 =
= 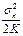 =
= 
або:
Uv = 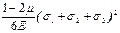 (34)
(34)
Потенційна енергія, що пов’язана із зміною форми виділеного елемента матеріалу, знаходиться як різниця:
Uф = U – Uv ,
або:
Uф =  –
– 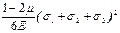
Зробивши відповідні розрахунки, маємо :
Uф =  (35)
(35)
При простому осьовому розтязі, коли 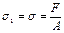 ,
,  і
і  питома потенційна енергія, що пов’язана із зміною об’єму елементарного кубика
питома потенційна енергія, що пов’язана із зміною об’єму елементарного кубика
Uv =  , (36)
, (36)
а потенційна енергія зміни форми
Uф = 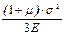 . (37)
. (37)
Зрозуміло, що їх сума дає повну питому енергію розтягу :
U = Uv + Uф =  +
+ 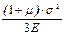 =
=
 =
= 
§ 25 . ПОНЯТТЯ ПРО ТЕОРІЇ МІЦНОСТІ
В §15 розглядалося питання про міцність матеріалу при лінійному напруженому стані: при осьовому розтязі, коли головні напруги мають значення:
 , σ2 = 0, σ3 = 0
, σ2 = 0, σ3 = 0
або при осьовому стискові коротких стержнів, коли
σ1 = 0, σ2 = 0, 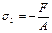
В цьому випадку перевірка міцності проводиться за умовою
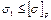 або
або 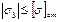
Буквою [σ] позначається допустима напруга при розтязі або стискові. Для більшості пластичних матеріалів ці значення однакові, для крихких - різні.
В §14 вказано, що допустима напруга визначається з таким розрахунком, щоб був забезпечений відомий запас міцності у порівнянні із небезпечним (граничним) станом :
 ,
,
де σгр – напруга, що характеризує небезпечний (граничний) стан. При статичному навантаженні для пластичного матеріалу такий стан характеризується появою великих залишкових деформацій, а для крихкого – появою тріщин, руйнуванням матеріалу. Тоді у першому випадку σгр = σт, а у другому – σгр = σв.
Для лінійного напруженого стану ці величини отримуються безпосередньо із лабораторних випробувань на розтяг або стиск. Цей дослід легко здійснити в лабораторії і безпосередньо знайти величину границі текучості і міцності.
Розглянемо тепер, як зробити перевірку міцності в тих випадках, коли дві або три головні напруги σ1, σ2, σ3 не дорівнюють нулю (рис.28).
В цьому випадку початок небезпечного стану матеріалу може бути викликаний різними числовими значеннями головних напруг σ1, σ2, σ3 залежно від величини відношення їх однієї до другої. Кожній комбінації цих відношень будуть відповідати певні небезпечні величини головних напруг, при яких настає небезпечний стан матеріалу (поява великих залишкових деформацій або тріщин).
Таким чином, для знаходження цих небезпечних значень напруг σ1, σ2, σ3 в лабораторії потрібно проводити випробування длярізних співвідношень 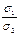 ,
,  . Практично здійснити такі випробування неможливо через труднощі їх постановки і великої кількості випробувань.
. Практично здійснити такі випробування неможливо через труднощі їх постановки і великої кількості випробувань.
Тому необхідно знайти спосіб скласти умову міцності для складного напруженого стану, користуючись величинами σт і σв, отриманих при дослідах для лінійногонапруженого стану. Іншими словами виникла потреба створити теорію (гіпотезу), яка дозволила б замінити складний напружений стан еквівалентним йому лінійним напруженим станом.
Виявляється, що така заміна можлива, якщо прийняти якесь припущення про те, який фактор є вирішальним у появі небезпечного стану матеріалу, або, іншими словами, що є причиною появи текучості або руйнування матеріалу.
Таких факторів можна намітити декілька. Дійсно, навіть при простому розтязі стержня із пластичного матеріалу можна поставити питання : що є причиною текучості ?
Можна вважати, що текучість з’явиться тоді, коли найбільші нормальні напруги в стержні досягнуть границі текучості σт. Але можна вважати, що поява текучості настане тоді, коли найбільше видовження матеріалу досягне повного значення. Можна зробити і третє припущення, що поява великих залишкових деформацій пов’язана з тим, що дотичні напруги досягли певної величини.
Таким чином, ми можемо висловити ряд гіпотез, побудувати ряд так званих теорій міцності. Як ми побачимо далі, при простому розтязі або стискові, при лінійному напруженому стані результати перевірки міцності виявляються однаковими, яку б із гіпотез ми не прийняли. Це пояснюється тим, що в цьому випадку перевірка міцності спирається безпосередньо на досліди.
Зовсім інакше це буде при складному напруженому стані. Нижче буде показано, як змінюється умова міцності залежно від прийнятої теорії. Вибір тої чи іншої теорії остаточно визначається перевіркою її на досліді для випадку складного напруженого стану.
Перш ніж перейти до викладення теорій міцності, відмітимо, що небезпечний стан для різних матеріалів лежить на границі застосування закону Гука (з відомим, достатнім для практики, наближенням). Це дозволить при всіх подальших підрахунках, що відносяться до перевірки міцності, користуватися формулами, що виведені за умови застосування закону Гука.
Перша теорія міцності або теорія найбільших нормальних напруг.Ця теорія передбачає, що небезпечний стан матеріалу настає тоді, коли найбільша за абсолютною величиною нормальна напруга досягає небезпечного значення.
Таким чином, і в загальному випадку, коли всі три головні напруги σ1, σ2 і σ3 не дорівнюють нулю, при перевірці міцності потрібно враховувати тільки найбільшу напругу розтягу або стиску. Величина двох інших напруг як би не має ніякого значення. Фактично втрачається різниця між лінійним та складним напруженим станом.
Умова міцності для цієї теорії має вигляд :
σ1 ≤ [σ] або |σ3| ≤ [σ]ст
При перевірці вказаної теорії на дослідах, виявилася невідповідність її висновків з результатами випробувань на всесторонній стиск не тільки пластичних матеріалів, але і крихких. Наприклад, випробуваний таким чином бетонний кубик витримав набагато більші напруги, ніж при одноосному стискові, не виявивши при цьому ніяких ознак руйнування. Лише для випадку розтягу крихких матеріалів ця теорія відповідає дослідним даним. Так як ця теорія дає або більші, або менші розміри перерізів елементів конструкцій при складному напруженому стані, нею уникають користуватися.
Друга теорія міцності або теорія найбільших лінійних деформацій.Ця теорія передбачає, що міцність елемента, який знаходиться у складному напруженому стані, забезпечена, якщо найбільші відносні деформації не перевищують допустимої деформації для лінійного напруженого стану, тобто
 , (38)
, (38)
де 
Припустимо, що при плоскому напруженому стані небезпечним відносним видовженням буде ε1, тобто εмах = ε1, тоді
 (38´)
(38´)
Виразивши умову міцності (38´) через напругу і використавши формули (28), можна записати
 ,
,
або, скорочуючи на Е, отримаємо
 (39)
(39)
Якщо небезпечним відносним видовженням буде ε2, то умова міцності запишеться так :
 39')
39')
Для об’ємного напруженого стану замість формули (39) отримаємо
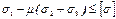 (39' )
(39' )
Як бачимо із формул ( 39 ) і ( 39 ′ ), з допустимою напругою
[σ] порівнюються не головні напруги σ1 або σ2, а їх комбінація σ1μσ2 або σ2 μσ1, яка називається еквівалентною напругою.
За допомогою еквівалентної напруги будь-який напружений стан можна звести до осьового розтягу або стиску, причому стає можливим не проводити обчислень лінійних деформацій, а виразити умову міцності через нормальні напруги. Позначивши еквівалентну напругу σекв, формулу (39'') можна представити у вигляді :
σекв = σ1 μ ( σ2 σ3 ) ≤ [σ ] (39 ''')
Таким чином, при перевірці міцності матеріалу за другою теорією потрібно визначити еквівалентну напругу за формулою (39''') і порівняти її з допустимою напругою.
Друга теорія міцності не підтверджується дослідами для пластичних матеріалів. Вона дає задовільні результати при випробуванні крихких матеріалів, але для деяких типів напруженого стану.
Третя теорія міцності або теорія найбільших дотичних напруг. Ця теорія передбачає, що міцність елемента, який знаходиться у складному напруженому стані, забезпечена, якщо найбільші дотичні напруги в його перерізах не перевищують допустимої дотичної напруги для лінійного напруженого стану елемента із того ж матеріалу:

Виразивши дотичну напругу через нормальну за формулами (23) і (27), умова міцності може бути представлена у вигляді:
 (40)
(40)
або
σекв = σ1 - σ3 ≤ [σ] (40′)
Як видно із формули ( 40 ) третя теорія враховує тільки дві головні напруги – найбільшу та найменшу . Недоліком цієї теорії є те, що вона не враховує проміжної головної напруги, яка теж впливає на міцність матеріалу.
Третя теорія міцності підтверджується результатами дослідів для пластичних матеріалів, міцність яких на розтяг та стиск однакова. Тому цю теорію інколи називають теорією пластичності. Для крихких матеріалів результати дослідів не відповідають третій теорії.
У зв′язку з недоліком старих теорій виникли нові ідеї відносно того, який фактор викликає небезпечний стан матеріалу.
Ряд авторів висловили припущення, що небезпечний стан матеріалу залежить не від величини деформацій або напруг окремо, а від сукупності тих і інших - від величини питомої потенційної енергії деформації. Ця величина виражається через всі три головні напруги.
Якщо зробити припущення, що причиною небезпечного стану є накопичення повної питомої потенційної енергії деформації, то міцність матеріалу буде забезпечена при умові, що U ≤ [U], де [U] – допустима кількість потенційної енергії, яка може бути отримана із формули (10') для повної енергії деформації при осьовому розтязі.
Ця теорія дослідами не підтвердилася і має тільки історичне значення. Але вона виявилася базою для створення нової енергетичної теорії міцності, яка досить добре узгоджується з дослідами.
Цю теорію, що називають четвертою теорією міцності, або теорією питомої потенційної енергії зміни форми, можна сформулювати так: міцність елемента, що знаходиться у складному напруженому стані, забезпечена, якщо найбільша питома потенційна енергія зміни форми не перевищує допустимого її значення для лінійно напруженого елемента із того ж матеріалу, тобто
Uф ≤ [Uф]
Тут Uф – потенційна енергія зміни форми для складного напруженого стану – визначається за формулою ( 35 ):
Uф = 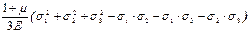
Величина допустимої потенційної енергії зміни форми для випадку простого розтягу дорівнює (37):
[Uф] =  ,
,
тоді умова міцності буде мати вигляд:
 (41)
(41)
Умову міцності (41) можна представити у іншому вигляді, інколи більш зручному для підрахунків :
 (42)
(42)
Умова міцності для плоского напруженого стану (при σ3 = 0 ) виразиться формулою :

 (42')
(42')
Відмітимо, що цю теорію, як і третю, можна вважати теорією міцності за умови, що за небезпечний стан матеріалу приймають його перехід в пластичний стан.
Теорія міцності Мора.Крім розглянутих вище теорій, були запропоновані і інші, із яких потрібно відмітити теорію О.Мора, за якою умова міцності може бути представлена у вигляді:
σекв = (σ1 n σ3) ≤ [σ]р (43)
де n – відношення граничних напруг при розтязі і стискові:
для крихких матеріалів
 ,
,
для крихко–пластичних матеріалів
 .
.
Для пластичних матеріалів n = 1 і умова міцності (43) приймає вигляд, аналогічний третій теорії. Тому теорію міцності Мора можна розглядати як узагальнення третьої теорії для крихких та крихко-пластичних матеріалів.
Як видно із формули (43), ця теорія також, як і третя, не враховує проміжної головної напруги σ2, що є її недоліком. Для крихких матеріалів теорія міцності Мора дає задовільні результати.
Приклад 15.Перевірити міцність матеріалу елемента (рис. 32) за третьою і четвертою теоріями міцності, якщо на нього діють головні напруги σ1 = 100 МПа і σ2 = 30 МПа. Допустима напруга [σ] = 160 МПа.
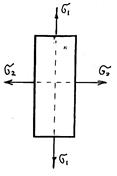
Рис. 32
Розв’язок.За третьою теорією міцності
σекв = (σ1 σ2) ≤ [σ] = 100 – 30 = 70 МПа < [σ] = 160 МПа
елемент задовольняє умову міцності.
За четвертою теорією міцності
 =
= = 88,88 МПа < 160МПа
= 88,88 МПа < 160МПа
елемент також задовольняє умову міцності.
Питання для самоконтролю
1. Які напруги виникають в похилих перерізах бруса при розтязі та стискові?
2.В яких перерізах виникають найбільші нормальні та дотичні напруги при розтязі та стискові?
3. Чому дорівнює сума нормальних напруг в двох взаємно перпендикулярних перерізах, що розтягуються?
4. В чому суть закону парності дотичних напруг?
5. Які напруги називаються головними?
6. Який напружений стан матеріалу називається лінійним, плоским, об'ємним?
7. Яка мета теорій міцності? В чому їх суть?
8. Які теорії придатні для розрахунку пластичних матеріалів, а які для крихких?