 |
|
Определитель второго порядка. Решение системы двух линейных уравнений с двумя переменными по формулам Крамера.
Определение. Определителем второго порядка называется число, которое записывается и вычисляется следующим образом:

Пусть дана система уравнений вида  (*)
(*)
Введем в рассмотрение следующие определители:
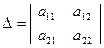 ;
; 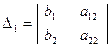 ;
; 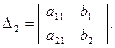
Теоретически возможны следующие три случая.
1. Если  , то система (*) имеет единственное решение, которое можно найти по формулам, которые называются формулами Крамера:
, то система (*) имеет единственное решение, которое можно найти по формулам, которые называются формулами Крамера:  ,
,  .
.
2. Если  , а
, а  (тогда и
(тогда и  ), то система (*) не имеет решений.
), то система (*) не имеет решений.
3. Если  и
и  (тогда и
(тогда и 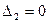 ), то система (*) имеет бесконечное множество решений (а именно, каждое решение одного уравнения системы является и решением другого ее уравнения).
), то система (*) имеет бесконечное множество решений (а именно, каждое решение одного уравнения системы является и решением другого ее уравнения).
Замечание. Определитель  называется главным определителем системы (*). Систему можно решать по формулам Крамера только при условии
называется главным определителем системы (*). Систему можно решать по формулам Крамера только при условии  . В противном случае нужно использовать другие методы, например метод Гаусса.
. В противном случае нужно использовать другие методы, например метод Гаусса.
Определитель третьего порядка. Решение системы трех линейных уравнений с тремя переменными по формулам Крамера
Определение. Определителем третьего порядка называется число, которое записывается и вычисляется следующим образом:
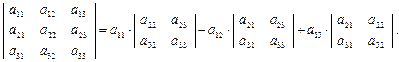
Пусть дана система уравнений вида  (*)
(*)
Введем в рассмотрение следующие определители:
 – главный определитель системы (*);
– главный определитель системы (*);
 ;
;  ;
;  .
.
При решении системы возможны следующие случаи.
1. Если  , то система (*) имеет единственное решение, которое можно найти по формулам, которые называются формулами Крамера:
, то система (*) имеет единственное решение, которое можно найти по формулам, которые называются формулами Крамера:  .
.
2. Если  , то решить систему (1) методом Крамера нельзя.
, то решить систему (1) методом Крамера нельзя.
Замечание 1. В случае  система может не иметь решений или иметь бесконечное множество решений. Для более детального исследования и нахождения общего системы решения можно использовать, например, метод Гаусса.
система может не иметь решений или иметь бесконечное множество решений. Для более детального исследования и нахождения общего системы решения можно использовать, например, метод Гаусса.
Решение системы трех линейных уравнений с тремя переменными
Методом Гаусса
Суть метода Гаусса рассмотрим на конкретном примере.
Пример. Решить систему уравнений:  (*)
(*)
Прямой ход. Данная система приводится к треугольному виду поэтапно методом алгебраического сложения.
На первом этапе исключим из второго и третьего уравнений системы  слагаемые, содержащие переменную
слагаемые, содержащие переменную  . Лучше использовать в обоих случаях одно и то же уравнение (мы возьмем первое).
. Лучше использовать в обоих случаях одно и то же уравнение (мы возьмем первое).

Получаем:

| 
|
Первое уравнение системы  перепишем без изменений, а второе и третье уравнения заменим полученными уравнениями.
перепишем без изменений, а второе и третье уравнения заменим полученными уравнениями.
Система  примет вид:
примет вид: 

На втором этапе исключим из третьего уравнения системы  слагаемое, содержащее переменную
слагаемое, содержащее переменную  . Используем для этого второе уравнение.
. Используем для этого второе уравнение.
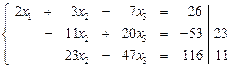
| Получаем: | 
|
Первые два уравнения системы  перепишем без изменения, а третье уравнение заменим полученным уравнением.
перепишем без изменения, а третье уравнение заменим полученным уравнением.
Получаем систему треугольного вида: 
Обратный ход. Последовательно находим неизвестные, начиная с третьего уравнения.
Из третьего уравнения системы находим значение переменной  :
: 

 .
.
Подставив найденное значение 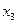 во второе уравнение системы, получаем
во второе уравнение системы, получаем 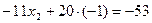 , откуда находим значение переменной
, откуда находим значение переменной  :
: 





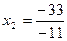

 .
.
Подставив найденные значения 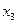 и
и  в первое уравнение системы, получаем
в первое уравнение системы, получаем  , откуда находим значение переменной
, откуда находим значение переменной  :
: 







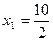

 .
.
Ответ: 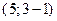 .
.
22. Решение линейного неравенства 
При решении неравенства  возможны следующие случаи:
возможны следующие случаи:
| Примеры |
1. Если  , то , то  . .
|   
|
2. Если  , то , то  . .
|   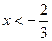
|
3. Если  , ,  , то , то 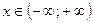 . .
|   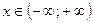
|
4. Если  , ,  , то неравенство
не имеет решений. , то неравенство
не имеет решений.
| Неравенства  и и  не имеют решений.
не имеют решений.
|
23. Решение линейного неравенства 
При решении неравенства  возможны следующие случаи:
возможны следующие случаи:
| Примеры |
1. Если  , то , то  . .
| 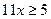  
|
2. Если  , то , то 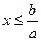 . .
| 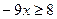  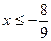
|
3. Если  , ,  , то неравенство
не имеет решений. , то неравенство
не имеет решений.
| Неравенство  не имеет решений.
не имеет решений.
|
4. Если  , ,  , то , то 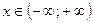 . .
|   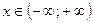
  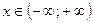
|
24. Решение систем линейных неравенств с одной переменной
Система неравенств – это два или большее количество неравенств, для которых ищут общие решения.
Решением системы неравенств называется общее решение всех неравенств, входящих в систему.
Теоретически возможных случаев даже для системы двух неравенств очень много, поэтому рассмотрим основные случаи для системы двух простейших неравенств.
 Пример 1. Решить систему неравенств:
Пример 1. Решить систему неравенств: 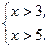
Изобразим решения неравенств графически.
Ответ:  .
.
 Пример 2. Решить систему неравенств:
Пример 2. Решить систему неравенств: 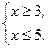
Изобразим решения неравенств графически.
Ответ:  .
.
 Пример 3.Решить систему неравенств:
Пример 3.Решить систему неравенств: 
Изобразим решения неравенств графически.
 Ответ:
Ответ:  .
.
Пример 4. Решить систему неравенств: 
Изобразим решения неравенств графически.
 Ответ: система не имеет решений.
Ответ: система не имеет решений.
25. Решение неполных квадратных уравнений 
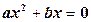 ,
,  ,
, 
Квадратным уравнением называется уравнение вида  , причем.
, причем.
Квадратное уравнение называется неполным, если хотя бы один из коэффициентов  или
или  равен нулю.
равен нулю.
Каждое из неполных уравнений можно решить по общей формуле. Но удобнее использовать частные методы.
Случай 1. Если  , то уравнение принимает вид
, то уравнение принимает вид  .
.
Левую его часть можно разложить на множители:  . Известно, что произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Получаем:
. Известно, что произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Получаем: 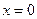 или
или  , откуда в силу условия
, откуда в силу условия  следует, что
следует, что  .
.
Вывод: уравнение  всегда имеет два действительных корня
всегда имеет два действительных корня  ,
,  .
.
Пример 1. Решить уравнение 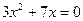 .
.
Решение: 

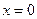 или
или 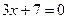

 ,
, 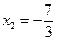 .
.
Случай 2. Если  , то уравнение принимает вид
, то уравнение принимает вид  .
.
Тогда  . Поскольку
. Поскольку  , то
, то  .
.
Если  , это уравнение не имеет действительных корней (так как
, это уравнение не имеет действительных корней (так как  ).
).
Если 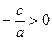 , то уравнение имеет два действительных корня
, то уравнение имеет два действительных корня  .
.
Пример 2. Решить уравнение 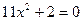 .
.
Решение: 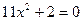

 . Так как
. Так как  ,
,  , то данное уравнение не имеет действительных корней.
, то данное уравнение не имеет действительных корней.
Пример 3. Решить уравнение  .
.
Решение: 



 .
.
Случай 3. Если  и
и  , то уравнение принимает вид
, то уравнение принимает вид  .
.
Так как  , то
, то  , или
, или 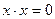 , поэтому уравнение имеет два равных корня
, поэтому уравнение имеет два равных корня  .
.
Пример 4. Решить уравнение 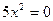 .
.
Решение: 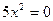



 .
.
26. Решение приведенного квадратного уравнения 
Приведенным квадратным уравнением называется квадратное уравнение  , старший коэффициент которого
, старший коэффициент которого  .
.
Чтобы найти его корни, выделим полный квадрат с переменной x. Получим:


 .
.
Число  называется дискриминантом приведенного квадратного уравнения. От знака дискриминанта зависит количество действительных корней уравнения.
называется дискриминантом приведенного квадратного уравнения. От знака дискриминанта зависит количество действительных корней уравнения.
Если  , то уравнение не имеет действительных корней, так как
, то уравнение не имеет действительных корней, так как  .
.
Если  , то
, то  ,
, 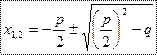 ,то естьданное уравнение имеет два действительных корня
,то естьданное уравнение имеет два действительных корня  и
и  .
.
Замечание. Формулу  особенно удобно использовать, если коэффициент p является четным числом.
особенно удобно использовать, если коэффициент p является четным числом.
Пример. Решить уравнение  .
.
Решение. Так как 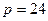 , то
, то  ,
,  , поэтому
, поэтому 





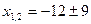 .
.
Тогда  ,
,  .
.
Ответ:  ,
, 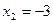 .
.
27. Формулы Виета для приведенного квадратного уравнения
В предыдущем параграфе показано, что уравнение  при условии
при условии  имеет два действительных корня и
имеет два действительных корня и  .
.
Тогда  ,
,
 .
.
Таким образом доказана теорема, которая называется теоремой Виета.
Теорема. Если  и
и  – корни приведенного квадратного уравнения
– корни приведенного квадратного уравнения  , то справедливы равенства
, то справедливы равенства  ,
, 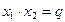 .
.
Эти равенства называются формулами Виета.
Замечание. Формулы Виета справедливы и в том случае, если  и уравнение
и уравнение  имеет комплексные сопряженные корни.
имеет комплексные сопряженные корни.
Пример. В предыдущем параграфе показано, что уравнение  имеет корни
имеет корни  ,
, 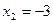 . Тогда
. Тогда 
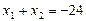 ,
,  .
.
Так как 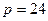 ,
, 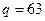 , то
, то  ,
, 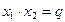 .
.
28. Решение квадратного уравнения 
Так как, по определению квадратного уравнения,  , то можно разделить на a обе части уравнения. Получим приведенное квадратное уравнение
, то можно разделить на a обе части уравнения. Получим приведенное квадратное уравнение  , в котором
, в котором  ,
,  . Тогда его корни можно найти по формуле
. Тогда его корни можно найти по формуле  .Получим:
.Получим:
 , или
, или

Число  называется дискриминантом квадратного уравнения
называется дискриминантом квадратного уравнения  (и дискриминантом квадратного трехчлена
(и дискриминантом квадратного трехчлена  ). Дискриминант показывает, сколько действительных корней имеет данное уравнение.
). Дискриминант показывает, сколько действительных корней имеет данное уравнение.
Если 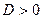 , то уравнение
, то уравнение  имеет два неравных действительных корня
имеет два неравных действительных корня 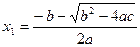 и
и  (
( ).
).
Если  , то уравнение
, то уравнение  имеет два равных действительных корня
имеет два равных действительных корня  .
.
Если  , то уравнение
, то уравнение  не имеет действительных корней.
не имеет действительных корней.
Замечание. В этом случае уравнение имеет два комплексных сопряженных корня
 и
и 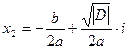 .
.
Пример 1. Решить уравнение  .
.
Решение. Так как  ,
,  (тогда
(тогда  ),
),  , то
, то
 .
.
Так как 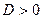 , то
, то  .
.
Тогда 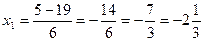 ,
,  .
.
Ответ: 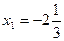 ,
,  .
.
Пример 2. Решить уравнение  .
.
Решение. Так как  ,
,  ,
,  , то
, то  .
.
Так как  , то данное уравнение не имеет действительных корней.
, то данное уравнение не имеет действительных корней.
29. Решение квадратных неравенств
 ,
,  ,
,  ,
, 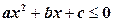
с положительным дискриминантом
сведением к системе двух линейных неравенств
Дискриминант квадратного трехчлена  -- это число
-- это число  .
.
Корнями квадратного трехчлена  называются корни уравнения
называются корни уравнения  .
.
Если 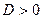 , то квадратный трехчлен
, то квадратный трехчлен  имеет два действительных корня
имеет два действительных корня 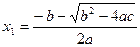 и
и  , причем
, причем  (значит
(значит  ).
).
Тогда его можно разложить на линейные множители:  .
.
Так как  , то можно разделить на a обе части каждого из рассматриваемых неравенств (если
, то можно разделить на a обе части каждого из рассматриваемых неравенств (если  , знак неравенства (то есть знак > или <) сохранится, если
, знак неравенства (то есть знак > или <) сохранится, если  , то знак неравенства поменяется на противоположный). В результате получится неравенство одного из видов:
, то знак неравенства поменяется на противоположный). В результате получится неравенство одного из видов:  ,
,  ,
,  ,
,  . Рассмотрим решение этих неравенств.
. Рассмотрим решение этих неравенств.
1) Произведение двух множителей положительно, если оба множителя положительные или оба множителя отрицательные, поэтому  , если
, если 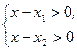 или
или 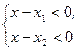 .
.
Решения обеих систем являются решениями данного квадратного неравенства.
Так как  ,то
,то 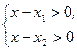



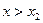 (тогда
(тогда 
 ).
).
Так как  , то
, то 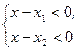

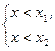

 (тогда
(тогда 
 ).
).
Ответ: неравенство  имеет множество решений, которое можно записать в виде
имеет множество решений, которое можно записать в виде  или
или 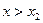 или в виде
или в виде  .
.
2) Аналогично получаем, что неравенство  имеет множество решений, которое можно записать в виде
имеет множество решений, которое можно записать в виде  или
или  или в виде
или в виде  .
.
3) Произведение двух множителей отрицательно, если один из множителей положительный, а другой отрицательный. Поэтому  , если
, если  или
или  .
.
Так как  , то
, то 



 .
.


 Эта система неравенств не имеет решений, так как число x не может быть одновременно меньше меньшего из двух чисел
Эта система неравенств не имеет решений, так как число x не может быть одновременно меньше меньшего из двух чисел  и
и  , и больше большего из них.
, и больше большего из них.
Ответ: неравенство  имеет множество решений, которое можно записать в виде
имеет множество решений, которое можно записать в виде  или в виде
или в виде  .
.
2) Аналогично получаем, что неравенство  имеет множество решений, которое можно записать в виде
имеет множество решений, которое можно записать в виде  или в виде
или в виде 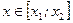 .
.
Пример. Решить неравенство  .
.
Решение. Найдем корни квадратного трехчлена  , то есть корни уравнения
, то есть корни уравнения  :
:  ,
,
 ,
,  .
.
Разложив левую часть данного неравенства по формуле  , получаем неравенство
, получаем неравенство  .
.
Так как 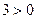 , то, разделив обе части последнего неравенства на 3, получаем равносильное ему неравенство
, то, разделив обе части последнего неравенства на 3, получаем равносильное ему неравенство  .
.
Произведение двух множителей отрицательно, если один из множителей положительный, а другой отрицательный. Поэтому решениями последнего неравенства являются решения каждой из систем неравенств если  или
или  . Тогда
. Тогда  или
или 


Графическое решение систем представлено на рисунках ( для первой системы рисунок слева, для второй справа). Видно, что вторая система решений не имеет, поэтому решениями данного неравенства являются только решения первой системы.
Ответ: 
30. Решение квадратных неравенств
 ,
,  ,
,  ,
, 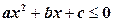
с использованием графика квадратичной функции
Замечание. Можно считать, что во всех этих неравенствах  . В противном случае, умножив обе части неравенства на
. В противном случае, умножив обе части неравенства на  и поменяв знак неравенства на противоположный, мы получим неравенство одного из указанных четырех видов, равносильное данному.
и поменяв знак неравенства на противоположный, мы получим неравенство одного из указанных четырех видов, равносильное данному.
Тогда графиком функции 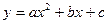 будет парабола, ветвь которой направлена вверх. Расположение этой параболы относительно оси абсцисс зависит от знака дискриминанта
будет парабола, ветвь которой направлена вверх. Расположение этой параболы относительно оси абсцисс зависит от знака дискриминанта  квадратного трехчлена
квадратного трехчлена  . Возможны 3 случая.
. Возможны 3 случая.



Рис. 1 Рис. 2 Рис. 3
Случай 1. Если 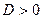 , то квадратный трехчлен
, то квадратный трехчлен  имеет два действительных корня
имеет два действительных корня 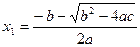 и
и  , причем
, причем  .Тогда парабола пересекает ось абсцисс в точках с абсциссами
.Тогда парабола пересекает ось абсцисс в точках с абсциссами  и
и  . Для строгих неравенств
. Для строгих неравенств  и
и 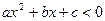 числа
числа  и
и  изображаются незакрашенными кружочками (как на рис.1). Для нестрогих неравенств
изображаются незакрашенными кружочками (как на рис.1). Для нестрогих неравенств  и
и  числа
числа  и
и  изображаются закрашенными кружочками. В этом случае:
изображаются закрашенными кружочками. В этом случае:
неравенство  имеет множество решений вида
имеет множество решений вида  ;
;
неравенство  имеет множество решений вида
имеет множество решений вида  ;
;
неравенство 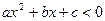 имеет множество решений вида
имеет множество решений вида  ;
;
неравенство  имеет множество решений вида
имеет множество решений вида  .
.
Случай 2. Если  , то квадратный трехчлен
, то квадратный трехчлен  имеет два равных действительных корня
имеет два равных действительных корня  . Тогда парабола касается оси абсцисс в точке с абсциссой
. Тогда парабола касается оси абсцисс в точке с абсциссой  . Для строгих неравенств
. Для строгих неравенств  и
и 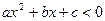 число
число  изображается незакрашенным кружочком (как на рис.2). Для нестрогих неравенств
изображается незакрашенным кружочком (как на рис.2). Для нестрогих неравенств  и
и  число
число  изображается закрашенным кружочком. В этом случае:
изображается закрашенным кружочком. В этом случае:
неравенство  имеет множество решений вида
имеет множество решений вида  ;
;
неравенство  имеет множество решений вида
имеет множество решений вида  ;
;
неравенство 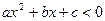 не имеет решений;
не имеет решений;
неравенство  имеет одно решение
имеет одно решение  .
.
Случай 3. Если  , то квадратный трехчлен
, то квадратный трехчлен  не имеет действительных корней. Тогда парабола не имеет общих точек с осью абсцисс (см. Рис. 3). В этом случае:
не имеет действительных корней. Тогда парабола не имеет общих точек с осью абсцисс (см. Рис. 3). В этом случае:
неравенства  и
и  имеют множество решений вида
имеют множество решений вида  ;
;
неравенства 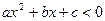 и
и  не имеют решений.
не имеют решений.
Пример. Решить неравенство  .
.
Решение. Умножив данное неравенство на  , получим равносильное ему неравенство
, получим равносильное ему неравенство  .
.
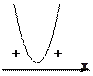 Квадратное уравнение
Квадратное уравнение 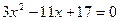 не имеет действительных корней, так как его дискриминант
не имеет действительных корней, так как его дискриминант  отрицательный. Поэтому графиком функции
отрицательный. Поэтому графиком функции  является парабола, не имеющая общих точек с осью абсцисс и расположенная в верхней полуплоскости относительно оси абсцисс (см. рис.). Из чертежа видно, что при любых значениях x функция принимает только положительные значения, поэтому неравенство
является парабола, не имеющая общих точек с осью абсцисс и расположенная в верхней полуплоскости относительно оси абсцисс (см. рис.). Из чертежа видно, что при любых значениях x функция принимает только положительные значения, поэтому неравенство  , а, следовательно, и данное неравенство, решений не имеет.
, а, следовательно, и данное неравенство, решений не имеет.
Ответ: решений нет.
31. Решение квадратных неравенств
 ,
,  ,
,  ,
, 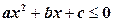
методом интервалов
Замечание. Можно считать, что во всех этих неравенствах  . В противном случае, умножив обе части неравенства на
. В противном случае, умножив обе части неравенства на  и поменяв знак неравенства на противоположный, мы получим неравенство одного из указанных четырех видов, равносильное данному.
и поменяв знак неравенства на противоположный, мы получим неравенство одного из указанных четырех видов, равносильное данному.



Рис. 1 Рис. 2 Рис. 3
Случай 1. Если 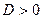 , то квадратный трехчлен
, то квадратный трехчлен  имеет два действительных корня
имеет два действительных корня 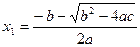 и
и  , причем
, причем  .Для строгих неравенств
.Для строгих неравенств  и
и 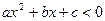 числа
числа  и
и  изображаются незакрашенными кружочками (как на рис.1). Для нестрогих неравенств
изображаются незакрашенными кружочками (как на рис.1). Для нестрогих неравенств  и
и  числа
числа  и
и  изображаются закрашенными кружочками. Точки
изображаются закрашенными кружочками. Точки  и
и  разбивают ось абсцисс на 3 интервала (см. рис. 1).
разбивают ось абсцисс на 3 интервала (см. рис. 1).
В этом случае:
неравенство  имеет множество решений вида
имеет множество решений вида  ;
;
неравенство  имеет множество решений вида
имеет множество решений вида  ;
;
неравенство 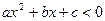 имеет множество решений вида
имеет множество решений вида  ;
;
неравенство  имеет множество решений вида
имеет множество решений вида  .
.
Случай 2. Если  , то квадратный трехчлен
, то квадратный трехчлен  имеет два равных действительных корня
имеет два равных действительных корня  . Обозначим
. Обозначим 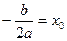 . Для строгих неравенств
. Для строгих неравенств  и
и 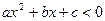 число
число  изображается незакрашенным кружочком (как на рис.2). Для нестрогих неравенств
изображается незакрашенным кружочком (как на рис.2). Для нестрогих неравенств  и
и  число
число  изображается закрашенным кружочком. Точка
изображается закрашенным кружочком. Точка  разбивает ось абсцисс на 2 интервала (см. рис. 2).
разбивает ось абсцисс на 2 интервала (см. рис. 2).
В этом случае:
неравенство  имеет множество решений вида
имеет множество решений вида  ;
;
неравенство  имеет множество решений вида
имеет множество решений вида  ;
;
неравенство 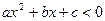 не имеет решений;
не имеет решений;
неравенство  имеет одно решение
имеет одно решение  .
.
Случай 3. Если  , то квадратный трехчлен
, то квадратный трехчлен  не имеет действительных корней, поэтому рассматривается только один интервал: вся числовая ось
не имеет действительных корней, поэтому рассматривается только один интервал: вся числовая ось  (см. Рис. 3).
(см. Рис. 3).
В этом случае:
неравенства  и
и  имеют множество решений вида
имеют множество решений вида  ;
;
неравенства 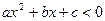 и
и  не имеют решений.
не имеют решений.
Пример. Решить неравенство  .
.
Решение. Найдем корни уравнения  :
:
 , т.е.
, т.е.  .
.
Точка  делит множество остальных
делит множество остальных  точек оси абсцисс на два интервала.
точек оси абсцисс на два интервала.
 Вычислим значения левой части неравенства в одной из точек каждого интервала. В первом интервале можно взять точку
Вычислим значения левой части неравенства в одной из точек каждого интервала. В первом интервале можно взять точку  , во втором – точку
, во втором – точку  . Находим:
. Находим:  и
и  . Таким образом, условию
. Таким образом, условию  удовлетворяет только одно число
удовлетворяет только одно число  . Оно и является решением данного неравенства.
. Оно и является решением данного неравенства.
Ответ:  .
.