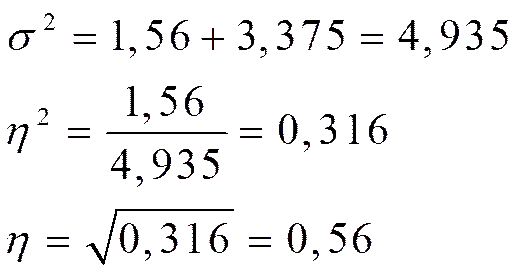 |
|
Правило сложения дисперсий
v общая дисперсия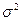 
измеряет вариацию результативного признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию:
v межгрупповая дисперсия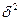 
характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки.
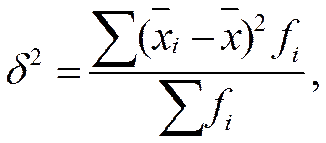
где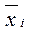 
- групповые средние;
- общая средняя по совокупности;
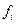- численности по отдельным группам.
v Внутригрупповая дисперсия 
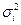отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она исчисляется следующим образом:
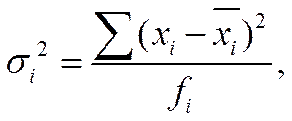
где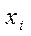 
- значение признака отдельной единицы в отдельной группе;
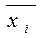- среднее значение признака в отдельной группе;
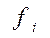- число единиц в отдельной группе
Внутригрупповые дисперсии, рассчитанные для отдельных групп, объединяются в средней величине внутригрупповой дисперсии:
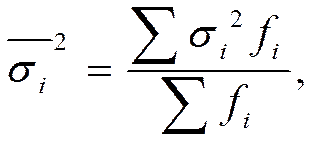
Правило сложения дисперсий:
Эмпирический коэффициент детерминации:
Показывает долю (удельный вес) вариации, обусловленной группировочным признаком в общей вариации результативного признака.
Эмпирическое корреляционное соотношение:
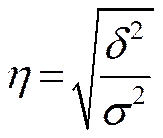
| Значения h | Теснота связи между группировочным признаком и результативным |
| До 0,3 | слабая |
| 0,3 - 0,5 | умеренная |
| 0,5 – 0,7 | заметная |
| 0,7 – 0,9 | тесная |
| 0,9 и более | очень сильная |
ПРИМЕР
Имеются данные о чистой прибыли (балансовой за вычетом налогов) предприятий двух районов:
| Районы | Число предприятий | Чистая прибыль, млн руб. |
| I | 4, 6, 9, 4, 7, 6 | |
| II | 8, 12, 8, 9, 6, 5, 7, 7, 8, 10 |
Определите дисперсии чистой прибыли: а) групповые (по каждому району); б) среднюю из групповых; в) межгрупповую; г) общую. Сделайте выводы о зависимости между месторасположением и финансовым результатом предприятия.
Решение
1) расчет дисперсий внутри каждой группы:
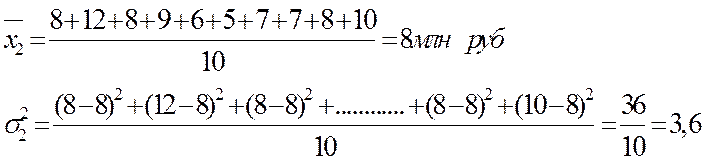
2) расчет средней из внутригрупповых дисперсий:
3) расчет межгрупповой дисперсии:
4) анализ взаимосвязи признаков:
