Главная | Обратная связь

Свойства спектральной плотности

1. g(w)³0

2.

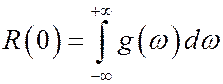
3. Для вещественных СП g(w)=g(-w), т.е. g(w) - четная функция.

Из теории преобразований Фурье следует, что если 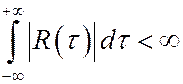, то

.

То есть g(w) и R(t) есть пара, связанная преобразованием Фурье.

Для вещественного СП и g(w) и R(t) – четные функции и формулы взаимных преобразований имеют вид

,

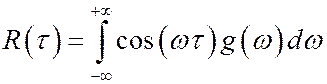Пример 1.

Пусть x(t)= x*cos(lt)+h*sin(lt), где x,h – некоррелированные с.в. с нулевыми средними и единичными дисперсиями, а l– постоянная.

Найти корреляционную и спектральную функции СП.

Решение.

R(u)=Mx(t+u)x(t)=M[x*cos(l(t+u))+h*sin(l(t+u))]*[x*cos(lt)+h*sin(lt)]=

=M[x²*cos(l(t+u))cos(lt)+

+xh(cos(l(t+u))sin(lt)+sin(l(t+u))cos(lt))+h²*sin(l(t+u))sin(lt)]=

= cos(l(t+u))cos(lt)+ sin(l(t+u))sin(lt)= cos(lu)

Т.О. процесс стационарен в широком смысле.

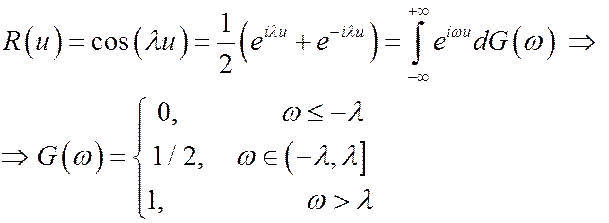
Пример 2.

Пусть 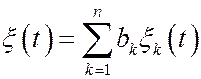, где x_k(t)= x_kcos(l_kt)+h_ksin(l_kt), где x_k,h_k – некоррелированные с.в. (Mx_kh_k=0 и Mx_ix_j=Mh_ih_j=0 при i¹j) с нулевыми средними и единичными дисперсиями, а l_k – постоянные.

Проводя аналогичные выкладки, легко подсчитать, что .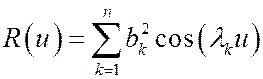

При этом спектральная функция СП G(w) растет только в точках ±l_k и имеет в них скачки .

СП, для которых функция G(w) растет только скачками, называются процессами с дискретным спектром.

СП, имеющие спектральную плотность g(w) называются процессами с непрерывным спектром.

Т.О. стационарный процесс 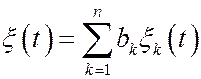является процессом с дискретным спектром.

Верно и обратное утверждение: всякий процесс с дискретным спектром представим в виде

.

 

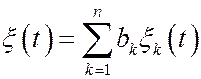Физический смысл спектра случайного процесса близок к смыслу спектра детерминированных сигналов. Если мы разложим детерминированный сигнал в ряд Фурье (или представим его виде интеграла Фурье), то квадраты модулей коэффициентов Фурье представляют энергии сигналов по различным частотам. При этом спектральная плотность g(w) представляет собой среднюю (по всем реализациям) энергию СП, приходящуюся на интервал (w, w+Dw).

Дадим грубую интерпретацию этого факта. Для этого введем понятие интеграла от СП

,

где f(t) – некоторая детерминированная функция. Этот интеграл определяется как предел интегральных сумм

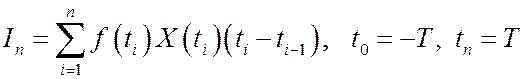
при 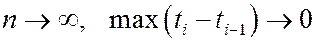и дает некоторую случайную величину. Сходимость интегральных сумм I_n к с.в. I означает следующее: 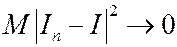при n®¥.

Теорема. Для существования интеграла 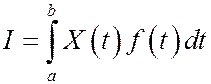достаточно, чтобы существовал интеграл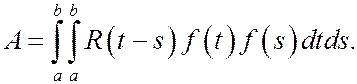

При этом .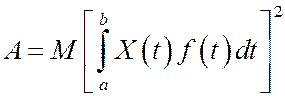

Рассмотрим интеграл .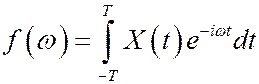

Здесь f(w) есть случайная функция частоты. Среднее нормированное значение квадрата модуля этой функции 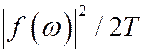представляет собой энергию СП, приходящуюся на интервал (w, w+Dw), где Dw~1/2T. Произведем усреднение величины 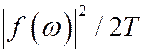и получим:

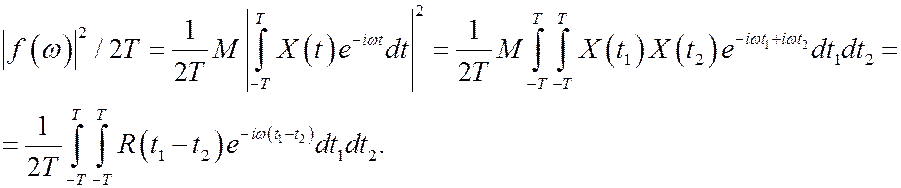
При T®¥ последний интеграл стремится к .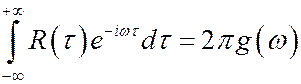

Т.О. мы показали, что спектральная плотность g(w) пропорциональна средней (по всем реализациям) энергии СП, приходящейся на интервал (w, w+Dw).