 |
|
ДІЙСНИЙ ЕВКЛІДОВИЙ ПРОСТІР
Лінійний простір над полем дійсних чисел називається дійсним евклідовим простором, якщо в ньому визначена операція скалярного добутку двох будь-яких векторів, тобто будь-якій парі векторів  і
і  простору ставиться у відповідність дійсне число
простору ставиться у відповідність дійсне число  . При цьому для будь-яких векторів простору повинні виконуватися умови (аксіоми).
. При цьому для будь-яких векторів простору повинні виконуватися умови (аксіоми).
1.  =
= 
2. 
3.  ,
, 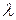 – число
– число
4.  , лише при
, лише при 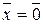
 .
.
Розглянемо приклади евклідових просторів.
1. Векторний простір направлених відрізків над полем дійсних чисел, в якому введений таким чином скалярний добуток двох довільних векторів  і
і 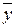
 =
= 

 ,
, 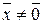 ,
,  (
(  – кут між
– кут між  і
і 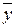 ),
), 
 =0, якщо
=0, якщо  =
=  або
або 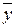 =
=  ,
,
є дійсним евклідовим простором, оскільки виконуються всі аксіоми скалярного добутку.
2. Нехай С 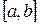 – множина всіх неперервних на відрізку
– множина всіх неперервних на відрізку 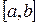 дійсних функцій. Ця множина є лінійним простором над полем дійсних чисел. Простір стане евклідовим, якщо кожній парі функцій
дійсних функцій. Ця множина є лінійним простором над полем дійсних чисел. Простір стане евклідовим, якщо кожній парі функцій  і
і 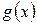 із множини С поставити у відповідність число
із множини С поставити у відповідність число
 =
= 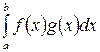 .
.
Всі вимоги, що пред'являються до скалярного добутку, виконуються.
Теорема 1.1. Для будь-яких двох векторів  і
і 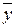 дійсного евклідового простору
дійсного евклідового простору  (нерівність Коші-Буняковского).
(нерівність Коші-Буняковского).
Лінійний простір називається нормованим, якщо кожному вектору  цього простору поставлено у відповідність число
цього простору поставлено у відповідність число  , яке називається нормою вектору або його довжиною. При цьому повинні виконуватися умови (аксіоми норми)
, яке називається нормою вектору або його довжиною. При цьому повинні виконуватися умови (аксіоми норми)
1.  , причому
, причому  , лише коли
, лише коли  ;
;
2.  – нерівність трикутника;
– нерівність трикутника;
3.  для любого числа
для любого числа 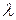 .
.
Всякий евклідовий простір можна вважати нормованим, якщо кожному вектору  простору поставити у відповідність число
простору поставити у відповідність число  . Щоб переконатися в цьому, потрібно перевірити виконання всіх аксіом норми. Перша і третя аксіоми норми виконуються, оскільки по першій властивості скалярного добутку
. Щоб переконатися в цьому, потрібно перевірити виконання всіх аксіом норми. Перша і третя аксіоми норми виконуються, оскільки по першій властивості скалярного добутку  , причому
, причому 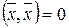 лише при
лише при 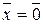 , тобто
, тобто  , лише коли
, лише коли  , а по третій властивості
, а по третій властивості  , тобто
, тобто  . Аксіома трикутника також виконується. Дійсно,
. Аксіома трикутника також виконується. Дійсно,  . Згідно нерівності Коші – Буняковского
. Згідно нерівності Коші – Буняковского  . Отже,
. Отже,  .
.
По аналогії з випадком тривимірного простору направлених відрізків введемо поняття кута між двома векторами евклідового простору. Під кутом між яким – небудь ненульовими векторами  і
і 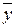 простору розуміється таке число
простору розуміється таке число  , що
, що 
 ,
,  ,
,  .
.
Це визначення коректне, оскільки згідно з нерівністю Коші – Буняковского  , тому дріб, що визначає значення
, тому дріб, що визначає значення  по модулю менше одиниці. Отже, які б не були ненульові вектори
по модулю менше одиниці. Отже, які б не були ненульові вектори  і
і 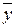 евклідового простору, існує єдине число
евклідового простору, існує єдине число  , що визначає кут між векторами
, що визначає кут між векторами  і
і 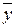 .
.
Приклад. Нехай 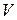 – евклідовий простір, елементами якого є дійсні функції, неперервні на відрізку
– евклідовий простір, елементами якого є дійсні функції, неперервні на відрізку  . Скалярний добуток двох довільних елементів
. Скалярний добуток двох довільних елементів  и
и  простору
простору 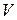 визначимо відомим способом
визначимо відомим способом  .
.
Потрібно знайти кут між елементами 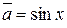 и
и  .
.
Розв’язання:
Згідно з визначенням скалярного добутку 
 .
.
На основі формули 
 ,
,  ,
, 
 , отже, кут між елементами
, отже, кут між елементами  і
і  простору
простору 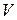 дорівнює
дорівнює  .
.
Два вектори  і
і 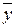 евклідового простору називаються ортогональними, якщо їх скалярний добуток
евклідового простору називаються ортогональними, якщо їх скалярний добуток  . Суму
. Суму  +
+ 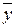 двох ортогональних векторів і називатимемо гіпотенузою прямокутного трикутника
двох ортогональних векторів і називатимемо гіпотенузою прямокутного трикутника  і
і 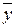 .
.
Теорема Піфагора. Квадрат довжини гіпотенузи прямокутного трикутника дорівнює сумі квадратів довжин катетів.