Главная | Обратная связь

Механическая вселенная

 

Опубликовав «Рассуждения и математические доказательства, касающиеся двух новых наук», Галилей подвел человеческую культуру к границе нового мира. Исаак Ньютон сделал последние великанские шаги и по ходу дела завершил построение системы совершенно нового мышления. Вслед за Ньютоном наука отказалась от Аристотелева взгляда на природу, движимую предназначением, и приняла Вселенную Пифагора, движимую числами. Вслед за Ньютоном, ионийское утверждение, что мир можно понять посредством наблюдения и рассуждения, преобразилось в метафору: мир подобен часам, его механизмами управляют численные законы, придающие любому аспекту природы – включая, как многие считали, и взаимодействия между людьми – полную предсказуемость.

В далекой Америке отцы-основатели страны приняли Ньютоново мировоззрение вдобавок к теологии и закрепили в Декларации независимости, что «законы природы и ее Бога наделяют»[184]людей правом на политическое самоопределение. Во Франции после Революции с ее неприятием науки Пьер-Симон де Лаплас поднял Ньютонову физику на новый уровень математической сложности и заявил, что, применяя теорию Ньютона, высокоразвитый интеллект способен «объять одной и той же формулой движения и величайшие тела во Вселенной, и мельчайшие атомы – ничто для него не останется неопределенным, и будущее, как и прошлое, явлено будет взгляду его».

Ныне мы все рассуждаем по-ньютоновски. Мы говорим о силе применительно к человеческому характеру и об ускорении – к распространению заболевания. Мы говорим о физической или даже умственной инерции и об импульсе, приобретенном спортивной командой. Мыслить в таких понятиях до Ньютона было непредставимо, не мыслить в таких понятиях непредставимо в наши дни. Даже те, кто ничего не слыхал о законах Ньютона, взращены на его взглядах. И потому изучать работы Ньютона означает изучать наши собственные корни.

Поскольку мировоззрение Ньютона для нас совершенно естественно, чтобы оценить потрясающий гений его творения, нужно хорошенько постараться. В средней школе, когда мне впервые рассказали про «законы Ньютона», они показались мне настолько простыми, что я удивился, с чего такой сыр-бор. Странное дело: чтобы придумать нечто, понятное мне, пятнадцатилетнему мальчишке, за пару уроков, понадобился один из умнейших людей в истории науки – и многолетний труд. Как вышло, что совершенно доступные для меня представления оказались труднейшими для понимания несколько столетий назад?

Мой отец, кажется, понял, почему. Я рассказываю своим детям историю про «Пост-ит», а мой отец обычно обращался к преданьям старины. Когда люди смотрели на мир сотни лет назад, говорил он мне, они видели действительность совсем не так, как мы воспринимаем ее сегодня. Он рассказывал мне о временах, когда, еще подростками в Польше, они с друзьями набрасывали на козу простыню и загоняли ее в дом. Старшие родственники думали, что это привидение. Ладно, дело было на еврейский праздник Пурим, а старшие были изрядно пьяны, но отец объяснял их реакцию не опьянением: он говорил, что они истолковывали увиденное в контексте своих верований, а привидения были привычной их частью. Я, может, считаю это невежеством, говорил он, но то, что Ньютон сказал миру о математических законах Вселенной, вероятно, казалось людям того времени столь же странным, сколь привидения – мне. Так и есть: ныне, даже если вы никогда не изучали физику, дух Исаака Ньютона хоть самую малость, но в вас есть. Но не вырасти мы в Ньютоновой культуре, те законы, что вроде бы самоочевидны, были бы для большинства из нас непостижимы[185].

 

* * *

 

Описывая незадолго до смерти свою жизнь, Ньютон так характеризовал свой вклад в науку: «Мне неизвестно, кем я кажусь миру, но сам себя я вижу мальчишкой, который играл на берегу моря и радовался, находя камешек глаже или ракушку красивее прочих, а великий океан истины раскинулся предо мной, непознанный»[186].

На любом из Ньютоновых камешков ученые менее одаренные и плодовитые могли бы сделать потрясающую карьеру. Помимо работ, посвященных силе тяготения и движению, он отдал много лет раскрытию тайн оптики и света, изобрел известную нам ныне физику, а заодно и математический анализ. Когда я изложил все это отцу, который до того, как я взялся изучать работы Ньютона, и не слыхал о нем, отец нахмурился и сказал: «Не будь как он. Занимайся чем-нибудь одним!» Поначалу я отнесся к этому наставлению с той разновидностью высокомерия, в которой подростки большие мастера. Но вообще-то отец в некотором смысле дело говорил. Ньютон подошел опасно близко к тому, чтобы стать гением, который за все берется и ничего не доводит до конца. К счастью, как мы знаем, вмешался рок, и Ньютон ныне считается провозвестником всей революции мышления.

Одного Ньютон не делал никогда – не играл на морском берегу. Хоть он и извлек немало пользы из эпизодического общения с учеными и в Британии, и на континенте, зачастую – почтой, он никогда не покидал окрестности небольшого треугольника, связывавшего его родной Вулсторп, его университет в Кембридже и Лондон. Да и вообще не «играл» он – ни в каком смысле слова из тех, какие мы в него вкладываем. Ньютон обошелся в жизни без друзей и родственников, с которыми он ощущал бы близость, не было в его жизни места даже для какой-нибудь возлюбленной, хоть одной: по крайней мере, до его более взрослых лет заставить Ньютона общаться было примерно равносильно попытке уговорить котов сыграть в «Скрэббл». Вероятно, точнейшим можно считать замечание одного дальнего родственника, Хамфри Ньютона, трудившегося у него помощником пять лет: он сказал, что Ньютон рассмеялся всего раз – когда кто-то спросил его, зачем вообще изучать Евклида.

Ньютоном владела чистая безучастная страсть понимать мир, а не желание сделать его лучше на благо человечеству. Он достиг великой славы при жизни, но разделить ее ему было не с кем. Добился интеллектуальных побед, но никак не любви. Принял высочайшие звания и почести, но большую часть времени посвятил интеллектуальным сварам. Было бы мило иметь основания утверждать, что этот исполин интеллекта был сердечным, приятным человеком, но, если и были у него подобные наклонности, он изрядно постарался их подавить и являть себя миру высокомерным мизантропом. Он был из тех людей, какие, заметь вы при них, что день сер, скажут: «Нет, небо на самом деле голубое». Что еще неприятнее – он мог это доказать. Физик Ричард Фейнман (1918–1988) выразил эти чувства многих погруженных в себя ученых, написав книгу «Не все ли равно, что думают другие?»1. Ньютон не написал мемуаров, однако, случись такое, он, вероятно, назвал бы их «Надеюсь, я как следует вас достал» или, может, «Отвяжись от меня, болван».

Стивен Хокинг однажды сказал мне, что в этом смысле он рад своему параличу: тот позволил сильнее сосредоточиться на работе. Полагаю, Ньютон мог бы сказать, по той же причине, какие восхитительные преимущества дает жизнь полностью в своем собственном мире – не расходуя время, не делясь им с кем-то еще. На самом деле, недавние исследования показали, что у одаренных в математике студентов значительно больше склонности к научной карьере, если им недостает навыков общения[187]. Я тоже давно подозревал, что неспособность общаться впрямую связана с успехом в науке. Уж во всяком случае мне известно несколько состоявшихся ученых, которых сочли слишком странными для работы где угодно, кроме больших исследовательских учреждений. Один коллега-аспирант надевал день за днем одни и те же штаны и белую футболку, хотя поговаривали, что у него два таких набора, и поэтому одежде время от времени перепадала стирка. Еще один коллега, знаменитый профессор, был настолько стеснителен, что обычно отводил глаза, говорил очень тихо и отступал на шаг, если замечал, что вы стоите к нему ближе четырех футов. Две последние особенности затрудняли послесеминарское общение, поскольку профессора было почти не слышно. При нашей первой встрече, еще когда я был студентом, я оплошал и подошел слишком близко, а затем продолжал надвигаться на него, пока тот ретировался, и в результате бедняга чуть не упал, наткнувшись на стул.

Наука – предмет потрясающей красоты. Но, хотя развитие науки требует перекрестного опыления мыслями, какое может случиться лишь при взаимодействии с другими творческими умами, оно требует и долгих уединенных часов, что может представляться однозначным преимуществом тем, кто не склонен к общению или даже предпочел бы жить совсем отдельно. Как писал Альберт Эйнштейн, «одна из сильнейших мотиваций, какие толкают людей в искусства и науки, – побег от повседневной жизни с ее мучительной грубостью и безнадежной скукой… Всяк делает это мироздание и его сотворение стержнем своей эмоциональной жизни, чтобы так обрести покой и уверенность, какие не находятся в тесном водовороте личного опыта»[188].

Ньютоново презрение к повседневным заботам мира позволило ему заботиться о своих интересах и нимало не отвлекаться, но также заставило его скрыть значительную часть своей научной работы – он решил не издавать огромный массив своих изысканий. К счастью, он от них и не избавлялся – был таким барахольщиком, что заслужил бы личного реалити-шоу, однако Ньютон копил не скелеты домашних животных, старые журналы или обувь, из которой вырос еще в семь лет, а записи обо всем на свете – от математики, физики, алхимии, религии и философии до отчетов о каждом потраченном пенни и описаний своих чувств к родителям.

Ньютон сберег практически все, что написал за жизнь, – даже листки с никчемными расчетами и старые школьные тетради, – позволив тем, кто желал копаться, постичь в беспрецедентных подробностях эволюцию Ньютоновых взглядов. Большая часть его научных бумаг досталась библиотеке Кембриджа, его интеллектуального дома. Но другие документы, в общей сложности включающие миллионы слов, были постепенно распроданы на аукционе Сотби, где экономист Джон Мэйнард Кейнс [Мейнэрд Кинз], участвуя в торгах, скупил почти все труды Ньютона по алхимии.

Биограф Ньютона Ричард Уэстфолл посвятил двадцать лет изучению жизни ученого и пришел к заключению, что Ньютона «нельзя оценивать по критериям, с которыми мы подходим к пониманию людей»[189]. Но даже если Ньютон был инопланетянином, он по крайней мере оставил нам своим дневники.

 

* * *

 

Ньютоново стремление понять мир происходило от чрезвычайной любознательности – мощного побудителя к открытиям, какой исходил словно бы полностью изнутри, подобно импульсу, толкнувшему моего отца обменять кусок хлеба на математическую разгадку. Но в случае Ньютона эту тягу питало что-то иное. Хотя ему поклоняются как идеалу научной рациональности, его интерес к природе Вселенной был, как и у всех вплоть до обитателей Гёбекли-Тепе, сложно переплетен с духовностью и религией. Ньютон верил, что Бог явлен нам и в слове его, и в деле[190], и потому изучение законов природы есть изучение Бога, а рвение в науке – разновидность религиозного пыла.

Ньютонова тяга к уединению и многие часы ежедневной работы – большое преимущество, по крайней мере, для его интеллектуальных достижений. Однако, хоть его затворничество в пространстве ума стало для науки настоящим подарком, сам Ньютон заплатил за них дорого, и, похоже, это результат болезненного детства, проведенного в одиночестве.

Учась в школе, я сочувствовал детям, которые никому не нравились, особенно потому, что сам был таким. Ньютону пришлось еще хуже. Он не нравился собственной матери. Он появился на свет 25 декабря 1642 года эдаким непрошенным рождественским подарком. Отец умер за несколько месяцев до этого, а мать Анна [Ханна], вероятно, полагала, что существование Исаака – лишь краткосрочное неудобство, поскольку родился он недоношенным и вряд ли бы выжил. Более восьмидесяти лет спустя Ньютон сказал мужу своей племянницы, что при рождении был так мал, что поместился бы в квартовый горшок, и так слаб, что потребовался валик на шею – удерживать голову на плечах. Так скверно шли дела у маленького болванчика, что женщины, отправленные за пару миль добыть припасы, не слишком торопились – были уверены, что ребенок к их возращению уже будет мертв. Но они ошиблись. Для сохранения младенцу жизни не понадобилось никаких других технических ухищрений, кроме валика.

Может, Ньютон не видел никакого смысла в людях в своей жизни потому, что его мать никогда, похоже, не видела смысла в нем самом. Когда ему было три, она вышла замуж за богатого ректора, преподобного Барнэбэса Смита. Преподобный Смит был старше Ханны в два с лишним раза, ему хотелось юной жены – но не юного пасынка.

Нельзя сказать наверняка, к какому духу в семье это могло привести, однако более или менее уверенно можно предположить, что некое напряжение имелось, поскольку, много лет спустя, в записях о детстве Ньютон вспоминает, что «угрожал отцу и матери Смит сжечь и их, и дом вместе с ними»[191]. Исаак не сообщает, как родители отозвались на его угрозу, однако известно, что вскоре его услали прочь и вверили заботам бабушки. Та с Исааком ладила получше, но много ль ему было надо. Близки они точно не были – нигде в записях и черновиках, оставшихся после Ньютона, нет ни единого нежного воспоминания о прародительнице. Впрочем, мило, что нет и воспоминаний о том, как он хотел ее поджечь и спалить дотла ее дом.

Когда Ньютону было десять, преподобный Смит помер, и Исаак ненадолго вернулся домой, где теперь обитало еще трое детей его матери от второго брака. Через пару лет после смерти Смита Ханна отправила старшего сына в пуританскую школу в Грэнтэм, в восьми милях от Вулсторпа. Учась в Грэнтэме, Ньютон жил в доме аптекаря и химика по имени Уильям Кларк; тот восхищался Ньютоном и поддерживал в нем изобретательность и любопытство. Юный Исаак научился толочь химические вещества пестиком в ступке, измерял силу штормового ветра, прыгая по направлению его и против и сравнивая потом длину прыжка, мастерил маленькие мельницы с приводом от колеса, которое крутила мышь, а также четырехколесную телегу, которую приводил в движение, сидя в ней и крутя ручку. А еще сделал воздушного змея, к хвосту которого привязал светильник и запускал по ночам, пугая соседей.

С Кларком-то Ньютон ладил, а вот одноклассники – другая история. В школе Ньютон, со всей очевидностью не похожий на остальных и интеллектуально превосходивших всех, вызывал к себе то же отношение, что возникает в таких случаях и в наши дни: другие дети его терпеть не могли. Одинокая, но крайне творческая жизнь, которую он вел, когда был мальчишкой, готовила его к творческой, но мучительной и одинокой судьбе, большую часть его зрелости отнюдь не счастливой.

Ближе к семнадцати годам Ньютона мать забрала его из школы, желая, чтобы сын вернулся домой – управлять имением. Но хозяйственник из Ньютона вышел не лучший, что доказывает: можно быть гением и рассчитывать орбиты планет – и полным растяпой, когда дело доходит до выращивания люцерны. Более того – хозяйство его и не интересовало. Пока изгороди в его владениях приходили в негодность, а свиньи носились по кукурузным посадкам, Ньютон мастерил водяные колеса на ручье или же просто читал. Как пишет Уэстфолл, Ньютон протестовал против жизни, которую проводят, «пася овец или гребя навоз»[192]. Как и большинство знакомых мне физиков.

К счастью, вмешались дядя Ньютона и директор Грэнтэмской школы. Распознав в нем гения, в июне 1661 года они отправили его в Колледж Св. Троицы в Кембридже. Там он познакомился с научным мышлением своего времени – лишь для того, чтобы в один прекрасный день восстать и свергнуть его. Слуги праздновали его отбытие – не потому что радовались за него, а потому что он сурово с ними обращался. С таким характером, считали они, место ему лишь в университете.

 

* * *

 

Кембридж для Ньютона более чем на три с половиной десятка лет стал домом и стартовой площадкой умственной революции, которую он запустил. Хотя эту революцию часто изображают как череду озарений, борьба за тайны Вселенной, которую вел Ньютон, скорее походила на окопную войну – одна тяжкая интеллектуальная битва за другой, и в этой войне каждую пядь земли приходилось присваивать постепенно и ценой громадных вложений сил и времени. Гений меньшего калибра или меньшей фанатической приверженности такую борьбу вести бы не смог.

Поначалу даже условия жизни Ньютона были для него испытанием. Мать наделила его стипендией всего в десять фунтов, хотя сама получала неплохой ежегодный доход в семьсот с лишним. Такая стипендия поместила Ньютона в самые низы общественного устройства Кембриджского университета.

Стипендиат («сайзер»), в жесткой кембриджской иерархии, – бедный студент, не плативший за еду и обучение и получавший небольшие карманные деньги, обслуживая более состоятельных учащихся: причесывая их, чистя им обувь, принося им хлеб и пиво и опорожняя их ночные горшки. Стать стипендиатом для Ньютона было повышением в должности – начинал он с субстипендиата, а это означало ту же черновую работу, что и у стипендиата, только субстипендиаты сами платили за еду и посещаемые лекции. Свыкнуться с положением слуги у мальчишек того же племени, что измывались над ним в Грэнтэмской школе, было для Ньютона явно непросто. В Кембридже он, что называется, нюхнул жизни «под лестницей».

В 1661 году Галилеевым «Рассуждениям и математическим доказательствам, касающимся двух новых наук» было всего двадцать лет, и, как и многие другие работы Галилея, эта на кембриджскую учебную программу заметного влияния тогда еще не оказала. Это означало, что в обмен на услуги и плату Ньютону предлагали уроки, включавшие в себя все, что ученые – приверженные Аристотелю – знали о мире: Аристотелеву космологию, Аристотелеву физику, Аристотелеву риторику… Ньютон читал Аристотеля в подлиннике, изучал учебники по дисциплинам Аристотеля, копался во всех книгах, положенных по программе. Ни одну так и не дочитал, поскольку, подобно Галилею, не счел доводы Аристотеля убедительными.

И все же труды Аристотеля являли первый изощренный подход к знанию, с каким столкнулся Ньютон, и потому, даже опровергая его, он из самого этого опровержения извлек урок, как нужно подходить к разнообразным вопросам природы и думать о них организованно и последовательно – и с потрясающей неукоснительностью. Ньютон, убежденный холостяк, редко включавшийся в потехи и досуги, трудился больше, чем кто угодно в пределах моего знания, – по восемнадцать часов в день, семь дней в неделю. Эту привычку он поддерживал многие десятилетия подряд.

Не приняв ничего из Аристотелевых трудов, включенных в программу Кембриджа, Ньютон начал свое долгое странствие к новому мировоззрению в 1664 году: в его записях отмечается, что он взялся создать собственную программу обучения, читая и осмысляя работы великих современных европейских мыслителей, включая Кеплера, Галилея и Декарта. Хоть и не блистательно, однако Ньютон все же закончил в 1665 году университет и получил титул исследователя, а также финансовую поддержку на следующие четыре года дополнительного образования.

А летом 1665 года Кембридж накрыло внезапной страшной волной чумы, и заведение закрыли вплоть до весны 1667-го. Пока учиться было негде, Ньютон вернулся в отчий дом в Вулсторпе и продолжил трудиться в одиночестве. В некоторых изложениях 1666 год именуется Ньютоновым annus mirabilis[193]. По этим преданиям, Ньютон сидел в семейном поместье, изобретал математический анализ, разбирался с законами движения, а затем, увидев падающее яблоко, открыл закон всемирного тяготения.

Что верно, то верно, год вышел недурной. Но все происходило не так. Теория всемирного тяготения сложилась не вот так запросто, единой блестящей мыслью, какую можно ухватить благодаря озарению, – это целый корпус трудов, сформировавшийся вокруг совершенно новой научной традиции[194]. Более того, от картинки из учебника, изображающей Ньютона и яблоко, один вред, потому что из-за нее создается впечатление, будто физики добиваются результатов благодаря громадным внезапным прозрениям: кому-нибудь эдак дали в лоб, и у него от этого открылся дар предсказывать погоду. В действительности, даже в случае с Ньютоном, чтобы чего-то добиться, нужно было получить по лбу много-много раз, провести много-много лет в осмыслении собственных соображений и прийти наконец к подлинному пониманию их потенциала. Мы, ученые, терпим от этих ударов по лбу головную боль, потому что, как и футболистам, спорт нравится нам больше, чем не нравится из-за него страдать.

Вот почему большинство историков сомневается в истории с чудесным озарением: прозрения Ньютона в физике во время чумного периода случились не все скопом, а за три года – с 1664 по 1666-й. Более того, никакой ньютонианской революции в конце этого периода не случилось: в 1666 году сам Ньютон еще не был ньютонианцем. Он все еще считал, что равномерное движение возникает из чего-то присущего движущемуся телу изнутри, а под «гравитацией» понимал некое внутреннее свойство, возникающее в материи, из которой создано тело, а не внешнюю силу, исходящую от Земли. Представления, развитые им в тот период, – лишь начало, кое ввергло его в растерянность и брожение ума на самые разные темы, включая силу, гравитацию и движение, то есть обо всех ключевых понятиях, которые в конце концов объединятся в предмет его великого труда – «Philosophi ce Naturalis Principia Mathematica».

Мы довольно неплохо знаем, о чем думал Ньютон у себя в имении в Вулсторпе, поскольку он по своему обыкновению записывал это в громадную, почти не использованную тетрадь, доставшуюся от преподобного Смита. Ньютону с той тетрадью повезло, а в более зрелые годы повезло располагать бумагой в достатке, чтобы записать миллионы слов и математических выражений, в которые он облек свои работы.

Я помянул нововведения вроде университетов и применения математических уравнений, но были и другие невоспетые подспорья научной революции, которые мы воспринимаем как должное, и среди них следует отдельно отметить возросшую доступность бумаги. К удаче Ньютона, первая коммерчески успешная мануфактура по производству бумаги в Англии была основана в 1588 году. Не менее важно и то, что Королевская почта в 1635 году начала обслуживать частные отправления, что позволило нелюдиму Ньютону общаться на бумаге с другими учеными даже из очень дальних краев. Но бумага во дни Ньютона по-прежнему стоила недешево, и потому он дорожил своей тетрадью, которую называл «Черновой книгой». В ней – подробности Ньютонова подхода к физике движения, редкая возможность увидеть, как развивается мысль в блистательном уме.

Мы, к примеру, знаем, что 20 января 1665 года Ньютон начал записывать в «Черновой книге» развернутое математическое – а не философское – расследование движения. Ключевой для этого расследования была разработка математического анализа – новой разновидности математики, задуманной для изучения меняющихся величин.

Продолжая традицию Орема, Ньютон представлял себе изменение как наклонную линию. Допустим, если отражать на графике расстояние, пройденное телом, на вертикальной оси, а время – на горизонтальной, тогда наклонная линия на графике – отображение скорости тела. Горизонтальная линия, таким образом, представляет неизменное положение тела, а наклонная или кривая показывает, что положение тела резко меняется – тело движется с большой скоростью.

 

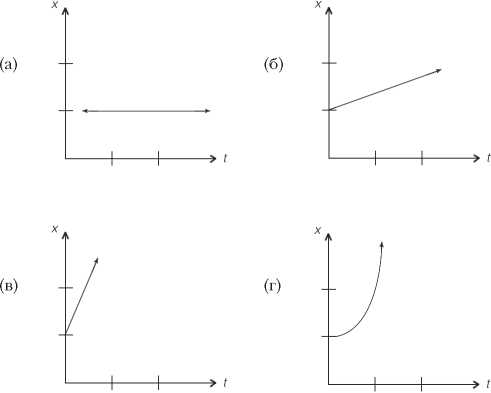
Графики (а), (б) и (в) изображают равномерное движение с (а) нулевой скоростью (тело покоится), (б) малой скоростью,(в) большой скоростью. График (г) отражает движение с ускорением

 

Но Орем и другие толковали графики в более качественном смысле, нежели мы в наши дни. Про график «расстояние-время», например, не понимали, что он в каждой точке представляет расстояние, пройденное за время, равное координате на горизонтальной оси. Не понимали и того, что наклон линии на графике представляет скорость тела в каждый момент времени. До Ньютона скорость для физиков была средней, то есть все пройденное расстояние, деленное на продолжительность времени в пути. То были довольно грубые расчеты, поскольку время в них обычно исчислялось часами, днями или даже неделями. Вообще-то засекать короткие промежутки времени с хоть какой-то точностью было и невозможно – вплоть до 1670 года, когда английский часовщик Уильям Клемент изобрел маятниковые «ходики», благодаря которым время стало можно измерять с точностью до секунды.

Пойти дальше средних величин к значениям графиков и их уклонов в каждой отдельной точке – вот откровение Ньютонова анализа. Он взялся разбираться с тем, с чем никто до него не возился: как определить мгновенную скорость тела, ее скорость в каждый миг? Как разделить расстояние, пройденное телом, на затраченное время, если речь идет о временном промежутке размером с точку? Мыслимо ли это вообще? Эту задачу Ньютон и взялся решать в «Черновой книге».

Галилей воображал себе «предельные случаи» – например, плоскость, чей угол наклона все увеличивают и увеличивают, пока он не достигнет прямого, Ньютон же довел этот подход до предела возможности. Чтобы определить мгновенную скорость в данный момент времени, он представил, как будет рассчитывать среднюю скорость традиционно, то есть за некоторый промежуток времени, включая и то мгновение, которое его интересует. Затем он представил себе нечто новое и абстрактное: сужение этого промежутка, еще и еще, пока, в предельном случае, его протяженность не приблизится к нулю.

Иными словами, Ньютон представил, что временной промежуток можно взять столь малым, что он будет меньше любого конечного числа – но все-таки больше нуля. Ныне длина такого промежутка называется «стремящейся к нулю» или «бесконечно малой». Если рассчитать среднюю скорость в определенный промежуток времени, а затем уменьшить этот промежуток до бесконечно малого, получится скорость тела в определенный миг, или мгновенная скорость.

Математические правила нахождения мгновенной скорости в данный момент времени – или, в общем случае, наклона линии в данной точке – и есть основа математического анализа[195]. Если атомы – неделимые составляющие химических веществ, то бесконечно малые величины – своего рода неделимые составляющие пространства и времени.

Вместе с математическим анализом Ньютон изобрел математику изменения. В особенности применительно к движению изощренное понимание мгновенной скорости он предложил культуре, где лишь недавно придумали способ измерять скорость: бросать прикрепленную к лагу веревку, на которой завязаны узлы, за корму и считать, сколько узлов ушло за борт за единицу времени. Впервые появился смысл в понятии скорости тела – или же в изменении чего угодно – в заданный момент времени.

Ныне математический анализ применяется для описания каких угодно изменений – обтекание крыльев самолета воздухом, рост населения, перемены в климатических системах, подъемы и падения биржевых показателей, ход химических реакций. В любом деле, где можно графически отразить количество, в любой области науки, математический анализ – ключевой инструмент[196].

Математический анализ позволил Ньютону соотнести приложенную к телу силу в любой момент времени с изменением скорости в этот же момент. Более того, постепенно прояснилось, как сложить все бесконечно малые изменения скорости и вывести из этого траекторию тела как функцию от времени. Но этим законам и методам пришлось подождать открытия еще несколько десятилетий.

И в физике, и в математике «Черновая книга» Ньютона превзошла все доселе вообразимое. До Ньютона, к примеру, столкновение тел воспринималось как состязание между внутренними устройствами этих тел, словно двое мускулистых гладиаторов пытаются вышвырнуть друг друга с арены. В видении Ньютона же каждое тело осмысляется лишь в понятиях воздействующего на них внешнего побудителя, сиречь силы.

Вопреки этому мыслительному прорыву, среди более чем сотни аксиом «Черновой книги», связанных с этой задачей, Ньютон дает лишь неполное и заковыристое определение того, что он понимает под «силой». Самое главное: он совсем не поясняет, как определять количественно силу, с коей, например, Земля притягивает тела, или ту, что «меняет движение» тела. Полотно, которое Ньютон принялся писать в Вулсторпские годы, останется незавершенным почти двадцать лет, и оно – лишь тень той искры, что потребовалась для ньютонианской революции.

 

* * *

 

Физик Джереми Бернстайн рассказывает историю посещения Соединенных Штатов австрийским физиком Вольфгангом Паули в 1958 году. Паули представил свою теорию публике Колумбийского университета, среди которой находился Нильс Бор, относившийся к соображениям Паули скептически. Паули согласился, что на первый взгляд его теория может казаться несколько безумной, однако Бор ответил, что нет, беда как раз в том, что теория недостаточно безумна. На что Паули, обращаясь к залу, возразил: «Нет, моя теория безумна достаточно!» Но Бор не унимался: «Нет, ваша теория не безумна в нужной мере!»[197]И вот уж двое знаменитых физиков ссорятся посреди зала и вопят, как пятиклашки.

Я вспомнил эту историю, дабы показать, что все физики – и все новаторы – предлагают гораздо больше ошибочных суждений, нежели верных, и, если физик – мастер своего дела, у него возникают и безумные соображения, которые как раз лучше всех – если, конечно, они верны. Отличить заблуждение от прозрения – дело не из легких, на него может уйти уйма времени и усилий. А значит, к людям с диковинными идеями следует относиться с пониманием. Ньютон был одним из них: столь бодро начав в период чумы, он затем провел значительную часть своей жизни, развивая ошибочные соображения, которые позднейшие ученые, изучавшие труды Ньютона, считали безумными.

Все начиналось неплохо. Весной 1667 года, вскоре после возобновления работы Кембриджа, Ньютон вернулся в Колледж Св. Троицы. Той осенью в колледже проходили выборы. Все мы временами оказываемся в обстоятельствах, оказывающих громадное влияние на наше будущее, – личные преодоления, собеседования, способные изменить всю нашу жизнь, экзамены в колледжи или профессиональные школы, чьи результаты могут сильно расширить наши дальнейшие возможности. Выборы в Колледже Св. Троицы оказались для Ньютона всем сразу: их результат определял, сможет ли двадцатичетырехлетний ученый остаться в университете на положении «соискателя», или же далее ему придется пасти овец и грести навоз. Шансы его были невелики: выборов в Колледже Троицы не происходило уже три года[198], мест было всего девять, а кандидатов гораздо больше, многие – с политическими связями. Некоторые даже располагали письмами с визой короля, с требованием принять подателя письма на свободное место. Но Ньютона все же выбрали.

Сельскохозяйственная карьера теперь прочно осталась в прошлом, и, казалось бы, Ньютону – полная воля взяться за дело и преобразовать записи из «Черновой книги» по математическому анализу и движению в законы Ньютона. Но нет. Следующие несколько лет Ньютон трудился в двух совершенно других областях – в оптике и математике, в особенности в алгебре. За последнее ему было щедро воздано: вскоре в небольшом сообществе кембриджских математиков его стали считать гением. В результате, когда влиятельный Исаак Барроу [Айзек Бэрроу] покинул почетный пост Лукасовского профессора математики – им несколько столетий спустя стал Стивен Хокинг, – он, по сути, устроил так, чтобы его место занял Ньютон[199]. Заработок по тем временам получался потрясающий: теперь университет был готов платить Ньютону в десять раз больше, чем выделяла ему мать – сто фунтов в год.

Усилия Ньютона, посвященные оптике, впрочем, принесли ему меньше славы. Еще студентом он прочел свежие труды по оптике и свету оксфордского ученого Роберта Бойля [Бойла] (1627–1691), который был еще и первопроходцем-химиком, и Роберта Гука (1635–1703), «скрюченного и бледнолицего» человека – хорошего теоретика и блестящего экспериментатора, как показала его работа ассистентом у Бойля. Труды Бойля и Гука вдохновили Ньютона, однако он так в этом и не признался. Но вскоре уже не просто занимался расчетами – он экспериментировал, вытачивал стекла и совершенствовал телескоп.

Ньютон взялся за изучение света под всевозможными углами[200]. Он вводил себе в глаз иглу и жал на него, пока не начинал видеть белые и цветные круги. Происходит ли свет от давления? Ньютон таращился на солнце, покуда хватало терпения – так долго, что потом несколько дней приходил в себя, – и отмечал, что, отводя взгляд от солнца, видел цвета искаженными. Свет существует на самом деле, или же это плод воображения?

Чтобы изучать свет лабораторно, Ньютон проделал дырочку в ставнях на единственном окне у себя в кабинете, чтобы свет проникал внутрь в виде луча. Такой свет, как думали ученые, белый чистейшего свойства, то есть совершенно бесцветный. Гук пропускал луч света через призмы и наблюдал, как из них струится цветной свет. Он заключил, что прозрачные вещества вроде призмы производят цвет. Но Ньютон тоже пропускал луч света через призмы и пришел к другому выводу. Он отметил, что призмы расщепляют белый свет на цвета, однако цветной свет не меняют. Наконец Ньютон заключил, что стекло не производит цвет, но, изгибая поток света по-разному для разных цветов, делит белый свет на цвета, из которых состоит. Белый свет не есть чистый цвет, а смесь цветов, объявил Ньютон.

Эти наблюдения привели Ньютона к теории цвета и света, над которой он трудился с 1666 по 1670 год. Результатом стал вывод – когда Гук назвал его «гипотезой», Ньютон рассвирепел, – что свет состоит из крошечных «корпускул», вроде атомов. Теперь-то мы знаем, что Ньютонова теория ошибочна в частностях. Действительно, представление о корпускулах света вернется к жизни через несколько веков, в работах Эйнштейна, и ныне мы называем эти корпускулы фотонами. Но фотоны Эйнштейна – квантовые частицы, и они в теорию Ньютона не укладываются.

Хотя работа Ньютона над усовершенствованием телескопа принесла ему славу, представление о световых корпускулах было воспринято во времена Ньютона, как это вышло и с Эйнштейном, с большим скепсисом. А в случае с Робертом Гуком, чья теория описывала свет состоящим из волн, – с неприятием. Более того, Гук жаловался, что Ньютон лишь слегка видоизменил его эксперименты, которые Гук поставил первым, и выдал их за свои.

Годы беспорядочного питания и бессонных ночей, проведенные в оптических исследованиях, привели Ньютона к интеллектуальному сражению, которое быстро сделалось озлобленным и жестоким. Что еще хуже, Гук был человеком порывистым и рубил с плеча – сочинял ответы Ньютону всего за пару часов, тогда как Ньютон, педантичный и тщательный во всем, ощущал нужду отвечать со всей прилежностью. На один такой ответ у него как-то раз ушло несколько месяцев.

Но да пусть ее, личную вражду: так состоялось знакомство Ньютона с публичной стороной нового научного метода – с открытым обсуждением и стычками идей. Ньютону не понравилось. Он, и без того склонный к уединению, из ученого общения устранился.

Заскучав от математики и разозлившись на критику своей оптики, к середине 1670-х Ньютон, к тому времени слегка за тридцать, но уже седой и обычно непричесанный, практически отрезал себя от всего научного сообщества. Отрезанным он и остался – на целый десяток лет.

Нетерпимость к противостояниям стала не единственной причиной его вновь обретенной почти полной изоляции: за предыдущие несколько лет, даже работая в математике и оптике, Ньютон начал уделять все больше времени своих сточасовых рабочих недель двум новым увлечениям, которые он не стремился ни с кем обсуждать. То были «безумные» исследовательские программы, за которые его с тех пор часто критикуют. И, конечно, они лежали сильно в стороне от столбовой дороги научных интересов: математический и текстовый анализ Библии – и алхимия.

Позднейшим исследователям решение Ньютона посвятить себя трудам по теологии и алхимии часто казалось непостижимым, словно он забросил писать статьи для журнала «Нейчер» и предпочел сочинять буклеты для сайентологов. Осуждение это, правда, не берет в расчет подлинного размаха затеи: задача, объединявшая усилия Ньютона в физике, теологии и алхимии, была одна и та же – постичь истину этого мира. Интересно всмотреться, хотя бы коротко, в эту работу – не потому, что она привела к верному ответу, и не потому, что доказывает, будто у Ньютона случались приступы сумасшествия, но потому что она делает зримой зачастую тонкую грань между научным поиском, который в итоге оказывается плодотворным, и бесплодными усилиями.

Ньютон верил обещаниям Библии, что истина будет явлена людям набожным, хотя некоторые стороны этой истины одним лишь чтением текстов не увидеть. Верил он и в то, что набожные люди прошлого, включая великих алхимиков вроде швейцарского врача Парацельса, обрели важные прозрения и включили их в свои работы в зашифрованном виде – чтобы скрыть от неверных. Выведя закон всемирного тяготения[201], Ньютон уверился, что Моисей, Пифагор и Платон постигали этот закон задолго до него.

Что Ньютон превратил свои замыслы в математический анализ Библии, понять можно – с его-то талантами. В ходе работы он обратил внимание на точные даты Творения, постройки Ноева Ковчега и других библейских событий. На основании библейских текстов он рассчитал и неоднократно пересмотрел предсказания конца света[202]. В одной из последних версий мир придет к своему концу где-то между 2060 и 2344 годами. (Не могу сказать, окажется ли это правдой, но, как ни странно, это предсказание точно совпадает с некоторыми сценариями глобальной перемены климата.)

Вдобавок Ньютон усомнился в подлинности многих фрагментов текста Библии и пришел заключению, что имел место впечатляющий подлог, исказивший наследие ранней Церкви в пользу представления о Христе как о Боге, что Ньютон считал идолопоклонничеством. Вкратце: Ньютон не верил в Святую Троицу, что в его положении профессора Колледжа Троицы может показаться забавным. Придерживаться таких взглядов было опасно: Ньютон мог запросто потерять и свое положение, и, вероятно, кое-что посерьезнее, узнай о его воззрениях кто-нибудь неподходящий. Но Ньютон, разбираясь в христианстве, был в отношении публичности своих работ крайне осмотрителен: невзирая на то, что эти труды посвящались религии, а не революции в науке, Ньютон считал их наиболее важными.

Вторая страсть Ньютона в те годы, алхимия, тоже поглощала колоссальные время и силы, и эти исследования продолжались тридцать лет – куда больше, чем он когда-либо посвящал физике. Денег они тоже требовали немало: Ньютон не только оснащал себе алхимическую лабораторию, но и собирал библиотеку. Здесь тоже легко пренебречь этими его исканиями как ненаучными – и ошибиться: как и прочие свои исследования, алхимические Ньютон проводил с тем же тщанием и, с учетом его глубинных взглядов, с той же добротной аргументацией. В этой области Ньютон также пришел к выводам, которые нам трудно понять, поскольку рассуждения его укоренены в контексте, для нас совершенно незнакомом.

Ныне мы представляем себе алхимиков бородатыми мужчинами в мантиях, произносившими заклинания в попытках превратить мускатный орех в золото. Конечно, первый известный нам алхимик – египтянин по имени Болос из Мендеса, живший около 200 года до н. э., который завершал каждый «эксперимент» заклинанием: «Одна сущность в другой утешается. Одна сущность другой истребляется. Одна сущность другой подчиняется»[203]. Смахивает на перечисление возможных событий в брачном союзе двоих людей. Но сущности, о которых говорил Болос, – химические вещества, и Болос в химических реакциях явно кое-что смыслил. Ньютон верил, что в далеком прошлом ученые, подобные Болосу, открыли глубинные истины, с тех пор утерянные, но восстановимые путем анализа греческих мифов, кои, по убеждению Ньютона, не что иное как зашифрованные алхимические рецепты.

В своих алхимических изысканиях Ньютон, сохраняя тщательность научного подхода, провел великое множество продуманных экспериментов с подробнейшими описаниями. Будущий автор «Принципов», часто именуемых величайшей книгой в истории науки, провел многие годы, исписывая тетради лабораторными наблюдениями вроде вот таких: «Растворить летучего зеленого льва в центральной соли Венеры, перегнать. Полученный спирит есть зеленый лев кровь зеленого льва Венеры, Вавилонский Дракон, убивающий все своим ядом, но, побежденный смягчением Горлиц Дианы, есть Узы Меркурия»[204].

Начиная карьеру в науке, я поклонялся ее героям, Ньютонам и Эйнштейнам – и историческим, и современным гениям вроде Фейнмана. Вступать в поле, на котором родились все эти великие, – дело для юного ученого требовательное. Я ощутил это давление величия, когда получил место в Калтехе[205]. Похоже я себя чувствовал накануне первого дня в старшей школе, когда боялся идти на занятие по физкультуре и особенно мыться потом в ду́ше на глазах у других пацанов. В теоретической физике оголяешься – не физически, но интеллектуально, и все на тебя смотрят – и выносят суждения.

Об этих неуверенностях редко говорят, ими редко делятся, и все же они обычны. Любому физику приходится искать собственный способ преодолевать это напряжение, но, чтобы достичь успеха, одного последствия следует избегать каждому: боязни ошибиться. Томасу Эдисону часто приписывают совет: «Чтобы вышел отличный замысел, плодите их обильно». И, разумеется, любой новатор проходит гораздо больше тупиков, нежели достославных бульваров, и потому бояться ошибиться поворотом означает наверняка никогда не прийти в какое-нибудь интересное место. И потому я в те свои времена был бы рад услышать обо всех Ньютоновых заблуждениях и впустую потраченных годах.

Тем, кому утешительно знать, что люди блистательно правые тоже иногда ошибаются, сообщаем: даже гений, подобный Ньютону, может заблуждаться. Да, он догадался, что тепло есть результат движения крошечных частиц, из которых, как он считал, состоит вся материя, но он же, подумав, что заболел туберкулезом, прописал себе «лекарство» из скипидара, розовой воды, пчелиного воска и оливкового масла. (Это снадобье считалось целительным и при болезнях грудей, и от укуса бешеной собаки.) Да, он изобрел математический анализ, но полагал, что поэтажный план затерянного храма царя Соломона в Иерусалиме скрывает математические подсказки касательно конца света.

Почему Ньютон так сильно отклонился от курса? Если присмотреться к обстоятельствам жизни ученого, один фактор бросается в глаза: его обособленность. В точности так же, как интеллектуальная обособленность привела к скверному положению в науке в средневековом арабском мире, она же, судя по всему, препятствовала и Ньютону, хотя в его случае уединение он предпочел для себя сам, поскольку свои религиозные и алхимические взгляды держал при себе, не желая подвергаться риску осмеяния или даже запретов, какие могли возникнуть, откройся он для интеллектуального обсуждения. Не было «хорошего» и «плохого» Ньютона[206], рационального и иррационального, писал оксфордский философ У. Х. Ньютон-Смит. Ньютон заблуждался, потому что не открыл свои взгляды для обсуждения и критики «общественному форуму», а это – одна из важнейших «норм института науки».

Ньютон, на дух не выносивший критики, в той же мере не торопился делиться своими революционными исследованиями, которые проводил в области

физики движения в чумные годы. Пробыв на посту Лукасовского профессора пятнадцать лет, он все еще не опубликовал и не закончил эту свою работу. В итоге в 1684 году, когда ему уже был сорок один, этот маниакально прилежный гений имел на руках лишь ворох разрозненных заметок и статей по алхимии и религии, труд, состоявший из неоконченных математических выкладок, и теорию движения, все еще путаную и неполную. Ньютон произвел подробнейшие исследования в нескольких областях, но не пришел ни к какому твердому выводу, оставив свои соображения в математике и физике в состоянии, подобном пересыщенным солевым растворам, – переполненными содержанием, но не кристаллизовавшимися.

Вот к чему пришел в те годы Ньютон. Историк Уэстфолл говорит: «Умри Ньютон в 1684 году и оставь по себе свои записи, о существовании этого гения мы бы узнали из них. Но не славили бы его как человека, придавшего форму современному интеллекту, а в лучшем случае поминали парой абзацев, скорбя по его неспособности довести замыслы до полноты воплощения»[207].

Что судьба Ньютона сложилась иначе – заслуга не сознательного решения ученого закончить и издать свой труд. Напротив, в 1684 году ход научной истории изменила почти случайная встреча, разговор с коллегой, подарившим необходимые соображения и стимулы, которых Ньютону не хватало. Не будь этой встречи, история науки, да и нынешний мир, были бы совсем другими – и вряд ли лучше.

 

* * *

 

Семя, выросшее в величайшее достижение науки из всех, какие видел мир, проросло после встречи Ньютона с коллегой, заезжавшим в Кембридж жарким поздним летом.

В январе того судьбоносного года астроном Эдмунд Галлей – тот самый, имени которого комета, – присутствовал на заседании Королевского общества в Лондоне, влиятельного ученого сообщества, посвященного науке, где обсуждал с двумя своими коллегами горячую тему дня. Несколькими десятилетиями ранее, применив данные невероятной точности, собранные датским аристократом Тихо Браге [Тио Бра] (1546–1601), Иоганн [Йоханнес] Кеплер открыл три закона, описывающие, похоже, орбиты планет. Он заявил, что орбиты планет эллиптичны, что Солнце размещается в одном из двух фокусов эллипса, и сформулировал определенные правила, которым эти орбиты подчиняются: к примеру, что квадрат времени, потребный для совершения полного цикла по орбите, пропорционален кубу среднего расстояния до Солнца. В некотором смысле эти законы – красивые и компактные описания того, как планеты движутся в пространстве, однако в ином смысле – порожние наблюдения, случайно совпавшие утверждения, не проливавшие никакого света на то, почему именно по таким орбитам движутся планеты.

Галлей и двое его коллег заподозрили, что законы Кеплера отражают некую глубинную истину. В частности, они предположили, что все законы Кеплера вытекают из допущения, что Солнце притягивает к себе любую планету с силой, ослабевающей пропорционально квадрату расстояния до этой планеты, то есть в согласии с математической формулировкой, именуемой «законом обратных квадратов».

То, что сила, исходящая во все стороны от удаленного тела, подобного Солнцу, должна уменьшаться пропорционально квадрату расстояния от этого тела, можно доказать геометрически. Вообразите исполинскую сферу – до того большую, что Солнце будет всего лишь точкой в центре. Все точки поверхности этой сферы равноудалены от Солнца, следовательно, в отсутствие других причин считать иначе, можно предположить, что физическое влияние Солнца – по сути, «силовое поле» – должно быть распределено равномерно по всей поверхности сферы.

Теперь представим сферу, скажем, вдвое больше. Законы геометрии говорят нам, что увеличение радиуса сферы вдвое дает вчетверо большую поверхность, а значит, теперь сила притяжения солнца будет распределена по поверхности в четыре раза большей. В таком случае разумно считать, что в любой точке большей сферы притяжение Солнца составит одну четвертую от значения для исходной сферы. Вот так работает закон обратных квадратов: чем дальше от источника силы, тем слабее притяжение – в обратной пропорции к квадрату расстояния.

Галлей и его коллеги предположили, что за законами Кеплера стоит закон обратных квадратов, но могли ли они это доказать? Один, Роберт Гук, сказал, что может. Второй, Кристофер Рен, которого мы ныне лучше всего знаем по архитектурным работам, был в те времена еще и известным астрономом, и он предложил Гуку награду в обмен на доказательство. Гук отказался. Он был знаменит противоречивостью, но объявленные им основания отказа выглядели сомнительно: он сказал, что не раскроет доказательства, чтобы другие, не сумев с ним справиться, оценили всю сложность задачи. Быть может, Гук и впрямь справился. Быть может, он и дирижабль, на котором можно долететь до Венеры, изобрел. В любом случае доказательства он так никогда никому и не показал.

Через семь месяцев после того разговора Галлей, оказавшись в Кембридже, решил заглянуть к профессору-отшельнику Ньютону. Как и Гук, Ньютон сказал, что проделал работу, доказывающую предположение Галлея. Как и Гук, он его не предъявил. Порылся в каких-то бумагах, доказательства не нашел, но пообещал еще поискать и погодя Галлею прислать. Прошло несколько месяцев, но Галлей так ничего не получил. Интересно, что он себе думал. Вот просит он двух умных взрослых людей решить задачку, один говорит: «Ответ знаю, но не скажу!», а второй, по сути: «Мою домашку съела собака». Награда по-прежнему оставалась у Рена.

Ньютон все же откопал доказательство, однако, всмотревшись в него еще раз, обнаружил ошибку. Однако не сдался – он переработал свои соображения и в конце концов добился успеха. Тем ноябрем он отправил Галлею трактат на девяти страницах, доказывающий, что все три закона Кеплера – действительно математические следствия закона обратных квадратов. Он назвал свой краткий труд «De Motu Corporum in Gyrum» («О движении тел по орбите»).

Галлей пришел в восторг. Он увидел в подходе Ньютона революцию и захотел, чтобы Королевское общество опубликовало эту работу. Однако Ньютон отклонил предложение. «Я занялся этим предметом, – сказал он, – и рад был бы разобраться до основания и лишь потом издавать свои записи»[208]. Ньютон «рад был бы разобраться»? То, что далее последовало, превратилось в титанический подвиг, приведший, быть может, к самому значительному интеллектуальному прозрению за всю историю, а сказанные в начале этого похода слова – самое грандиозное в истории преуменьшение значимости. Ньютон разберется с этой задачей «до основания», доказав, что фундаментальная основа устройства планетарных орбит – всеобщая теория движения и силы, применимая к любым телам, и небесным, и земным.

В последующие полтора года Ньютон занимался исключительно составлением трактата, который превратится в «Математические принципы». Он сделался машиной физики. Он всегда, чем-нибудь увлекшись, забывал о еде и даже о сне. Говорят, его кот растолстел, доедая пищу, которую Ньютон оставлял недоеденной на подносе, а старый сосед по жилищу в колледже сообщал, что нередко заставал Ньютона утром на том же месте, что и накануне вечером: великий затворник продолжал работать над той же задачей. Но на сей раз Ньютон пошел еще дальше. Он отказался от практически всех человеческих связей. Редко покидал комнату, а когда изредка все же наведывался в трапезную колледжа, перекусывал быстро и немного, стоя, после чего стремительно возвращался к себе.

Наконец-то Ньютон закрыл свою алхимическую лабораторию и отложил теологические изыскания. Лекции он читать продолжал, раз требовалось, однако получались они до странности смутные и путаные. Позднее стало понятно почему: Ньютон попросту являлся на занятия и читал черновики «Принципов».

 

* * *

 

Пусть Ньютон несколько десятков лет после получения должности в Колледже Св. Троицы не мог довести работу о силе и движении до конца, но в 1680-х он располагал куда более мощным интеллектом, нежели был у него в чумные 1660-е. Он теперь оказался гораздо лучше математически подготовлен, а благодаря занятиям алхимией имел и научный опыт. Некоторые историки даже считают, что именно годы занятий алхимией сделали возможным прорыв в изучении движения и написание «Принципов».

Парадокс: одним из катализаторов Ньютонова прорыва стало письмо, которое, как он вспоминал, он получил пятью годами ранее – от Роберта Гука. Тот предложил смотреть на движение по орбите как на сумму двух разных воздействий. Рассмотрим тело (например, планету), обращающееся по круговой орбите вокруг некоего другого тела, притягивающего его (как Солнце). Предположим, что обращающееся тело имеет склонность продолжать движение по прямой – то есть слететь с круговой орбиты и понестись дальше, как автомобиль, водитель которого не вписался в поворот на мокрой трассе. Математики называют это движением по касательной, или тангенциальным.

Теперь допустим, что у тела есть вторая склонность – притяжение к центру орбиты. Математики называют это движение нормальным, или центростремительным. Склонность к центростремительному движению, писал Гук, может быть дополняющим к тангенциальному, и тогда вместе они обеспечивают движение по орбите.

Легко понять, как это соображение отозвалось в Ньютоне. Вспомним, что, совершенствуя закон инерции Галилея, Ньютон предположил у себя в «Черновой книге», что все тела склонны продолжать движение по прямой, если нет внешнего воздействия на них, то есть силы. Для тела на орбите первая склонность – слететь с орбиты по прямой – естественно вытекает из этого закона. Ньютон понял, что, если добавить в эту картину силу, притягивающую тело к центру орбиты, возникнет причина центростремительного движения – второй необходимой составляющей, предложенной Гуком.

Но как это описать математически и, в особенности, как установить связь между конкретной формулой закона обратных квадратов и конкретными математическими свойствами орбит, описанными Кеплером?

Мысленно поделим время на крошечные интервалы. В каждом интервале времени тело, движущееся по орбите, можно представить себе движущимся по касательной на очень маленькие расстояния и в то же время центростремительно – тоже понемножку. Сумма этих движений возвращает тело на орбиту, но чуточку дальше вдоль окружности, чем вначале. Повторив эту последовательность много раз, получим зубчатую круговую орбиту, как показано на рисунке.

 

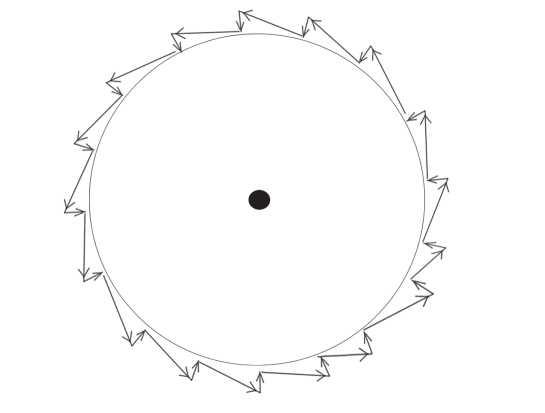
Круговое движение, возникающее из движения по касательной (тангенциального) и центростремительного (нормального).

 

Если на такой орбите взять достаточно малые промежутки времени, траектория будет совпадать с окружностью сколь угодно плотно. И вот тут пригодились наработки Ньютона в математическом анализе: если интервалы бесконечно малы, траектория в данном конкретном случае и есть окружность.

Таково описание орбит, какое позволила составить новая математика Ньютона. Он сложил вместе изображение тангенциального движения тела по орбите и нормального «падения», получилась зубчатая траектория – а затем взял предельный случай такого движения, в котором линейные сегменты сделались исчезающе малы. Таким образом зубчатость изгладилась до окружности.

Орбитальное движение в таком варианте есть движение любого тела, которое постоянно отклоняется от движения по касательной под действием силы, тянущей его к некоему центру. Дело в шляпе: применив закон обратных квадратов для описания центростремительной силы в математике орбит, Ньютон воспроизвел три закона Кеплера, как и просил Галлей.

Доказательство, что свободное падение и движение по орбите суть два проявления одних и тех же законов силы и движения, – один из величайших триумфов Ньютона, поскольку это раз и навсегда опровергло заявление Аристотеля, что небеса и Земля – разные «царства». Астрономические наблюдения Галилея выявили, что другие планеты очень похожи на Землю, работа Ньютона же доказала, что законы природы применимы и к другим планетам, а не только к Земле.

Но даже в 1684 году, тем не менее, Ньютоново понимание силы тяготения и движения не были внезапными всплесками ясности, на какие намекает история с падающим яблоком. Напротив, революционная мысль[209]о том, что сила тяготения – всемирна, дошла до Ньютона, похоже, постепенно, пока он дорабатывал черновики «Принципов».

Прежде ученые, если и подозревали, что у планет есть сила тяготения, считали, что это тяготение воздействует только на их луны, но не на другие планеты, словно каждая планета – отдельный замкнутый мир со своими законами. Ньютон и сам поначалу разбирался лишь с тем, распространяется ли причина падения тел к Земле на притяжение Луны Землей, но не с притяжением планет Солнцем.

Следует признать творческую силу Ньютона, незашоренность его мысли: он усомнился в привычном мировоззрении. Он написал одному английскому астроному и запросил даты движения комет в 1680 и 1684 годах, а также орбитальные скорости Юпитера и Сатурна в момент их сближения. Произведя изнурительные расчеты по присланным очень точным данным и сравнив результаты, Ньютон удостоверился, что одни и те же законы тяготения применимы повсюду – на Земле и меж небесных тел. Он внес это замечание в текст «Принципов».

Мощь законов Ньютона – не только в их революционном понятийном содержимом. Применяя их, он смог получать предсказательные результаты с неслыханной доселе точностью и сравнивать их с экспериментально полученными. К примеру, применив данные о расстоянии до Луны и радиусе Земли и приняв во внимание такие мелочи, как искажение лунной орбиты из-за притяжения Солнца, центробежную силу вращения Земли и отклонение формы Земли от идеального шара, Ньютон заключил, что на широте Парижа тело, брошенное из положения покоя, пролетит за первую секунду пятнадцать футов и одну восьмую дюйма[210]. Это, сообщил неизменно дотошный Ньютон, соответствует эксперименту с точностью до одной трехтысячной доли[211]. Более того, он кропотливо повторил эксперимент с разными материалами – золотом, серебром, свинцом, стеклом, песком, солью, водой, деревом и пшеном. Любое тело, пришел он к выводу, независимо от своего устройства, хоть на Земле, хоть на небесах, притягивает любое другое тело, и притяжение это всегда подчиняется одним и тем же законам.

 

* * *

 

Когда Ньютон «добрался до основания» начатого, работа «О движении тел по орбите» распухла с девяти страниц до трех томов – до «Принципов», а точнее – «Математических принципов натуральной философии».

«Принципы» Ньютон посвятил не исключительно движению тел по орбите – он подробно излагал теорию силы и движения как таковую. Суть движения – взаимосвязь трех количественных параметров: силы, импульса (который Ньютон называл количеством движения) и массы.

Мы уже знаем, как Ньютон силился сформулировать свои законы. Теперь давайте посмотрим на сами законы и разберемся в их значении. Первый – уточнение Галилеева закона инерции, но с важным дополнительным утверждением, что сила есть причина изменений:

Первый закон Ньютона: Всякое тело продолжает оставаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

Ньютон, как и Галилей, определяет движение, при котором тело перемещается по прямой с постоянной скоростью, как естественное положение дел. Поскольку ныне мы склонны думать в ньютоновских понятиях, оценить, до чего неочевидно это представление, затруднительно. Но движение, которое мы наблюдаем вокруг, в основном не происходит по Ньютонову описанию: предметы, падая, ускоряются или же замедляются сопротивлением воздуха – или движутся по искривленным траекториям, перемещаясь к земле. Ньютон считал, что эти виды движения – в некотором смысле отклонения от нормального, результат действия незримых сил вроде гравитации или трения. Если предоставить тело самому себе, говорил он, оно будет двигаться равномерно, а если траектория движения искривляется, или же меняется скорость, это происходит под действием внешних сил.

Факт, что тела, предоставленные себе, продолжают сохранять свое состояние движения, позволяет нам исследовать космос. На Земле «феррари», к примеру, может разогнаться с нуля до шестидесяти миль в час менее чем за четыре секунды, однако, чтобы сохранять эту скорость, автомобилю приходится изрядно стараться – из-за сопротивления воздуха и трения. Средство перемещения в открытом космосе сталкивается с одной случайной молекулой примерно раз в сто тысяч миль, и потому о трении или торможении можно не беспокоиться. Это означает, что достаточно разогнать космическое судно, и оно продолжит двигаться по прямой с постоянной скоростью без замедления, в отличие от «феррари». А если не выключать двигатели, можно продолжать разгоняться, не теряя при этом энергии на трении. Если, скажем, ваш космический корабль разгоняется со скоростью «феррари», и разгон продолжится год, а не секунду, удастся достичь половинной скорости света.

Есть, конечно, кое-какие практические трудности – масса топлива, которую придется везти с собой, а также эффекты относительности, до которых мы еще доберемся. Кроме того, если хотите долететь до какой-нибудь звезды, придется хорошенько прицелиться: звездные системы до того разрежены, что, если нацелить корабль «от балды», прежде чем достичь какой-нибудь другой солнечной системы, он в среднем улетит дальше, чем удалось свету со времен Большого взрыва.

Ньютон не воображал визиты человека на другие планеты, однако, постановив, что сила придает телу ускорения, во втором законе он количественно определяет связь между количеством силы, массой и ускорением (в современных понятиях «изменение количества движения» означает смену импульса, то есть равно массе, умноженной на ускорение):

Второй закон Ньютона: Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Представьте, что толкаете тележку с ребенком в ней. Закон утверждает: если, не учитывая трения, толкнуть 75 фунтов тележки с ребенком так, чтобы она разогналась до пяти миль в час, то на разгон 150-фунтовой тележки с подростком до той же скорости пришлось бы затратить вдвое больше усилий – или же толкать вдвое дольше. Вот что хорошо (опять-таки, без учета трения): можно разогнать 750 000-фунтовый аэробус до скорости пять миль в час, толкая его в 10 000 раз сильнее, что трудно, или в 10 000 раз дольше, а это просто требует терпения. Поэтому, если вы готовы прилагать равномерные усилия 10 000 секунд – а это не так долго, всего-то два часа сорок семь минут – могли бы покатать целый аэробус пассажиров.

В наши дни мы записываем второй закон Ньютона так: F = та, то есть сила равно масса, умноженная на ускорение, однако второй закон принял вид уравнения много позже, уже после смерти Ньютона и через сто лет после того, как Ньютон этот закон сформулировал.

В третьем законе Ньютон утверждает, что общее количество движения во Вселенной не меняется. Оно может передаваться от тела к телу, но его ни отнять, ни прибавить. Суммарное количество движения, наличное во Вселенной, было от ее рождения и останется неизменным, пока существует Вселенная.

Важно отметить: согласно формулировке Ньютона, количество движения в одном направлении, сложенное с соответствующим движением в противоположном направлении, дает сумму движения, равную нулю. Таким образом, тело можно перевести из состояния покоя в движение, не нарушая третий закон Ньютона, если это движение скомпенсировано изменением движения второго тела в противоположном направлении. Ньютон формулирует это так:

Третий закон Ньютона: Действию всегда есть равное и противоположное противодействие.

Эта невинная с виду фраза сообщает нам, что, если пуля летит вперед, ружье сдает назад. Если конькобежка отталкивается ото льда лезвием конька, сама она поедет вперед. Если вы чихнете, исторгая воздух изо рта вперед, голова у вас откинется назад (со средним ускорением, втрое превышающим ускорение свободного падения, как сообщает нам журнал «Спайн»)[212]. А если космический корабль выбрасывает горячие газы из сопла, сам он ускоряется с импульсом, равным по величине, но противоположным относительно движения горячих газов, вытолкнутых в космический вакуум.

Законы Ньютона, представленные в «Принципах», не были просто абстракциями. Ньютон смог убедительно доказать, что этой малостью математических принципов можно описать бессчетное множество явлений действительности. Вот некоторые практические приложения: он показал, что сила тяготения создает наблюдаемые неравномерности в движении Луны; объяснил морские приливы; рассчитал скорость звука в воздухе; показал, что предварение равноденствий[213]– воздействие гравитационного притяжения Луны на экваториальную выпуклость Земли.

То были поразительные достижения, и мир, конечно, поразился. Но в некотором смысле еще больше потрясает, что Ньютон понимал: у его законов есть практические пределы применимости. Он, к примеру, знал, что, хотя его законы движения – в целом, отличное приближение наблюдаемого вокруг нас, они истинны в абсолютном смысле лишь в идеальном мире, где нет ни сопротивления воздуха, ни трения.

 

 

Величие гения Ньютона, как и Галилея, еще и в том, что он осознавал множес