|
|
Приборы и оборудование
Генератор с индикацией частоты (самодельный), исследуемые образцы.
Выполнение работы
Измерительная катушка генератора намотана на полый цилиндрический каркас, внутрь которого помещается пробирка с исследуемым образцом. При помещении магнетика внутрь катушки изменяется эффективная магнитная проницаемость внутри объёма катушки, что приводит к изменению её индуктивности и частоты генерации. Изменение частоты генерации позволяет (с учетом коэффициента заполнения) определить магнитную восприимчивость образца.
Ход выполнения работы:
- Включить измерительный прибор (генератор) в сеть и дать ему прогреться;
- Зная материалы образцов и их массы (при необходимости взвесить) вычислить объемы;
- Записать частоту генерации без образца;
- Поместить один из образцов (внутри пробирки) внутрь катушки генератора. Записать частоту генерации с образцом;
- Повторить пункт 4 для остальных образцов;
- Вычислить магнитную восприимчивость образцов χ (с учетом коэффициента заполнения) и сравнить их с табличными значениями.
Контрольные вопросы: Какие вещества являются магнетиками. Типы магнетиков. Качественно объяснить поведение различных типов магнетиков с точки зрения строения атомов. Что такое магнитная восприимчивость. Вывести формулу для магнитной восприимчивости диа- и парамагнетиков. Температурная зависимость магнитной восприимчивости парамагнетиков.
Лабораторная работа №4
Определение магнитной проницаемости ферритов
Цель работы: Измерить индуктивность катушки на ферритовом кольце и рассчитать магнитную проницаемость. [1], [2], [6], [8].
Введение
§2.1. Ферромагнитный порядок.
Любой ферромагнетик обладает спонтанным магнитным моментом (внутри домена), то есть обладает конечной намагниченностью даже при нулевом внешнем магнитном поле. Это означает, что электронные спины и магнитные моменты ориентированы в веществе упорядоченным образом. Возможные типы упорядочения электронных спинов:
 |  |  |  |
1). Простой ферромагнетик.
 |  | ||||||
 |  | ||||||
2). Антиферромагнетик.
 |
3). Ферримагнетик (феррит)
 |  | ||||||
 |  | ||||||
4). Антиферромагнетик со спинами расположенными под углом
друг к другу.
 | |||||
 |  | ||||
5). Гелиоидальное распределение спинов.
Точка Кюри и обменный интеграл.
Рассмотрим парамагнетик с концентрацией 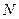 в единице объема со спином
в единице объема со спином  . Если существующие в кристалле взаимодействия стремятся расположить магнитные моменты параллельно друг к другу, то это ферромагнетик. Пусть в ферромагнетике существует такое взаимодействие, что его можно описать некоторым эффективным магнитным полем (молекулярное, обменное). Ориентирующему эффекту этого поля противостоит дезориентирующее влияние теплового движения. При повышении температуры в какой-то момент тепловое движение разрушает спиновое упорядочение и ферромагнетик переходит в парамагнетик.
. Если существующие в кристалле взаимодействия стремятся расположить магнитные моменты параллельно друг к другу, то это ферромагнетик. Пусть в ферромагнетике существует такое взаимодействие, что его можно описать некоторым эффективным магнитным полем (молекулярное, обменное). Ориентирующему эффекту этого поля противостоит дезориентирующее влияние теплового движения. При повышении температуры в какой-то момент тепловое движение разрушает спиновое упорядочение и ферромагнетик переходит в парамагнетик.
Пусть обменное поле  , эквивалентно по ориентирующему эффекту. Пусть
, эквивалентно по ориентирующему эффекту. Пусть  пропорционально намагниченности. Если есть домены, то
пропорционально намагниченности. Если есть домены, то  значение намагниченности в домене. В приближении усредненного поля считается, что каждый магнитный атом испытывает действие
значение намагниченности в домене. В приближении усредненного поля считается, что каждый магнитный атом испытывает действие  пропорционального намагниченности.
пропорционального намагниченности.

 (2.1)
(2.1)


Согласно (2.1) каждый спин подвергается воздействию всех других спинов. И это воздействие характеризуется средней намагниченностью.
Точка Кюри  определяется как температура, выше которой самопроизвольная намагниченность исчезает.
определяется как температура, выше которой самопроизвольная намагниченность исчезает.
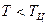 ферромагнитная фаза.
ферромагнитная фаза.
 парамагнитная фаза.
парамагнитная фаза.
 Рассмотрим парамагнитную фазу.
Рассмотрим парамагнитную фазу. 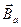 создает конечную намагниченность, которая создает конечное обменное поле
создает конечную намагниченность, которая создает конечное обменное поле  .
.
|
 (СИ)
(СИ)
 (СГС)
(СГС)


 (2.3)
(2.3)
При 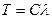 восприимчивость имеет особенность. При этой и более низких температурах существует спонтанная намагниченность.
восприимчивость имеет особенность. При этой и более низких температурах существует спонтанная намагниченность.
Закон Кюри – Вейса: 
 (2.4)
(2.4)
Этот закон хорошо описывает зависимость 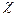 от
от 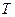 в парамагнитной фазе.
в парамагнитной фазе.


 (2.5)
(2.5)
 поля всех спинов решетки.
поля всех спинов решетки.
Обменное поле дает примерное представление о величине сил квантовомеханического обменного взаимодействия.
Выражение для энергии взаимодействия атомов  и
и  , обладающих спинами
, обладающих спинами  и
и  :
:

 (2.6)
(2.6)
 обменный интеграл, величина которого зависит от степени перекрытия распределения зарядов атомов
обменный интеграл, величина которого зависит от степени перекрытия распределения зарядов атомов  и
и  .
.
Модель ферромагнетика, в которой исходят из выражения для энергии вида (2.6) называется моделью Гейзенберга.
Распределение зарядов в системе из двух электронов зависит от расположения их спинов, что связанно с принципом Паули. Таким образом электростатическая энергия  системы зависит от относительной ориентации спинов. Разность энергий, отвечающих двум этим ориентациям, определяет обменную энергию.
системы зависит от относительной ориентации спинов. Разность энергий, отвечающих двум этим ориентациям, определяет обменную энергию.
Пусть атом имеет  ближайших соседей, и взаимодействие каждого из них с центральным атомом характеризуется величиной
ближайших соседей, и взаимодействие каждого из них с центральным атомом характеризуется величиной  . Пусть для более далеких атомов
. Пусть для более далеких атомов  . Энергия
. Энергия  , требуемая для переворачивания спина в присутствии всех других спинов:
, требуемая для переворачивания спина в присутствии всех других спинов:

 (2.7)
(2.7)
 среднее значение спина в направлении намагниченности.
среднее значение спина в направлении намагниченности.
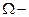 объем, приходящийся на один атом.
объем, приходящийся на один атом.
Средний магнитный момент электрона обусловлен спином.
 – намагниченность насыщения.
– намагниченность насыщения.

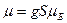 .
.

 (2.8)
(2.8)
 (2.9)
(2.9)
Температурная зависимость намагниченности насыщения.
 Будем искать намагниченность ниже температуры Кюри. Воспользуемся приближением усредненного поля в виде функции Бесселя. Пусть есть спин
Будем искать намагниченность ниже температуры Кюри. Воспользуемся приближением усредненного поля в виде функции Бесселя. Пусть есть спин  , магнитный момент
, магнитный момент 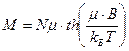 , где
, где  внешнее поле,
внешнее поле,  .
.
 (2.10)
(2.10)
Решение этого уравнения при  существует только при
существует только при  но
но  .
.
Пусть  – приведенная намагниченность,
– приведенная намагниченность,  – приведенная температура.
– приведенная температура.

 (2.11)
(2.11)
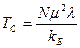
При увеличении температуры намагниченность плавно уменьшается и обращается в ноль при  . Такое поведение намагниченности позволяет считать такой переход из ферромагнитного состояния в парамагнитное и обратно фазовым переходом 2-го рода.
. Такое поведение намагниченности позволяет считать такой переход из ферромагнитного состояния в парамагнитное и обратно фазовым переходом 2-го рода.
Фазовый переход 1-го рода:  , изменяется энтропия и объем.
, изменяется энтропия и объем.
Фазовый переход 2-го рода: нет выделения или поглощения теплоты и изменения объема и энтропии, но скачкообразно изменяется теплоемкость, что связанно с изменением симметрии.
Теория усредненного поля плохо описывает ход изменения намагниченности при  .
.
Спиновые волны.
В основном состоянии простого ферромагнетика все спины параллельны. Рассмотрим 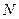 спинов
спинов
|
 |

 (2.12)
(2.12)
 спиновый момент количества движения электрона в узле с номером
спиновый момент количества движения электрона в узле с номером  , пусть
, пусть  классические вектора
классические вектора 

|





Возбуждение значительно меньшей энергии можно образовать, если допустить, что все спины повернулись лишь частично.
 |  |  | |||||
| |||||||
то «магнонами».
 |  |  |  |  | |||||||||||
 |  | ||||||||||||||
 |
Магноны сходны с колебаниями решетки (фононами) и представляют собой колебания относительной ориентации спинов в решетке.
Выведем дисперсионный закон для магнонов:
Из (2.12) выпишем отдельные члены, содержащие спины с номером  :
:

 (2.16 а)
(2.16 а)
 Для магнитного момента в узле
Для магнитного момента в узле  :
:  (2.16 б)
(2.16 б)

 (2.16 в)
(2.16 в)
 или
или  (2.16 г)
(2.16 г)
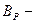 эффективное магнитное поле – обменное поле, действующее на спин
эффективное магнитное поле – обменное поле, действующее на спин  .
.

 (2.17)
(2.17)

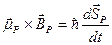 (2.18)
(2.18)
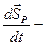 скорость изменения момента количества движения.
скорость изменения момента количества движения.

 (2.19)
(2.19)
 Или в проекциях:
Или в проекциях:
 (2.20)
(2.20)
Если амплитуда возбуждения мала, то, считая все проекции  (на
(на  ) равными
) равными 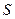 и пренебрегая членами
и пренебрегая членами  и
и 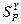 в уравнении для изменения
в уравнении для изменения  со временем, получим:
со временем, получим:

 (2.21)
(2.21)

 (2.22)
(2.22)
Ищем решение в виде бегущих волн:

 (2.23)
(2.23)
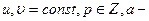 постоянная решетки.
постоянная решетки.
|

 (2.24)
(2.24)
|
| |
|
|


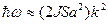 (2.25)
(2.25)
 определяется из опытов по спин – волновому резонансу в тонких пленках.
определяется из опытов по спин – волновому резонансу в тонких пленках.
Квантование спиновых волн.
Значение полного спинового квантового числа системы 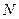 спинов величиной
спинов величиной 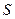 : равные значениям
: равные значениям 
В основном состоянии ферромагнетика полное спиновое число имеет величину 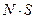 (в основном состоянии все спины параллельны).
(в основном состоянии все спины параллельны).
 Возбуждение спиновой волны уменьшает величину полного спина, так как спины становятся не параллельными. Найдем соотношение между амплитудой спиновой волны и величиной уменьшения
Возбуждение спиновой волны уменьшает величину полного спина, так как спины становятся не параллельными. Найдем соотношение между амплитудой спиновой волны и величиной уменьшения  компоненты полного спинового квантового числа.
компоненты полного спинового квантового числа.
 (2.28)
(2.28)
 Компонента спина, перпендикулярная к оси
Компонента спина, перпендикулярная к оси  , равна
, равна  , независимо от номера узла
, независимо от номера узла  и независимо от времени. Для малых амплитуд, когда
и независимо от времени. Для малых амплитуд, когда  , для
, для  компоненты имеем:
компоненты имеем:
 (2.29)
(2.29)
Согласно квантовой теории, для разности  существуют только целочисленные значения. Если
существуют только целочисленные значения. Если 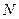 – полное число спинов,
– полное число спинов,  –
–  – компонента полного спина, когда возбуждена спиновая волна
– компонента полного спина, когда возбуждена спиновая волна  : то условие квантования для спиновой волны с амплитудой
: то условие квантования для спиновой волны с амплитудой 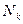 :
:

 (2.30)
(2.30)
 – целое число, равное количеству магнонов, возбужденных с волновым вектором
– целое число, равное количеству магнонов, возбужденных с волновым вектором  . Любой магнон уменьшает
. Любой магнон уменьшает  – компоненту полного спина на 1. Энергия магнонов удовлетворяет квантовому условию и ровна:
– компоненту полного спина на 1. Энергия магнонов удовлетворяет квантовому условию и ровна:

 (2.31)
(2.31)
Тепловое возбуждение магнонов.
 При тепловом равновесии
При тепловом равновесии  определяется функцией распределения Планка:
определяется функцией распределения Планка:
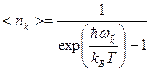 (2.32)
(2.32)
Полное число магнонов возбужденных при температуре 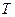 :
:

 (2.33)
(2.33)
 – число магнонных мод на единичный частотный интервал.
– число магнонных мод на единичный частотный интервал.
Интеграл берется по всем разрешенным значениям 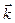 в первой зоне Бриллюена. При достаточно низких температурах пределы интегрирования можно брать от 0 до
в первой зоне Бриллюена. При достаточно низких температурах пределы интегрирования можно брать от 0 до 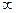 , так как
, так как  экспоненциально, при
экспоненциально, при  .
.
Функция плотности мод для магнонов:

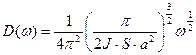 (2.34)
(2.34)

 (2.35)
(2.35)


Число атомов 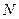 на единицу объема равно
на единицу объема равно  , где
, где  = 1, 2 или 4, соответственно для простой кубической, ОЦК и ГЦК решеток. Так как отношение
= 1, 2 или 4, соответственно для простой кубической, ОЦК и ГЦК решеток. Так как отношение  равно относительному изменению намагниченности:
равно относительному изменению намагниченности:

 (2.36)
(2.36)
 – закон
– закон  Блоха.
Блоха.
 добавка
добавка  – увеличение энергии.
– увеличение энергии.

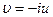 , решение описывает круговую прецессию любого спина относительно оси
, решение описывает круговую прецессию любого спина относительно оси 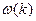 . Для спиновых волн в одномерной системе для модели, в которой учитывается взаимодействие лишь ближайших соседей. В случае длинных волн
. Для спиновых волн в одномерной системе для модели, в которой учитывается взаимодействие лишь ближайших соседей. В случае длинных волн