Главная | Обратная связь

Тема 2. Похибки обчислень

Дії над наближеними числами

Похибки обчислень

Нехай , і задані абсолютні і відносні похибки їх наближень, тобто: , ; , .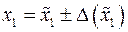

Сформулюємо правила обчислення похибок при виконуванні операцій над наближеними числами.

1. При додаванні або відніманні двох наближених чисел їх абсолютні похибки додаються:

.

2. При множенні або діленні двох наближених чисел їх відносні похибки додаються:

;

.

3. При піднесенні до степеня наближеного числа його відносна похибка множиться на показник степеня:

4. Відносна похибка суми додатних доданків міститься між найбільшим і найменшим значеннями відносних похибок цих доданків:

,

де , .

На практиці для оцінки похибки приймають найбільше значення .

Зауваження.Операції додавання, множення та ін. наближених чисел не є звичайними арифметичними операціями, вони наближено зображають звичайні арифметичні операції. Крім того, наближені арифметичні операції мають зовсім інші властивості, ніж точні. Наприклад, вони не є асоціативними, не виконується закон дистрибутивності, добуток ненульових множників може виявитися рівним нулю („виникнення машинного нуля при множенні”).

Приклад. Обчислити і визначити похибки результату, використовуючи правила обчислення похибок для арифметичних операцій:

,

де , , .

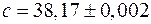Розв’язання. Обчислимо:

.

Визначимо відносні похибки даних:

;

;

.

Тоді за правилами 2, 3 обчислення похибок при виконанні арифметичних операцій будемо мати:

.

Визначимо відносні похибки і . За правилом 1

;

.

Тоді

;

.

Отже,

;

.

Таким чином,

;

.

 

Похибки функцій

 

Поряд з наведеними вище правилами обчислення похибок деяких дій над наближеними числами можна записати аналогічні правила і для обчислення значень функцій, аргументами яких є наближені числа. Найбільш повним є загальне правило, засноване на обчисленні приросту (похибки) функції при заданих приростах (похибках) аргументів.

Розглянемо функцію однієї змінної . Нехай – наближене значення аргументу , – його абсолютна похибка. Абсолютну похибку функції можна вважати її приростом, який вона набуває при зміні аргументу на . З курсу математичного аналізу відомо (J), що цей приріст можна замінити диференціалом:

.

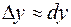Тоді для абсолютної похибки функції отримаємо вираз:

.

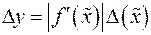Аналогічний вираз можна записати для функції декількох змінних. Так, для абсолютної похибки функції , наближені значення аргументів якої відповідно, абсолютна похибка має вигляд:

, (4)

де , , – абсолютні похибки аргументів.

Формула (4) називається загальною формулою похибок.

Відносна похибка знаходиться за формулою:

. (5)

Отримані співвідношення можна використовувати для виведення похибок довільної функції. Зокрема, таким способом легко отримати вирази правил 1-3 обчислення похибок.

Приклад 6. Обчислити і визначити похибки результату, використовуючи загальну формулу похибок:

,

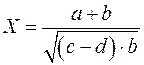де , , .

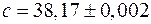Розв’язання. Обчислимо (див. Приклад 5.)

.

За загальною формулою похибок:

.

.