Работа расширения системы и физический смысл

универсальной газовой постоянной

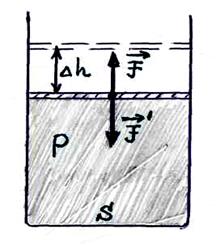
Рассмотрим систему (газ) в цилиндрическом сосуде с гладкими стенками и подвижным невесомым поршнем. Система оказывает на поршень давление Р. Пусть произошло расширение системы, в результате чего поршень поднялся на малую величину .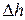

Система (газ под поршнем) при этом совершает работу по преодолению сопротивления внешних тел:

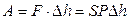или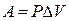

При переходе к бесконечно малым величинам имеем выражение для элементарной работы:

В общем случае при равновесных изменениях объёма от V₁ до V₂: . Если P = const, то A₁₂= P(V₂ – V₁).

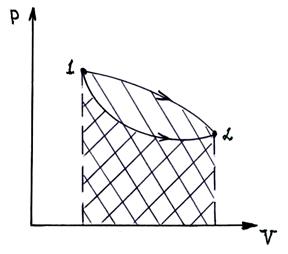Геометрический смысл работы (как и геометрический смысл определенного интеграла) – площадь под кривой, которая графически определяет зависимость P = P(V).

Выражение для элементарной работы , но не dA означает, что элементарная работа не есть полный дифференциал. Работа А₁₂ зависит от того, посредствам какого процесса переходит система из состояния 1 в состояние 2. Таким образом, работа является функцией процесса, но не функцией состояния системы.

При перемещении поршня и внешние тела совершают работу. По III закону Ньютона . Поэтому , то есть работа внешних сил при перемещении поршня равна взятой с противоположным знаком работе сил, действующих со стороны газа на поршень при его перемещении. Это утверждение носит достаточно общий смысл, охватывающий вопрос работы газа и работы внешних сил при расширении газа, находящегося не только под поршнем.

Для установления физического смысла универсальной газовой постоянной запишем уравнение Клапейрона-Менделеева для 1 моля газа: . Продифференцируем данное уравнение при условии, что давление является постоянным: . Однако . Следовательно:

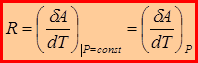– универсальная газовая постоянная численно равна работе изобарического расширения одного моля газа при его нагревании на один кельвин.

Для нормальных условиях:

, где P_О= 101325 Па, Т_О=273,15 К, V_O = 0,022414 м³/моль. Отсюда:

⇐ Предыдущая 123 Следующая ⇒