Главная | Обратная связь

Определение ошибок косвенного измерения физической

Величины

 

Пусть некоторая физическая величина a определяется не прямо, а вычисляется по формуле вида

где х - величина, которую непосредственно измеряют.

Если при измерении величины х допускается абсолютная ошибка х, то она, соответственно, вызывает появление ошибки 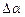при определении 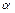. Очевидно, что

Разлагаем правую часть выражения в ряд Тейлора

При достаточно точных измерениях абсолютная ошибка х является весьма малой величиной.

Квадрат и более высокие степени х будут являться малы­ми величинами более высокого порядка, лежащими за пределами точности измерений. Поэтому членами ряда, содержащими х в степенях выше первой, будем пренебрегать. Таким образом, по­лучим:

Так как , то .

В силу малости величин и 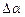будем рассматривать их как дифференциалы . Если теперь определить относительную ошибку

то нетрудно видеть, что это дифференциал натурального логарифма функции f(x): E = d(lnf(x)). Во многих случаях искомая величина a определяется совокупностью нескольких измеряемых величин

Аналогичным методом можно показать, что ошибки при измерении величин вызывают соответствующие ошибки величины a, которые будут определяться частными производными этой функции по определённому аргументу

...........................................

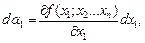
Полная абсолютная ошибка для наиболее неблагоприятного случая равна сумме абсолютных значений всех членов. Если определить теперь относительную ошибку, то полу­чим, что она равна полному дифференциалу натурального лога­рифма этой функции. Во многих случаях оказывается проще сна­чала определить относительную ошибку, а затем абсолютную

Рассмотрим это на примере удельного сопротивления (ρ), исходная формула: , где - измеряемое сопротивление образца; l – длина образца, или расстояние между зондами при компенсационном методе измерения; S – площадь поперечного сечения , где d – толщина образца, h – ширина образца.

Удельное сопротивление

При компенсационном методе измерений (рис. 9)

где - величина эталонного сопротивления; - падение напряжения на эталонном сопротивлении; - падение напряжения между контактами.

Окончательно:

 

 

Натуральный логарифм выражения, полученного для ρ:

 

Дифференцируем, заменяем дифференциалы ошибками отдельных измерений, берём абсолютные значения слагаемых и получаем относительную ошибку:

Примечание: при компенсационном методе измерения определяется падение напряжения между зондами и падение напряжения на эталонном сопротивлении , включённом последовательно с образцом. Так как через сопротивления и протекает тот же самый ток, то и, следовательно:

.

Величины, стоящие в числителе дробей правой части, представляют собой абсолютные ошибки отдельных измерений.

Определив относительную ошибку, подсчитаем абсолютную

и запишем окончательный результат так:

При косвенном измерении физической величины рекомендован следующий порядок вычисления ошибок:

1) определяются значения непосредственно измеряемых величин и абсолютные ошибки этих измерений ;

2) подставляют значения измеряемых величин в выражение и определяют значение ;

3) логарифмируем выражение , беря натуральный логарифм;

4) дифференцируем полученное логарифмическое выражение;

5) дифференциалы 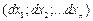заменяются абсолютными ошибками измерений . В полученном дифференциальном выражении берутся абсолютные значения отдельных членов. Подставляются значения непосредственно измеряемых величин и подсчитывается относительная ошибка, которая выражается в виде десятичной дроби;

6) определяется абсолютная ошибка 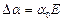и записывается окончательный результат: .

На практике встречаются случаи, когда при вычислении относительной ошибки необходимо вносить некоторые поправки в расчетную формулу. Таким примером может служить формула вида

,

когда измеряемая величина входит и в числитель и в знаменатель выражения. Такой вид имеет формула сопротивления цепи, со­стоящей из двух параллельно включенных сопротивлений, фор­мула для вычисления фокусного расстояния линзы и т. д.

Выражение, полученное по общему методу для вычисления относительной ошибки, имеет вид:

.

Анализ показывает, что в этом случае можно получить за­метное преувеличение величины вычисляемой ошибки, Возьмем конкретный пример: b = 20, c = 30,

.

По вышеприведенной формуле получим

.

Можно прикинуть значение максимальной ошибки, под­ставив в выражение для a значения измеряемых величин с по­правками

.

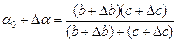Подставив значения, взяв поправки со знаком "+", получим:

, .

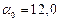Таким образом, , а

.

Измеряемые величины входят и в числитель и в знаменатель ис­ходного выражения a.

Ели ошибка имеет положительный знак, то прибавлен­ная к значению b в числителе, она увеличивает среднее значение , а прибавленная к значению b в знаменателе, она уменьшает среднее значение . Таким образом, точность среднего результа­та может уменьшиться.

Учитывая этот факт, относительную ошибку можно оп­ределить по формуле:

.

Подстановка значений приводит к результату

 

.