 |
|
Просторова система сил.
Рівненський педагогічний інститут
Кафедра загальнотехнічних дисциплін
А. О. Сяський
Технічна механіка
(Статика)
Текст лекцій
Рівне-1993
Передмова
Предмет „Технічна механіка” — комплекс найважливіших загально технічних знань, який складається із трьох частин: статика, кінематика і динаміка.
Об’єднання трьох основних дисциплін — “Теоретична механіка”, „Опір матеріалів”, „Теорія механізмів і машин” — в інтегрований курс “Технічна механіка” дає можливість формувати у студентів єдиний погляд на технічні науки і цілісний світогляд. При цьому, на основі глибоких і органічних зв’язків з фізикою, математикою і практикумом в навчальних майстернях, забезпечується плавний перехід від природничих (теоретична механіка) до технічних (опір матеріалів, ТММ) дисциплін, виключається дублювання окремих тем, а також досягається єдність умовних позначень символів і термінології.
Структура курсу дозволяє теоретичні положення конкретизувати в практичних задачах опору матеріалів та теорії механізмів і машин, забезпечуючи при цьому логічний перехід від простого до складного.
У першій частині посібника („Статика”) вивчається статика абсолютно твердого тіла і статика деформованого твердого тіла (опір матеріалів), що забезпечує викладення програмного матеріалу з єдиних позицій.
При вивченні другої („Кінематика”) і третьої („Динаміка”) частин об’єкти руху розглядаються в такій послідовності: матеріальна точка (основний об’єкт), тверде тіло, система матеріальних точок, механізм (система твердих тіл), машина (система механізмів).
Такий підхід до вивчення програмового матеріалу дозволяє на кожному наступному етапі навчання використовувати конкретні знання, здобуті студентами на попередніх.
Навчальний посібник написаний у відповідності з програмою курсу „Технічна механіка”, затвердженою Радою Інституту (протокол №8 від 23 02 1989 р.).
Автор висловлює свою щиру вдячність доценту кафедри опору матеріалів і будівельної механіки УІІВГ Мартиненку А.О. за надану допомогу у редагуванні рукопису.
ЧАСТИНА ПЕРША
СТАТИКА
ГЛАВА І. СТАТИКА ТВЕРДОГО ТІЛА
§І. Основні поняття і завдання статики
Статикою називається розділ механіки, в якому розглядається рівновага матеріальних тіл під дією заданих сил і задача зведення системи сил до найпростішого виду.
Основні поняття статики ввійшли в науку як результат багатовікової практичної діяльності людини. Вони підтверджені дослідами і спостереженнями над явищами природи. Щоб глибше вивчити ті чи інші сторони деякого явища, в науці широко використовують метод абстракцій, зосереджуючи увагу на найбільш суттєвих сторонах явища, відкидаючи другорядні деталі. В курсі статики подібного роду абстракціями є поняття матеріальної точки, абсолютно твердого тіла і сили.
Матеріальною точкою (МТ) будемо називати реальне фізичне тіло, розмірами якого в умовах розглядуваної задачі можна знехтувати. МТ відрізняється від геометричної точки тим, що в першій зосереджена певна кількість речовини. Будь-яке тверде тіло в механіці можна подати як систему МТ. Під останньою розуміємо сукупність матеріальних частинок, які певним чином взаємодіють між собою.
Абсолютно твердим тілом (АТТ) називається фізичне тіло, в якому відстані між довільними його точками за всіх умов залишаються незмінними. Іншими словами, АТТ зберігає незмінну геометричну як в цілому, так і кожної своєї частини зокрема, тобто не деформується. АТТ можуть вступати у взаємодію, в результаті якої змінюється не тільки їх положення в просторі, але й швидкості їх точок.
Силами в механіці називають кількісну міру взаємодії матеріальних тіл. Маючи на увазі задачі статики, ми будемо розуміти під силою дію одного тіла на інше, яка проявляється у вигляді тиску, протягування або відштовхування. Сила — величина векторна. Її дія на тіло визначається: 1) числовим значенням або модулем сили; 2) напрямом дії сили; 3) точкою прикладання сили. Виходячи з цього, можна зробити висновок, що сила в механіці — закріплений вектор.
Величина сили визначається шляхом порівняння її з силою, прийнятою за одиницю виміру. В Міжнародній системі одиниць СІ одиницею сили є ньютон (Н).
Напрямок і точка прикладання сили залежать від характеру взаємодії тіл і їх взаємного розміщення. Наприклад, сила тяжіння, що діє на деяке тіло, направлена вертикально вниз (до центра Землі).
Як і кожний вектор, графічно сила зображується направленим відрізком із стрілкою. Довжина цього відрізка (АВ на мал.1.1) у вибраному масштабі виражає числове значення, яке будемо позначати символами F або  .Точка А — точка прикладання сили. Пряма АВ, вздовж якої направлена сила
.Точка А — точка прикладання сили. Пряма АВ, вздовж якої направлена сила  ,називається лінією дії сили.
,називається лінією дії сили.
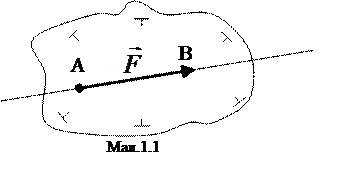 За характером дії сили поділяються на зовнішні, які діють на тіло з боку інших матеріальних тіл, і внутрішні (сили взаємодії між частинами тіла). Якщо сила прикладена до тіла в одній його точці, то вона називається зосередженою. Всі інші сили називаються розподіленими. Поняття зосередженої сили умовне, бо практично прикласти силу до тіла в одній його точці неможливо.
За характером дії сили поділяються на зовнішні, які діють на тіло з боку інших матеріальних тіл, і внутрішні (сили взаємодії між частинами тіла). Якщо сила прикладена до тіла в одній його точці, то вона називається зосередженою. Всі інші сили називаються розподіленими. Поняття зосередженої сили умовне, бо практично прикласти силу до тіла в одній його точці неможливо.
Розглянемо ряд означень, необхідних для логічного викладу матеріалу:
1. Якщо тверде тіло не зв’язане з іншими тілами і йому можна надати довільне переміщення в просторі, то воно називається вільним. При наявності певних обмежень в його рух, тіло називається невільним. Матеріальні тіла, які обмежують рух даного, називаються в’язями.
2. Сукупність сил, що діють на задане АТТ, будемо називати системою сил.
3. Якщо одну систему сил, що діє на вільне АТТ, можна замінити іншою системою, не змінюючи стану тіла, то такі системи сил називають еквівалентними.
4. Якщо під дією системи сил тіло перебуває в стані спокою або рівномірного прямолінійного руху, то такий стан тіла називається рівновагою.
5. Система сил, під дією якої тіло перебуває у рівновазі, називається зрівноваженою, або еквівалентною нулю.
6. Якщо система сил еквівалентна одній силі, то ця сила називається рівнодійною даної системи сил.
Для того, щоб під дією системи сил вільне тіло перебувало у рівновазі (статика вивчає рівновагу твердих тіл під дією прикладених до них сил), необхідно, щоб ці сили задовольняли певним умовам рівноваги. Знаходження цих умов є одна із основних задач статики. Але для їх відшукання, а також для розв’язування інших задач механіки, необхідно уміти додавати сили, замінювати дію на тіло однієї системи сил іншою. Тому в статиці твердого тіла розглядаються такі дві основні задачі:
1. Зведення системи сил, що діє на тверде тіло, до найпростішого виду (перша задача статики).
2. Визначення умов рівноваги системи сил, що діють на тверде тіло (друга задача статики).
Задачі статики можуть бути розв’язані шляхом відповідних геометричних побудов (геометричний метод) або за допомогою числових розрахунків (аналітичний метод).
§2. Аксіоми статики
Застосування методу абстракції і узагальнення результатів багатовікового досвіду, безпосередніх спостережень і виробничої діяльності людини дозволили встановити ряд вихідних положень, що приймаються без математичного доведення і називаються аксіомами. В них зафіксовані основні властивості сил, якими дозволено користуватися при побудові курсу статики.
Аксіома 1. Під дією двох сил вільне АТТ перебуває у рівновазі тоді і тільки тоді, коли ці сили однакові за величиною, протилежні за напрямком і діють вздовж однієї прямої (мал. 1.2).

Аксіома 1 визначає найпростішу зрівноважену систему сил, так як досвід показує, що вільне тіло під дією цієї сили не перебуває у рівновазі.
Аксіома 2. Дія заданої системи сил на АТТ не зміниться, якщо до неї прикласти або відкинути зрівноважену систему сил.
Ця аксіома показує, що дві системи сил, які відрізняються на зрівноважену систему, еквівалентні.
Наслідок. Сила в статиці — ковзний вектор. Це означає, що силу можна довільно переміщати вздовж її лінії дії. Нехай на АТТ діє прикладена в точці А сила  (мал. 1.3). Виберемо на лінії дії сили довільну точку В і прикладемо дві зрівноважені сили
(мал. 1.3). Виберемо на лінії дії сили довільну точку В і прикладемо дві зрівноважені сили  і
і  (аксіома 2) такі, що
(аксіома 2) такі, що  =
=  ,
,  = -
= -  . Сили
. Сили  і
і  по аксіомі 1 утворюють зрівноважену систему сил, яку можна від кинути. Отже, на тіло буде діяти лише сила
по аксіомі 1 утворюють зрівноважену систему сил, яку можна від кинути. Отже, на тіло буде діяти лише сила  , яка дорівнює силі
, яка дорівнює силі  , але прикладена в точці В. здобутий результат справедливий лише для АТТ.
, але прикладена в точці В. здобутий результат справедливий лише для АТТ.
Аксіома 3. (Аксіома паралелограма сил). Рівнодійна двох сил, прикладених в одній точці АТТ, визначається діагоналлю паралелограма, побудованого на силах, як на сторонах, і прикладеного в цій точці (мал.1.4).
Вектор  , побудований на векторах
, побудований на векторах  і
і  , називається їх сумою
, називається їх сумою
 (1.1)
(1.1)
Його модуль визначається за формулою
 (1.2)
(1.2)
 Аксіома 3 визначає правило додавання двох сил, прикладених в одній точці. Вона дозволяє довести теорему про три сили: якщо під дією трьох непаралельних сил, що діють в одній площині, АТТ перебуває у рівновазі, то лінії дії сил перетинаються в одній точці.
Аксіома 3 визначає правило додавання двох сил, прикладених в одній точці. Вона дозволяє довести теорему про три сили: якщо під дією трьох непаралельних сил, що діють в одній площині, АТТ перебуває у рівновазі, то лінії дії сил перетинаються в одній точці.
Доведення. Нехай тіло перебуває у рівновазі під дією сил  ,
,  ,
,  , розміщених в одній площині і прикладених відповідно в точках А1, А2, А3 (мал. 1.5).
, розміщених в одній площині і прикладених відповідно в точках А1, А2, А3 (мал. 1.5).
Перенесемо сили  і
і  в точку О і замінимо їх силою
в точку О і замінимо їх силою  по правилу паралелограма. Замість системи сил
по правилу паралелограма. Замість системи сил  ,
,  ,
,  дістали еквівалентну їй систему
дістали еквівалентну їй систему  ,
,  . Оскільки задана система сил зрівноважена, то за аксіомою і лінія дії сили
. Оскільки задана система сил зрівноважена, то за аксіомою і лінія дії сили  проходить через точку О. Теорема доведена.
проходить через точку О. Теорема доведена.
Зауважимо, що обернена теорема не має місце місця.
 Аксіома 4. Сили взаємодії між двома твердими тілами завжди однакові за величиною, протилежні за напрямком і діють по прямій (мал. 1.6). Аксіома 6 є не що інше, як відомий третій закон Ньютона. Слід визначити, що сили
Аксіома 4. Сили взаємодії між двома твердими тілами завжди однакові за величиною, протилежні за напрямком і діють по прямій (мал. 1.6). Аксіома 6 є не що інше, як відомий третій закон Ньютона. Слід визначити, що сили  і
і  не утворюють зрівноважену систему сил, бо вони прикладені до різних тіл. На основі даної аксіоми легко довести, що внутрішні сили, які діють в АТТ, утворюють зрівноважену систему сил і на умови рівноваги не впливають.
не утворюють зрівноважену систему сил, бо вони прикладені до різних тіл. На основі даної аксіоми легко довести, що внутрішні сили, які діють в АТТ, утворюють зрівноважену систему сил і на умови рівноваги не впливають.
Аксіома 5. Якщо деяка система сил зрівноважена на одному АТТ, то вона буде зрівноважена і на будь-якому іншому тілі. В силу цієї аксіоми форма і розміри тіл несуттєві при визначенні статики. Це діє змогу замінити термін «рівновага АТТ під дією системи сил» на термін «рівновага системи сил».
Аксіома 6. (Принцип затвердіння).Якщо деформоване тіло під дією системи сил перебуває у рівновазі, то при його затвердінні рівновага не порушиться. Дана аксіома показує, що при рівновазі твердого і деформованого тіл повинні виконуватися одні і ті ж умови, однак для деформованого тіла ці умови, будучи необхідними, можуть бути достатніми. Розглянемо невільне АТТ, рух якого обмежений певними в’язами. Сили взаємодії заданого тіла і в’язі називаються силами реакції в’язі або реакцією в’язі. Напрямок реакції в’язі завжди направлений в сторону, протилежну до неможливого руху тіла. Ця обставина полегшує визначення напрямків реакції при розв’язуванні задач.
Аксіома 7. (аксіома в’язей). Будь-яке невільне АТТ можна розглядати як вільне, якщо умовно відкинути в’язі, а їх дію замінити відповідними реакціями.
Оскільки в статиці розглядаються умови рівноваги вільного тіла, то, щоб застосувати їх до невільного тіла, потрібно поступити згідно з аксіомою 7.
§3. В’язі та їх реакції
Конструктивно в’язі можуть бути реалізовані у вигляді різного роду опор, шарнірних з’єднань, тяг. Вважаємо, що вони виготовлені із абсолютно твердих матеріалів і тертя в зонах їх контакту з розглядуваними тілами відсутнє.
Розглянемо найбільш характерні типи в’язей і їх реакцій.
1.Гладкий контакт двох поверхонь. Гладкою будемо називати поверхню, тертям об яку даного тіла можна знехтувати. Така поверхня не дозволяє тілу рухатись по спільному перпендикуляру в точці дотику. Тому реакція направлена так, як показано на мал. 1.7. До цього типу в’язей можна віднести так званий рухомий каток (мал.1.7).

Його реакція направлена перпендикулярно до опорної поверхні.
 2.Контакт гладкої поверхні і двогранного кута. Для такої в’язі реакція направлена по перпендикуляру до гладкої поверхні (мал. 1.9).
2.Контакт гладкої поверхні і двогранного кута. Для такої в’язі реакція направлена по перпендикуляру до гладкої поверхні (мал. 1.9).
3.Циліндричний шарнір (підшипник). Розглянемо з’єднання циліндричного болта і тіла, що має циліндричний отвір, діаметр якого дещо більший діаметра болта (мал. 1.10). таке з’єднання називається циліндричним шарніром або підшипником. Оскільки тіло АВ може лише обертатися навколо тіла болта, то реакція  такого шарніра діє в площині, перпендикулярній осі обертання, і проходить через центр О. Циліндричним можна вважати і нерухому опору (мал. 1.11).
такого шарніра діє в площині, перпендикулярній осі обертання, і проходить через центр О. Циліндричним можна вважати і нерухому опору (мал. 1.11).
4.Сферичний шарнір. Цей вид в’язі закріплює певну точку тіла так, що вона не може здійснювати жодних лінійних переміщень в просторі. Реакція сферичного шарніра проходить через його центр і мож мати довільний напрямок у просторі (мал. 1.12).
5.Двошарнірне стержневе з’днання. Нехай в деякій конструкції в’ззю є стержень АВ, закріплений на кінцях шарнірами А, В (мал. 1.13). якщо на стержень не діють зовнішні сили, то реакція направлена вздовж його осі. Цей висновок зроблено на основі аксіоми 1.
6.Гнучка в’язь (нитка, канат, ланцюг). Реакція  називається натягом. Вона прикладена в точці прикріплення до тіла і направлена вздовж нитки всередину її. На мал. 1.14
називається натягом. Вона прикладена в точці прикріплення до тіла і направлена вздовж нитки всередину її. На мал. 1.14  ,
,  — натяги ниток.
— натяги ниток.
7.Жорстке защімлення. Балка АВ одним кінцем замурована в стіні, а інший кінець вільний (мал. 1.15). В даному прикладі реакція защемлення

складається із сили  і пари сил з моментом mA. Визначення реакцій в’язей має важливе практичне значення, бо знаючи їх, ми, згідно аксіоми 4, будемо знати і силу тиску на в’язі, тобто ті вихідні дані, які необхідні для розрахунку міцності відповідних частин конструкції.
і пари сил з моментом mA. Визначення реакцій в’язей має важливе практичне значення, бо знаючи їх, ми, згідно аксіоми 4, будемо знати і силу тиску на в’язі, тобто ті вихідні дані, які необхідні для розрахунку міцності відповідних частин конструкції.
§4. Система збіжних сил
4.1. Додавання збіжних сил. Система сил називається збіжною, якщо лінії їх дії перетинаються в одній точці, яка називається центром. Оскільки силу можна переносити вздовж лінії її дії, то система збіжних сил еквівалентна системі сил, прикладених в центрі.
Розглянемо першу і другу задачі статики для системи збіжних сил.
Заміну даних системи сил, прикладених в одній точці, рівнодійною можна провести шляхом послідовного застосування аксіоми паралелограма. Операцію додавання сил можна виконати, не будуючи кожен раз паралелограм сил, достатньо в кінці В вектора  прикласти початок вектора
прикласти початок вектора  , потім до кінця С вектора
, потім до кінця С вектора  — початок вектора
— початок вектора  і т.д. Сполучивши центр А з кінцем останньої сили, одержимо рівнодійну
і т.д. Сполучивши центр А з кінцем останньої сили, одержимо рівнодійну  (мал. 1.16). Описаний вище спосіб знаходження рівнодійної збіжної системи сил називається правилом многокутника, ламана ABCDE — силовим многокутником, а відрізок АЕ — замикальною стороною многокутника.
(мал. 1.16). Описаний вище спосіб знаходження рівнодійної збіжної системи сил називається правилом многокутника, ламана ABCDE — силовим многокутником, а відрізок АЕ — замикальною стороною многокутника.
 Якщо в точці О задано n збіжних сил
Якщо в точці О задано n збіжних сил  ,
,  ,….
,….  , то їх рівнодійна
, то їх рівнодійна  прикладена в цій же точці і дорівнює геометричній сумі векторів заданих сил
прикладена в цій же точці і дорівнює геометричній сумі векторів заданих сил
 (1.3)
(1.3)
Таким чином, розв’язок першої задачі статики може бути сформульований так: довільна збіжна система сил може бути зведена до рівнодійної, яка визначається з рівності (1.3).
4.2 Розкладання сил. Розкласти дану силу на складові — означає знайти таку систему сил, для яких задана сила буде рівнодійною. Ця задача невизначена і має єдиний розв’язок лише при заданні додаткових умов. Розглянемо два найбільш важливі окремі випадки.
1. Розкладання сили по двох заданих не колінеарних напрямках.
 Розкладемо задану силу
Розкладемо задану силу  (мал. 1.17) по напрямках паралельних прямих АВ і АD. Задача зводиться до побудови паралелограма з діагоналлю
(мал. 1.17) по напрямках паралельних прямих АВ і АD. Задача зводиться до побудови паралелограма з діагоналлю  і сторонами, паралельними прямим АВ і АD. Для розв’язку задачі проводимо через точки А, С прямі, паралельні АВ і АD. Сили
і сторонами, паралельними прямим АВ і АD. Для розв’язку задачі проводимо через точки А, С прямі, паралельні АВ і АD. Сили  і
і  будуть шуканими складовими.
будуть шуканими складовими.
 2. Розкладання сили по трьох не компліментарних напрямках. Якщо задані напрямки не лежать в одній площині, то задача визначена і зводиться до побудови такого паралелепіпеда, у якого діагональ зображує силу
2. Розкладання сили по трьох не компліментарних напрямках. Якщо задані напрямки не лежать в одній площині, то задача визначена і зводиться до побудови такого паралелепіпеда, у якого діагональ зображує силу  , а ребра паралельні заданим напрямкам (мал. 1.18). зауважимо, що розв’язки приведених вище двох задач відповідають теоремам шкільного курсу геометрії про розклад вектора на площині по двох не колінеарних і в просторі по трьох не компліментарних векторах.
, а ребра паралельні заданим напрямкам (мал. 1.18). зауважимо, що розв’язки приведених вище двох задач відповідають теоремам шкільного курсу геометрії про розклад вектора на площині по двох не колінеарних і в просторі по трьох не компліментарних векторах.
4.3 Проекція сили на вісь і площину. Розглянемо вісь l і силу  , що визначається точками А,В (мал. 1.19). введемо такі означення:
, що визначається точками А,В (мал. 1.19). введемо такі означення:
 1. Геометричною проекцією сили
1. Геометричною проекцією сили  на вісь l будемо називати вектор
на вісь l будемо називати вектор  , точки якого визначаються як ортогональні проекції точок А, В на вісь l
, точки якого визначаються як ортогональні проекції точок А, В на вісь l
 (1.4)
(1.4)
2. Алгебраїчною проекцією сили  на вісь l називається число зі знаком, яке визначається рівністю
на вісь l називається число зі знаком, яке визначається рівністю
 (1.5)
(1.5)
Знак «+» вибираємо тоді, коли вектор  спів напрямлений з віссю l (
спів напрямлений з віссю l (  ). По величині проекція сили на вісь дорівнює добутку величини сили
). По величині проекція сили на вісь дорівнює добутку величини сили  на косинус кута між силою і додатнім напрямком осі l
на косинус кута між силою і додатнім напрямком осі l
 (1.6)
(1.6)
При цьому проекція сили буде додатною, якщо відповідний кут гострий, і від’ємною, якщо цей кут — тупий.
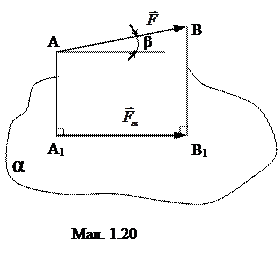 Зауважимо, що при подальшому викладі матеріалу під терміном «проекція сили на вісь» будемо розуміти алгебраїчну проекцію.
Зауважимо, що при подальшому викладі матеріалу під терміном «проекція сили на вісь» будемо розуміти алгебраїчну проекцію.
3. Проекція сили на площину. Розглянемо силу  і площину α (мал. 1.20). спроектуємо точки А, В, що визначають силу
і площину α (мал. 1.20). спроектуємо точки А, В, що визначають силу  , ортогонально на площину α
, ортогонально на площину α

Величина проекції обчислюється за формулою  , де β — кут між силою
, де β — кут між силою  і площиною α.
і площиною α.
В деяких випадках для знаходження проекції сили на вісь буває зручніше знайти спочатку її проекцію на площину, в якій дана вісь розміщена, а потім знайдений вектор спроектувати на задану вісь. Такий метод носить назву подвійного проектування сили на вісь.
Для ефективного розв’язку другої задачі статики розглянемо без доведення основні властивості проекцій вектора на вісь: а) рівні вектори мають рівні проекції; б) проекція геометричної сум векторів на деяку вісь дорівнює алгебраїчній сумі проекцій складових на цю вісь.
Доведення цих тверджень проводиться у курсі вищої математики (розділ «Векторна алгебра»).
4.4. Умови рівноваги системи збіжних сил. Оскільки система збіжних сил зводиться до однієї сили /рівнодійної/, то її рівновага можлива лише у випадку  . Так як рівнодійна
. Так як рівнодійна  визначається як замикальна сторона силового многокутника, то у випадку рівноваги він повинен бути замкненим.
визначається як замикальна сторона силового многокутника, то у випадку рівноваги він повинен бути замкненим.
Отже, для рівноваги системи збіжних сил необхідно і достатньо, щоб силовий многокутник, побудований з цих сил, був замкнений. Останнє твердження виражає собою геометричну умову рівноваги.
Для встановлення алгебраїчних умов рівноваги виберемо просторову систему координат Оxyz, відносно якої задані сили характеризуються такими проекціями
 причому
причому
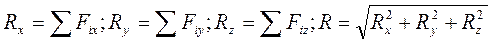 (1.7)
(1.7)
Прирівнюючи до нуля проекції рівнодійної, дістанемо
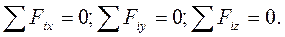 (1.8)
(1.8)
Рівності (1.8) виражають умови рівноваги в алгебраїчній формі: для рівноваги просторової системи збіжних сил необхідно і достатньо, щоб суми проекцій цих сил на кожну із координатних осей дорівнювали нулю.
У випадку абсолютної рівноваги тіла (спокою) умови (1.8) забезпечують відсутність переміщення тіла в напрямках координатних осей. Якщо всі сили діють в одній площині (плоска система сил), то умови рівноваги (1.8) приймають вид
 (1.9)
(1.9)
Геометрична умова рівноваги або рівності (1.8) являють собою розв’язок другої задачі статики для системи збіжних сил.
Схема розв’язування задач статики
1. Вибираємо тіло (основний об’єкт), рівновага якого буде розглядатися. Якщо задані сили діють на одне тіло, а шукані на інше, то може виникнути необхідність розглянути послідовно рівновагу кожного тіла окремо
2. Звільняємо тіло від в’язей, замінюючи їх дію невідомими реакціями. Зображуємо всі діючі на тіло задані сили і сили реакцій. При цьому тіло, звільнене від в’язей, слід зобразити окремо.
3. Складаємо умови рівноваги. Вид цих умов залежить від виду системи сил, що діє на розглядуване тіло після його звільнення від в’язей, і який метод (графічний чи аналітичний) застосовується.
4. Визначаємо шукані величини, перевіряємо правильність розв’язку і досліджуємо здобуті результати.
 Приклад 1. Балка АВ одним кінцем А закріплена на нерухомій опорі циліндричним шарніром, а другим кінцем В покладена на рухомий каток (мал. 1.21). в точці D прикладена сила
Приклад 1. Балка АВ одним кінцем А закріплена на нерухомій опорі циліндричним шарніром, а другим кінцем В покладена на рухомий каток (мал. 1.21). в точці D прикладена сила  . Визначити реакції опор в точках А і В.
. Визначити реакції опор в точках А і В.
Розв’язування. Основним тілом, рівновага якого буде розглядатися, є балка АВ. Звільняємо її від в’язей А, В. реакція в опорі В направлена вертикально, а в опорі А — напрямок реакції невідомий. Для його знаходження використаємо теорему про три сили. Реакція  направлена вздовж прямої AS. Для визначення кута α розглянемо прямокутний трикутник DBS
направлена вздовж прямої AS. Для визначення кута α розглянемо прямокутний трикутник DBS
DS=DB/cos60º=2DB.
Отже, ∆ASD — рівнобедрений (AD=DS).
 Геометричний метод. Умови рівноваги сил
Геометричний метод. Умови рівноваги сил  ,
, 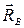 ,
, 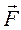 запишемо у вигляді
запишемо у вигляді  +
+ 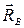 +
+ 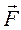 =0.
=0.
Побудуємо замкнений трикутник (мал. 1.22) сил, вибираючи для них певний масштаб. З цього трикутника знаходимо  =
= 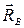 =
= 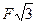 .
.
Аналітичний метод. Складаємо умови рівноваги плоскої системи збіжних сил.


Покладаємо α=30º.
Відповідь:  =
= 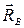 =
= 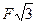 .
.
§5. Система двох паралельних сил. Теорія пар на площині.
Система сил називається плоскою, якщо лінії дії сил лежать в одній площині. Система двох паралельних сил, що діють по різних прямих, завжди плоска.
5.1. Додавання двох паралельних сил. На відміну від двох збіжних сил, для додавання паралельних сил  і
і  , прикладених в точках А, В твердого тіла, не можна безпосередньо використати правило паралелограма. Тут можливі два випадки: 1) сили направлені в один бік; 2) сили направлені в протилежні боки.
, прикладених в точках А, В твердого тіла, не можна безпосередньо використати правило паралелограма. Тут можливі два випадки: 1) сили направлені в один бік; 2) сили направлені в протилежні боки.
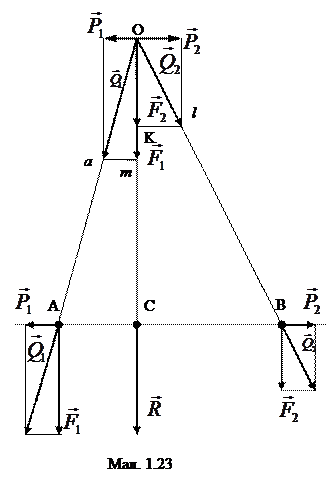 1) Додавання двох сил, направлених в один бік. Розглянемо тверде тіло (мал. 1.23), на яке діють дві паралельні сили
1) Додавання двох сил, направлених в один бік. Розглянемо тверде тіло (мал. 1.23), на яке діють дві паралельні сили  і
і  . Прикладемо в точках А і В зрівноважену систему сил
. Прикладемо в точках А і В зрівноважену систему сил  і
і  , які направлені вздовж АВ(
, які направлені вздовж АВ(  =-
=-  ), і додамо їх до сил
), і додамо їх до сил  ,
,  за правилом паралелограма. Знайдені сили
за правилом паралелограма. Знайдені сили  і
і  перенесемо в точку О, в якій перетинаються лінії їх дії, і розкладемо на початкові складові. Після цього в точці О будуть діяти дві зрівноважені сили
перенесемо в точку О, в якій перетинаються лінії їх дії, і розкладемо на початкові складові. Після цього в точці О будуть діяти дві зрівноважені сили 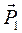 і
і  , які відкидаємо, і дві паралельні сили
, які відкидаємо, і дві паралельні сили  ,
,  , що діють по одній прямій. Ці сили перенесемо в точку С і замінимо рівнодійною
, що діють по одній прямій. Ці сили перенесемо в точку С і замінимо рівнодійною  , величина якої дорівнює
, величина якої дорівнює
К = F1 + F2 (1/10)
Сила  буде рівнодійною сил
буде рівнодійною сил  і
і  , прикладених в точках А і В. Для визначення положення точки С розглянемо трикутники ОАС, Оak, OCb, Omb. З умов подібності відповідних трикутників маємо
, прикладених в точках А і В. Для визначення положення точки С розглянемо трикутники ОАС, Оak, OCb, Omb. З умов подібності відповідних трикутників маємо
AC / OC = P1 / F1 ; BC / OC = P2 / F2,
або AC * F1 = BC * F2 , бо P1 = P2
Враховуючи властивості пропорцій і рівності АВ = АС + СВ, R = F1 + F2, знаходимо BC/F1 = AC/F2 = AB/R. (1.11)
Співвідношення (1.11) мають назву правила важеля першого роду. Вони дозволяють розв’язувати обернену задачу про розклад сили  на дві паралельні складові
на дві паралельні складові  і
і  .
.
Отже, рівнодійна двох співнаправлених паралельних сил має той самий напрям, що і складові, її величина визначається за формулою (1.10), а точка прикладення С — із співвідношення (1.11).
2) Додавання двох сил, направлених в протилежні боки. Розглянемо дві антипаралельні сили  і
і  , які прикладені в точках А і В твердого тіла, причому будемо вважати, що
, які прикладені в точках А і В твердого тіла, причому будемо вважати, що  >
>  . На прямій АВ з боку більшої сили виберемо точку С і прикладемо в ній зрівноважені сили
. На прямій АВ з боку більшої сили виберемо точку С і прикладемо в ній зрівноважені сили  і
і  , паралельні силам
, паралельні силам  і
і  (мал. 1.24). при цьому величина цих сил і положення точки С визначаються рівностями R = F1 – F2; (1.12)
(мал. 1.24). при цьому величина цих сил і положення точки С визначаються рівностями R = F1 – F2; (1.12)
BC/F2 = AC/F1 = AB/R  (1/13)
(1/13)
Додавши сили  і
і  , за формулами (1.10) і (1.11) визначимо силу
, за формулами (1.10) і (1.11) визначимо силу 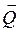 , яка разом з силою
, яка разом з силою  утворює зрівноважену систему сил. В результаті цього задані сили будуть замінені рівнодійною
утворює зрівноважену систему сил. В результаті цього задані сили будуть замінені рівнодійною  , величина якої і положення визначаються рівностями (1.12), (1.13), причому остання називається правилом важеля другого роду.
, величина якої і положення визначаються рівностями (1.12), (1.13), причому остання називається правилом важеля другого роду.
Таким чином, система двох паралельних сил, направлених в протилежні боки, зводиться до рівнодійної, яка має напрямок більшої сили, її величина визначається формулою (1.12), а точка прикладання — із співвідношень (113).
3) Пара сил. Розглянемо випадок антипаралельних сил при F1 = F2 (мал. 1.25). Така система сил називається парою сил або парою. Оскільки сили  і
і  діють по різних прямих, то згідно аксіоми 1 пара сил не перебуває у рівновазі. В той же час пара сил не має рівнодійної. Якщо допустити протилежне, що пара (
діють по різних прямих, то згідно аксіоми 1 пара сил не перебуває у рівновазі. В той же час пара сил не має рівнодійної. Якщо допустити протилежне, що пара (  і
і  ) має рівнодійну
) має рівнодійну  , то сила
, то сила  повинна цю пару зрівноважити. На основі теореми про три сили
повинна цю пару зрівноважити. На основі теореми про три сили  ,
,  ,
, 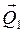 повинні перетинатися в одній точці, що неможливо. Таким чином, пару сил не можна замінити або зрівноважити однією силою. Пара сил — самостійний об’єкт в статиці твердого тіла. Під час дії на тіло вона приводить до його обертання.
повинні перетинатися в одній точці, що неможливо. Таким чином, пару сил не можна замінити або зрівноважити однією силою. Пара сил — самостійний об’єкт в статиці твердого тіла. Під час дії на тіло вона приводить до його обертання.
Площина, що визначається силами (  і
і  ), називається площиною дії пари, а відстань d між лініями дії сил — плечем пари.
), називається площиною дії пари, а відстань d між лініями дії сил — плечем пари.
5.2. Момент сили відносно точки. Нехай в точці А АТТ прикладена сила  . Виберемо довільну точку О, яка разом з силою
. Виберемо довільну точку О, яка разом з силою  визначає площину α. З точки О проведемо перпендикуляр на лінію дії сили (пряму АВ). Довжина цього перпендикуляра h називається плечем сили
визначає площину α. З точки О проведемо перпендикуляр на лінію дії сили (пряму АВ). Довжина цього перпендикуляра h називається плечем сили  відносно точки О (мал. 1.26).
відносно точки О (мал. 1.26).
 Моментом сили
Моментом сили  відносно О (М0(
відносно О (М0(  )) називається число із знаком, що дорівнює добутку величини сили на плече
)) називається число із знаком, що дорівнює добутку величини сили на плече
 (1.14)
(1.14)
Момент сили відносно точки вважаємо додатнім, якщо сила  обертає площину α навколо точки О проти годинникової стрілки (правило гвинта). Якщо обертання відбувається за годинниковою стрілкою, то момент — від’ємний.
обертає площину α навколо точки О проти годинникової стрілки (правило гвинта). Якщо обертання відбувається за годинниковою стрілкою, то момент — від’ємний.
Із означення момента сили відносно точки випливає:
1) Момент сили відносно точки дорівнює нулю тоді, і тільки тоді, коли лінія дії сили  проходить через точку О (h=0).
проходить через точку О (h=0).
2) Величина момента сили відносно точки дорівнює подвоєній площі трикутника, що визначається силою  і точкою О.
і точкою О.
Оскільки висота трикутника ОАВ не зміниться при переміщенні сили  по прямій АВ, то обертальний ефект від момента сили буде залежати від її величини, напрямку і плеча. Вимірюється момент сили відносно точки в ньютоно-метрах (Н*м).
по прямій АВ, то обертальний ефект від момента сили буде залежати від її величини, напрямку і плеча. Вимірюється момент сили відносно точки в ньютоно-метрах (Н*м).
За допомогою поняття момента сили відносно точки зручніше визначати точку С прикладання системи двох паралельних сил. Враховуючи (1.14), ліві частини рівностей (1.11) і (1.13) можна подати у вигляді
 (1.15)
(1.15)
Отже, точка прикладання рівнодійної системи двох паралельних сил визначається з умови перетворення в нуль суми моментів цих сил відносно шуканої точки. Рівність (1.15) являє собою окремий випадок відомої теореми Варіньона: якщо система двох паралельних сил має рівнодійну, то її момент відносно будь-якої точки дорівнює сумі моментів складових сил відносно цієї точки.
Точне доведення теореми буде приведене при розгляді просторової системи сил.
5.3. Момент пари. Розглянемо пари сил  і
і  (
(  =
=  ), які діють в площині α (мал. 1.27). оскільки пара сил, прикладена до твердого тіла, викликає обертальний ефект, то для оцінки його величини необхідно ввести кількісну характеристику пари. Виберемо в площини довільну точку О і обчислимо відносно неї суму моментів сил пари.
), які діють в площині α (мал. 1.27). оскільки пара сил, прикладена до твердого тіла, викликає обертальний ефект, то для оцінки його величини необхідно ввести кількісну характеристику пари. Виберемо в площини довільну точку О і обчислимо відносно неї суму моментів сил пари.

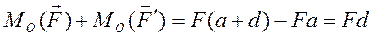 (1.16)
(1.16)
Остання рівність показує, що сума моментів сил пари відносно довільної точки площини α є величина постійна і не залежить від вибору точки. Цю величину приймемо за кількісну характеристику пари сил і назвемо моментом пари 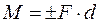 .
.
 Моментом пари будемо називати число зі знаком, яке дорівнює добутку однієї із сил пари на плече. Знак момента пари вибирається за правилом гвинта (рух площини дії пари проти годинникової стрілки). На мал. 1.27 пара
Моментом пари будемо називати число зі знаком, яке дорівнює добутку однієї із сил пари на плече. Знак момента пари вибирається за правилом гвинта (рух площини дії пари проти годинникової стрілки). На мал. 1.27 пара  і
і  має додатковий момент. Момент пари вимірюється в тих же одиницях, що і момент сили відносно точки (Н*м).
має додатковий момент. Момент пари вимірюється в тих же одиницях, що і момент сили відносно точки (Н*м).
5.4. Еквівалентність пар. Доведемо теорему, яка разом з наслідками, що випливають з неї, визначає основні властивості пар на площині.
Теорема: Дві пари, що діють в одній площині і мають однакові моменти, еквівалентні.
Доведення. Для доведення теореми необхідно показати, що одну пару можна перетворити в другу при допомозі додавання і розкладання сил.
Розглянемо дві пари сил  і
і  ,
,  і
і  , причому сили
, причому сили  і
і  непаралельні. (мал. 1.28). Знаходимо точку перетину відповідних ліній дії сил пар. В точці А перенесемо силу
непаралельні. (мал. 1.28). Знаходимо точку перетину відповідних ліній дії сил пар. В точці А перенесемо силу  , а в точку В — силу
, а в точку В — силу  . Розкладемо ці сили по напрямках АВ і ВD.
. Розкладемо ці сили по напрямках АВ і ВD.

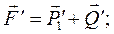 (1.17)
(1.17)
Оскільки сили  і
і  зрівноважені, то їх можна відкинути.
зрівноважені, то їх можна відкинути.
Таким чином, пара (  ,
,  ) перетворена в еквівалентну їй пару (
) перетворена в еквівалентну їй пару ( 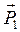 ,
,  ). Момент цієї пари, згідно теореми Варіньона, дорівнює
). Момент цієї пари, згідно теореми Варіньона, дорівнює
 (1.18)
(1.18)
Пари (  ) і (
) і (  ) мають однакові моменти
) мають однакові моменти  . Тому Р1=Р. Теорема доведена. У випадку паралельності сил
. Тому Р1=Р. Теорема доведена. У випадку паралельності сил  і
і  , для доведення теореми слід використовувати правила додавання і розкладання паралельних сил. Із доведеної теореми дістаємо такі властивості сил на площині:
, для доведення теореми слід використовувати правила додавання і розкладання паралельних сил. Із доведеної теореми дістаємо такі властивості сил на площині:
1. не змінюючи вплив на тіло, пару сил можна довільно переміщати в площині її дії;
 2. в заданій парі можна довільно змінювати величину сил або плече, залишаючи незмінним її момент, при цьому дія пари на тіло не змінюється.
2. в заданій парі можна довільно змінювати величину сил або плече, залишаючи незмінним її момент, при цьому дія пари на тіло не змінюється.
Звідси випливає, що дія пари на тверде тіло характеризується лише її моментом. Тому, особливо в техніці, пару сил зображують круговою стрілкою, яка вказує напрямок повороту, не зображаючи самі сили. На мал. 1.29 показано, що на тіло діє сила  і пара з моментом m.
і пара з моментом m.
5.5. Додавання пар, розміщених в одній площині. Умови рівноваги системи пар.
 Теорема: система пар, розміщених в одній площині еквівалентна одній парі, що діє в тій же площині, момент якої дорівнює алгебраїчній сумі моментів складових пар.
Теорема: система пар, розміщених в одній площині еквівалентна одній парі, що діє в тій же площині, момент якої дорівнює алгебраїчній сумі моментів складових пар.
Доведення. Допустимо, для спрощення доведення, що на тверде тіло в одній площині діє три пари з моментами m1, m2, m3 (мал. 1.30). На підставі попередньої теореми замінимо задані пари трьома парами з спільним плечем АВ=d і тими ж самими моментами

З останніх рівностей сили  ,
, 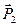 ,
,  визначаються однозначно. Додавши окремо, прикладені в точках А і В, матимемо в точці В силу
визначаються однозначно. Додавши окремо, прикладені в точках А і В, матимемо в точці В силу  , а в точці А — силу
, а в точці А — силу 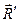 , які за величиною дорівнюватимуть
, які за величиною дорівнюватимуть

Це означає, що систему трьох пар ми замінили однією парою (  ,
, 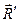 ) з моментом
) з моментом  . Такий же результат ми дістанемо при довільному числі пар. Теорема доведена.
. Такий же результат ми дістанемо при довільному числі пар. Теорема доведена.
Таким чином, розв’язок першої задачі статистики для системи пар на площині може бути сформульований так: довільна система пар на площині може бути зведена до однієї пари, момент якої дорівнює алгебраїчній сумі моментів складових пар
 (1.19)
(1.19)
Із доведеної теореми випливає, що для рівноваги системи пар на площині необхідно і достатньо, щоб алгебраїчна сума моментів цих пар дорівнювала нулю
 (1.20)
(1.20)
Співвідношення (1.20) виражає собою розв’язок другої задачі статики для системи пар на площині. За механічним змістом умова (1.20) забезпечує відсутність обертання твердого тіла в площині дії пар.
 Приклад 2. На горизонтальну балку АВ довжиною l діє пара сил з моментом m1. Визначити реакції опори, якщо ліва опора А являє собою нерухомий шарнір, а права опора В — рухомий циліндричний каток (мал.1.31).
Приклад 2. На горизонтальну балку АВ довжиною l діє пара сил з моментом m1. Визначити реакції опори, якщо ліва опора А являє собою нерухомий шарнір, а права опора В — рухомий циліндричний каток (мал.1.31).
Розв'язування. Опора В шарнірно рухома, тому реакція  направлена перпендикулярно до площини руху катка. Напрямок реакції
направлена перпендикулярно до площини руху катка. Напрямок реакції 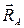 невизначений. Оскільки зовнішню пару сил можна зрівноважити тільки парою, то реакції
невизначений. Оскільки зовнішню пару сил можна зрівноважити тільки парою, то реакції 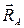 і
і  повинні утворювати пару сил
повинні утворювати пару сил  . Запишемо умову рівноваги системи пар:
. Запишемо умову рівноваги системи пар: 
З даної рівності знаходимо
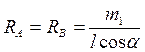
§6. Плоска система сил.
Якщо всі сили, що діють на тверде тіло, розміщені в одній площині, то така система сил називається плоскою. Оскільки нам відомі алгоритми знаходження рівнодійної системи збіжних сил і системи двох паралельних сил, то при розв’язку першої задачі статики для плоскої системи сил необхідно знайти метод її зведення до одного центра. Такий метод визначає теорема: силу, прикладену до абсолютно твердого тіла, можна, не змінюючи тіло, перенести паралельно їй самій в довільну точку тіла, додаючи при цьому пару сил з моментом, рівним моменту заданої сили відносно нової точки прикладання.
 Доведення. Нехай, сила
Доведення. Нехай, сила 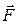 прикладена в точці А твердого тіла (мал. 1.32а).
прикладена в точці А твердого тіла (мал. 1.32а).
Виберемо довільну точку В і прикладемо в ній зрівноважену систему сил (  ,
,  ) таких, що
) таких, що  =
= 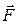 . Здобута система трьох сил являє собою силу
. Здобута система трьох сил являє собою силу  , прикладену в точці В, і пару сил (
, прикладену в точці В, і пару сил ( 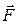 ,
,  ) з моментом m=MB(
) з моментом m=MB( 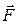 ). Отриманий результат можна зобразити так, як показано на мал.1.32б. (силу
). Отриманий результат можна зобразити так, як показано на мал.1.32б. (силу 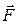 на цьому малюнку слід вважати відкинутою).
на цьому малюнку слід вважати відкинутою).
6.1. Зведення плоскої системи сил до найпростішого виду. Нехай на тверде тіло діє система сил  ,
,  ,....,
,....,  , розміщених в одній площині і прикладених відповідно в точках А1, А2,....., Аn. Виберемо на цій площині довільно точку О, яку назвемо центром зведення. Використовуючи теорему про паралельне перенесення сили, зведемо всі задані сили в точку О. В результаті цього на тіло буде діяти збіжна система сил
, розміщених в одній площині і прикладених відповідно в точках А1, А2,....., Аn. Виберемо на цій площині довільно точку О, яку назвемо центром зведення. Використовуючи теорему про паралельне перенесення сили, зведемо всі задані сили в точку О. В результаті цього на тіло буде діяти збіжна система сил 
з центром в точці О і система пар з моментами (мал. 1.33).
m1=MO(  ), m2=MO(
), m2=MO(  ),…, mn=MO(
),…, mn=MO(  ).
).
Збіжну систему сил замінимо однією силою
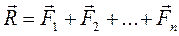 , (1.21)
, (1.21)
 а систему пар однією парою, момент якої визначається рівністю
а систему пар однією парою, момент якої визначається рівністю  (1.22)
(1.22)
Величина  дорівнює геометричній сумі всіх сил системи і називається головним вектором; величина МО — головним моментом системи сил. Головний момент дорівнює сумі моментів всіх заданих сил відносно центра О.
дорівнює геометричній сумі всіх сил системи і називається головним вектором; величина МО — головним моментом системи сил. Головний момент дорівнює сумі моментів всіх заданих сил відносно центра О.
Виходячи з вищесказаного, розв’язок першої задачі статики для плоскої системи сил подаємо так: довільна плоска система сил, що діє на АТТ, може бути зведена до однієї сили (головного вектора) і однієї пари (головного момента).
Відзначимо, що головний вектор  не залежить від вибору центра і може бути знайдений за формулою (1.21) аналітично або геометрично побудовою силового многокутника. Величини МО визначається формулою (1.22) і залежить від вибору точки О. Приведений вище метод зведення плоскої системи сил до одного центра називається методом Пуансон.
не залежить від вибору центра і може бути знайдений за формулою (1.21) аналітично або геометрично побудовою силового многокутника. Величини МО визначається формулою (1.22) і залежить від вибору точки О. Приведений вище метод зведення плоскої системи сил до одного центра називається методом Пуансон.
Розглянемо часткові випадки розв’язку першої задачі статики для плоскої системи сил.
1. 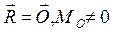 . Так як
. Так як 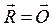 , то силовий многокутник , побудований на заданих силах, замкнений. У цьому випадку задана система сил еквівалентна одній парі з моментом МО. Якщо змінити центр зведення на іншу точку О1, то момент МО1 рівнодійної пари знову дорівнює М0. Якщо допустити протилежне
, то силовий многокутник , побудований на заданих силах, замкнений. У цьому випадку задана система сил еквівалентна одній парі з моментом МО. Якщо змінити центр зведення на іншу точку О1, то момент МО1 рівнодійної пари знову дорівнює М0. Якщо допустити протилежне 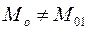 , то це означало б, що дві пари, еквівалентні одній і тій же системі сил, не еквівалентні між собою. А це неможливо.
, то це означало б, що дві пари, еквівалентні одній і тій же системі сил, не еквівалентні між собою. А це неможливо.
2.  . Це означає, що система сил еквівалентна одній силі
. Це означає, що система сил еквівалентна одній силі  , яка прикладена в точці О. цю систему тепер слід називати не результуючою, а рівнодійною. Отже, якщо головний вектор відмінний від нуля, а головний момент заданих сил відносно точки О дорівнює нулю, то система сил еквівалентна рівнодійній, лінія дії якої проходить через точку О. в даному випадку має місце теорема Варіньона:
, яка прикладена в точці О. цю систему тепер слід називати не результуючою, а рівнодійною. Отже, якщо головний вектор відмінний від нуля, а головний момент заданих сил відносно точки О дорівнює нулю, то система сил еквівалентна рівнодійній, лінія дії якої проходить через точку О. в даному випадку має місце теорема Варіньона:
Якщо плоска система сил має рівнодійну, то її момент відносно будь-якої точки дорівнює алгебраїчній сумі моментів усіх сил заданої системи відносно цієї точки.
 (1.23)
(1.23)
Точне доведення даної теореми буде приведено при вивченні просторової системи сил.
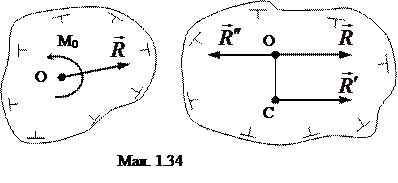 3.
3.  . В цьому випадку пару з моментом М0 можна зобразити двома силами
. В цьому випадку пару з моментом М0 можна зобразити двома силами  і
і  , вибираючи
, вибираючи  =
=  , а
, а  =-
=-  (мал. 1.34). При цьому повинна виконуватись умова
(мал. 1.34). При цьому повинна виконуватись умова
 (1.24)
(1.24)
Відкинувши зрівноважену систему сил (  ,
,  ), знаходимо, що система сил замінена однією рівнодійною
), знаходимо, що система сил замінена однією рівнодійною  =
=  , яка проходить через точку С. Її положення однозначно визначається рівністю (1.24) і знаком момента М0.
, яка проходить через точку С. Її положення однозначно визначається рівністю (1.24) і знаком момента М0.
Розглянуті випадки показують, що довільна плоска система сил, яка не перебуває у рівновазі, може бути зведена до однієї сили (рівнодійної), або однієї пари.
6.2. Умови рівноваги плоскої системи сил. Для рівноваги плоскої системи сил необхідно і достатньо, щоб одночасно виконувалися умови
 (1.25)
(1.25)
Враховуючи рівності (1.21), (1.22) і властивості проекцій сил на координатні осі, дістанемо
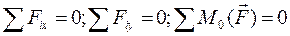 (1.26)
(1.26)
Рівності (1.26) виражають алгебраїчні умови рівноваги в основній формі: для рівноваги довільної плоскої системи необхідно і достатньо, щоб суми проекцій всіх сил на координатні осі і сума їх моментів відносно будь-якого центра, розміщеного в площині дії сил, дорівнювали нулю. По механічному змісту перші дві умови (1.26) виражають відсутність переміщень твердого тіла вздовж координатних осей, а третя — відсутність обертання в площині дії сил.
Крім основної форми рівноваги (1.26) на практиці широко використовуються і інші, еквівалентні основній, форми рівноваги плоскої системи сил, які ми приводимо без доведення.
Друга форма умов рівноваги: для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб суми моментів всіх сил відносно будь-яких двох різних точок А, В і сума їх проекцій на вісь х, не перпендикулярну до АВ, дорівнювали нулю
 (1.27)
(1.27)
Третя форма умов рівноваги: для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб суми моментів відносно будь-яких трьох не колінеарних точок А, В, і С дорівнювали нулю:
 (1.28)
(1.28)
 Із умов (1.26) — (1.27) можна одержати відповідні умови рівноваги системи паралельних сил на площині. Якщо допустити, що всі сили, які діють на тіло, паралельні осі У (мал. 1.35), то перша рівність в (1.26) і остання в (1.27) перетворяться в тотожності виду
Із умов (1.26) — (1.27) можна одержати відповідні умови рівноваги системи паралельних сил на площині. Якщо допустити, що всі сили, які діють на тіло, паралельні осі У (мал. 1.35), то перша рівність в (1.26) і остання в (1.27) перетворяться в тотожності виду  . В результаті умови рівноваги системи паралельних сил приймуть вид:
. В результаті умови рівноваги системи паралельних сил приймуть вид:
Основна форма умов рівноваги:
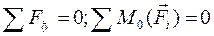 (1.29)
(1.29)
Друга форма умов рівноваги
 (1.30)
(1.30)
При цьому точки А і В не повинні належати прямій, паралельній силам.
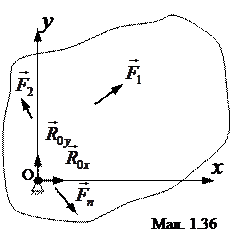 Умови рівноваги важеля. Важелем будемо називати тверде тіло, яке може обертатися навколо нерухомої осі під дією сил
Умови рівноваги важеля. Важелем будемо називати тверде тіло, яке може обертатися навколо нерухомої осі під дією сил  ,
,  ,....,
,....,  , розміщених в площині, перпендикулярній осі обертання (мал. 1.36).
, розміщених в площині, перпендикулярній осі обертання (мал. 1.36).
Найпростішими є важелі першого і другого роду. Розглядаючи рівновагу важеля, додамо до заданих сил складові реакцій циліндричного шарніра  і
і 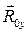 . Умови рівноваги плоскої системи сил виду (1.26) приймуть вигляд
. Умови рівноваги плоскої системи сил виду (1.26) приймуть вигляд
 (1.31)
(1.31)
Перші дві рівності (1.31) служать для визначення реакцій 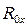 ,
,  , а остання не містить невідомих сил, тому є умовою рівноваги важеля.
, а остання не містить невідомих сил, тому є умовою рівноваги важеля.
6.2. Рівновага системи твердих тіл. Статичний розрахунок інженерних споруд в багатьох випадках зводиться до розгляду умов рівноваги конструкції, яка складається із системи твердих тіл, з’єднаних між собою певними в’язами, які ми будемо називати внутрішніми. Ці в’язі є складовими частинами конструкції. Метод розв’язку таких задач полягає в тому, що конструкцію розчленяють на окремі тіла і складають умови рівноваги для кожного з них, розглядаючи їх як вільні. При цьому реакції внутрішніх в’язей будуть попарно рівні по величині і протилежні за напрямком.
 Приклад 3. Кронштейн складається із двох стержнів АВ і ВС, з’єднаних в точці В і прикріплених до вертикальної стінки в точках А, С шарнірно. Вага стержня АВ-Р1=150Н, а стержня ВС-Р2=120Н. в точці В прикладена сила Р=300Н. розміри показані на малюнку. Визначити реакції шарнірів А і С, вважаючи стержні однорідними (мал. 1.37).
Приклад 3. Кронштейн складається із двох стержнів АВ і ВС, з’єднаних в точці В і прикріплених до вертикальної стінки в точках А, С шарнірно. Вага стержня АВ-Р1=150Н, а стержня ВС-Р2=120Н. в точці В прикладена сила Р=300Н. розміри показані на малюнку. Визначити реакції шарнірів А і С, вважаючи стержні однорідними (мал. 1.37).
Розв’язування. Відкинемо в’язі, замінивши їх дію невідомими реакціям, і розглянемо рівновагу кронштейна в цілому під дією сил  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 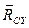 .
.
Запишемо умови рівноваги плоскої системи сил
 ;
;  ;
;
 .
.
Отримані три рівняння містять чотири невідомих  ,
,  ,
, 123Следующая ⇒