Главная | Обратная связь

Единицы электродвижущей силы

За единицу электродвижущей силы принимают такую электродвижущую силу, которая способна поддерживать в проводнике с сопротивлением в 1 ом силу тока, равную 1 амперу. Эта единица носит название – вольт. Одна тысячная доля вольта носит название милливольт.

Сопротивление компонента электрической цепи или проводника — величина, характеризующая степень его противодействия электрическому току. Сопротивление определяется как отношение разности потенциалов к силе тока. Единицей сопротивления служит ом (Ом). Сопротивление в 1 Ом имеет проводник, по которому течет ток силой 1 А при разности потенциалов 1 В.

Разность потенциалов между двумя точками стационарного электрического или гравитационного поля измеряется работой, совершаемой силами поля при перемещении единичного положительного заряда или, соответственно, единичной массы из одной точки с большим потенциалом в другую с меньшим потенциалом. Если j₁, j₂ — потенциалы начальной и конечной точек траектории перемещаемого заряда (или массы), то Р. п. u = j₁—j₂; изменение потенциала Dj= j₂—j₁ =—и.

Работа произвольного электрического поля по перемещению +1 заряда из одной точки в другую называемый электрическим напряжением между этими точками; в случае стационарного поля напряжение совпадает с Р. п.

Сопротивление R однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины и сечения следующим образом:

где ρ — удельное сопротивление вещества проводника, L — длина проводника, а S — площадь сечения. Величина, обратная удельному сопротивлению называется удельной проводимостью. Эта величина связана с температурой формулой Нернст-Эйнштейна:

где

· T — температура проводника;

· D — коэффициент диффузии носителей заряда;

· Z — количество электрических зарядов носителя;

· e — элементарный электрический заряд;

· C — Концентрация носителей заряда;

· — постоянная Больцмана.

Следовательно, сопротивление проводника связано с температурой следующим соотношением:

Сопротивление также может зависеть от параметров 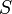и , поскольку сечение и длина проводника также зависят от температуры.

Сверхпроводи́мость — свойство некоторых материалов обладать строго нулевым электрическим сопротивлением при достижении ими температуры ниже определённого значения (критическая температура). Известны несколько десятков чистых элементов, сплавов и керамик, переходящих в сверхпроводящее состояние. Сверхпроводимость — квантовое явление. Оно характеризуется также эффектом Мейснера, заключающимся в полном вытеснении магнитного поля из объема сверхпроводника. Существование этого эффекта показывает, что сверхпроводимость не может быть описана просто как идеальная проводимость в классическом понимании.

Открытие в 1986—1993 гг. ряда высокотемпературных сверхпроводников (ВТСП) далеко отодвинуло температурную границу сверхпроводимости и позволило практически использовать сверхпроводящие материалы не только при температуре жидкого гелия (4.2 К), но и при температуре кипения жидкого азота (77 К), гораздо более дешевой криогенной жидкости.

будет фазовым переходом ΙΙ рода.

Эффект Мейснера

Основная статья: Эффект Мейснера

Даже более важным свойством сверхпроводника, чем нулевое электрическое сопротивление, является так называемый эффект Мейснера, заключающийся в выталкивании сверхпроводником магнитного потока . Из этого экспериментального наблюдения делается вывод о существовании незатухающих токов внутри сверхпроводника, которые создают внутреннее магнитное поле, противоположно направленное внешнему, приложенному магнитному полю и компенсирующее его.

Достаточно сильное магнитное поле при данной температуре разрушает сверхпроводящее состояние вещества. Магнитное поле с напряжённостью Н_c, которое при данной температуре вызывает переход вещества из сверхпроводящего состояния в нормальное, называется критическим полем. При уменьшении температуры сверхпроводника величина Н_c возрастает. Зависимость величины критического поля от температуры с хорошей точностью описывается выражением

,

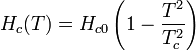где 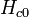— критическое поле при нулевой температуре. Сверхпроводимость исчезает и при пропускании через сверхпроводник электрического тока с плотностью, большей, чем критическая 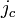, поскольку он создаёт магнитное поле, большее критического.

[править] Эффект Литтла-Паркса

В 1962 году учёными Литтлом и Парксом было обнаружено, что температура перехода тонкостенного цилиндра малого радиуса в сверхпроводящее состояние периодически (с периодом равным кванту потока) зависит от величины магнитного потока.^[6] Этот эффект является одним из проявлений макроскопической квантовой природы сверхпроводимости.

 

49.Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей. В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 4.10.1). Токи, втекающие в узел, принято считать положительными; токи, вытекающие из узла – отрицательными.

1

Рисунок 4.10.1. Узел электрической цепи. I1, I2 > 0; I3, I4 < 0

В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа: Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:

I1 + I2 + I3 + ... + In = 0.

Первое правило Кирхгофа является следствием закона сохранения электрического заряда. В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи. На рис. 4.10.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).

2

Рисунок 4.10.2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef).

В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков. Второе правило Кирхгофа является следствием обобщенного закона Ома. Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 4.10.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 4.10.3.

3

Рисунок 4.10.3. «Правила знаков».

Для участков контура abcd обобщенный закон Ома записывается в виде: Для участка bc: I1R1 = Δφbc – 1. Для участка da: I2R2 = Δφda – 2. Складывая левые и правые части этих равенств и принимая во внимание, что Δφbc = – Δφda , получим:

I1R1 + I2R2 = Δφbc + Δφda – 1 + 2 = – 1 – 2.

Аналогично, для контура adef можно записать:

– I2R2 + I3R3 = 2 + 3.

Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура. Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета электрической цепи. Для цепи, изображенной на рис. 4.10.2, система уравнений для определения трех неизвестных токов I1, I2 и I3 имеет вид:

I1R1 + I2R2 = – 1 – 2,

 

– I2R2 + I3R3 = 2 + 3,

 

– I1 + I2 + I3 = 0.

Таким образом, правила Кирхгофа сводят расчет разветвленной электрической цепи к решению системы линейных алгебраических уравнений. Это решение не вызывает принципиальных затруднений, однако, бывает весьма громоздким даже в случае достаточно простых цепей. Если в результате решения сила тока на каком-то участке оказывается отрицательной, то это означает, что ток на этом участке идет в направлении, противоположном выбранному положительному направлению

50.Электроны проводимости в металле находятся в беспорядочном движении. Наиболее быстро движущиеся электроны, обладающие достаточно большей кинетической энергией, могут вырываться из металла в окружающее пространство. При этом они совершают работу как против сил притяжения со стороны избыточного положительного заряда, возникающего в металле в результате их вылета, так и против сил отталкивания со стороны ранее вылетевших электронов, образующих вблизи поверхности проводника электронное “облако”. Между электронным газом, в металле и электронным «облаком” устанавливается динамическое равновесие. Работу, которую нужно совершить для удаления электрона из металла в вакуум называют работой выхода. Она равна , где е -заряд электрона, - потенциал выхода. Работа выхода производится электронами - за счет уменьшения их кинетической энергии. Поэтому понятно, что медленно движущиеся электроны вырваться из металла не могут. Работа выхода зависит от химической природы металла и состояния его поверхности загрязнения, следы влаги и пр. изменяют ее величину. Для чистых металлов работа выхода колеблется в пределах нескольких электронвольт. Электрон проводимости может вылететь из какого либо металла в том случае, если его энергия превышает работу выхода А электрона из металла. Явление испускания электронов нагретыми металлами называется термоэлектронной эмиссией.

Концентрация 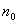электронов проводимости в металле весьма велика; их тепловые скорости при данной температуре различны и распределены, по классическим представлениям, в соответствии с законом Максвелла. Это означает, что даже при средних температурах в металле имеется достаточно большое число электронов проводимости, способных совершить работу выхода и вылететь из металла. При этом работа выхода равна убыли кинетической энергии

где m, е - соответственно масса и заряд электрона, и - скорости электрона до и после выхода из металла. При обычных температурах количество электронов, имеющих скорость, достаточную для вылета, очень невелика. Существуют несколько способов сообщения электронам дополнительной энергии, необходимой для удаления их из металла: нагревание проводника (термоэлектронная эмиссия); облучение металлов видимым и ультрафиолетовым светом (фотоэлектронная эмиссия); воздействие ускоряющего внешнего электрического поля (автоэлектронная, или холодная эмиссия); бомбардировка металла электронами или ионами.

Для того чтобы получить значительный поток электронов, так называемый эмиттер нагревают до температур порядка 2000÷2500 К.

Контактная разность потенциалов — это разность потенциалов, возникающая при соприкосновении двух различных проводников, имеющих одинаковую температуру.

При соприкосновении двух проводников с разными работами выхода на проводниках появляются электрические заряды. А между их свободными концами возникает разность потенциалов. Разность потенциалов между точками находящимися вне проводников, в близи их поверхности называется контактной разностью потенциалов^[1]. Так как проводники находятся при одинаковой температуре, то в отсутствие приложенного напряжения поле может существовать только в пограничных слоях (Правило Вольта). Выделяется внутренняя разность потенциалов(при соприкосновении металлов) и внешняя (в зазоре). Значение внешней контактной разности потенциалов равно разности работ выхода отнесенной к заряду электрона. Если проводники соединить в кольцо то ЭДС в кольце будет равна 0. Для разных пар металлов значение контактной разности потенциалов колеблется от десятых до единиц вольт.^[2]

Электрич. поле К. р. п., создаваемое приконтактным объёмным зарядом, сосредоточено вблизи границы раздела и в зазоре между проводниками. Протяжённость приконтактной области тем меньше, чем больше концентрации электронов проводимости в проводниках: в металлах см, в полупроводниках до см. При контакте полупроводника с металлом практически вся область приконтактного поля локализована в полупроводнике.

Вольт (В, V) может быть определён либо как электрическое напряжение на концах проводника, необходимое для выделения в нём тепла мощностью в один ватт (Вт, W) при силе протекающего через этот проводник постоянного тока в один ампер (A), либо как разность потенциалов между двумя точками электростатического поля, при прохождении которой над зарядом величиной 1 кулон (Кл, C) совершается работа величиной 1 джоуль (Дж, J)^[2]. Выраженный через основные единицы системы СИ, один вольт равен м² · кг · с⁻³ · A⁻¹.

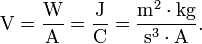
Вольт (русское обозначение: В; международное: V) — в Международной системе единиц (СИ) единица измерения электрического потенциала, разности потенциалов, электрического напряжения и электродвижущей силы.

Разность потенциалов между двумя точками равна 1 вольту, если для перемещения заряда величиной 1 кулон из одной точки в другую над ним надо совершить работу величиной 1 джоуль. Вольт также равен электрическому напряжению, вызывающему в электрической цепи постоянный ток силой 1 ампер при мощности 1 ватт.

Единица названа в честь итальянского физика и физиолога Алессандро Вольта (1745–1827), который изобрёл вольтов столб, первую электрическую батарею.

1 В = (1/300) ед. потенциала СГСЭ^[1].