 |
|
Лабораторная работа № 1. Линейные вычислительные процессы
Задание 1. Дано вещественное число A. Не пользуясь никакими другими арифметическими операциями, кроме умножения, получить A10 за 4 операции.
Задание 2. Даны три вещественных числа А, В и С. Разработать программу обмена значениями этих величин по следующей схеме: В присвоить значение С, А присвоить значение В, С присвоить значение А.
Задание 3. Разработать программу для вычисления суммы цифр заданного трехзначного целого числа.
Задание 4. Разработать программу для решения задачи своего варианта
Варианты задания
1. Вычислить полную поверхность пирамиды, в основании которой лежит квадрат со стороной b. Высота пирамиды h.
2. Вычислить объем пирамиды, в основании которой лежит квадрат со стороной b. Высота пирамиды h.
3. Вычислить объем пирамиды, в основании которой лежит равносторонний треугольник со стороной b. Высота пирамиды h.
4. Вычислить площадь треугольника по двум сторонам а, b и углу α между ними.
5. Вычислить объем и полную поверхность цилиндра. Высота цилиндра h, радиус основания r.
6. Вычислить объем прямой призмы, в основании которой лежит прямоугольный треугольник с катетами а и b. Высота призмы h.
7. Вычислить полную поверхность прямой призмы, в основании которой лежит квадрат со стороной b. Высота призмы h.
8. Вычислить полную поверхность прямой призмы, в основании которой лежит равносторонний треугольник со стороной b. Высота призмы h.
9. Вычислить объем прямой призмы, в основании которой лежит квадрат со стороной b. Высота призмы h.
10. Вычислить объем прямой призмы, в основании которой лежит равносторонний треугольник со стороной а. Высота призмы h.
11. Вычислить объем и полную поверхность куба, ребро которого b.
12. Вычислить площадь кольца, внутренний диаметр которого d, a внешний D.
13. Вычислить поверхность сферы и объем шара. Радиус шара r.
14. Вычислить полную поверхность прямой призмы, в основании которой лежит прямоугольный треугольник с катетами а и b. Высота призмы h.
15. Вычислить объем цилиндрической трубы со стенками толщиной t. Внешний диаметр d, высота трубы h.
Задание 5.Разработать программу для решения задачи своего варианта. В задании необходимо вычислить результат по приведенной формуле и вывести на экран исходные данные и результат в указанном формате. Сверить полученный результат с ответом.
Варианты задания
1. 
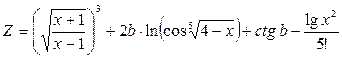при х = 3,8; b =-4,82
Вывести результат с 2-мя цифрами в дробной части. Ответ: 5.13
2. 
при х = 0,85
Вывести результат с 3-мя цифрами в дробной части. Ответ: 4.844
3. 
при а = 0,83; b = 4,66
Вывести результат с 3-мя цифрами в дробной части. Ответ: 6.028
4. 
при х =4,47; а = 3
Вывести результат с 2-мя цифрами в дробной части. Ответ: 1002.15
5. 
при х=1,15; а =3,71; у=0,89
Вывести результат с 5-ю цифрами в дробной части. Ответ: -0.29615
6. 
при х = -0,17; z =3,81
Вывести результат с 2-мя цифрами в дробной части. Ответ: 26414.26
7. 
при а = 0,672
Вывести результат с 3-мя цифрами в дробной части. Ответ: 1.896
8. 
при х = 0,85; у = 2,34
Вывести результат с 3-мя цифрами в дробной части. Ответ: 10.736
9. 
при а = 0,53; b = 1,87
Вывести результат с 3-мя цифрами в дробной части. Ответ: -1.265
10. 
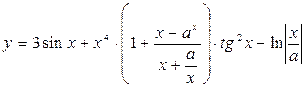при х = - 0,25; а = 0,31
Вывести результат с 4-мя цифрами в дробной части. Ответ: -0.5266
11. 
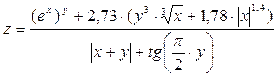при х = 1,25; у = -2,14
Вывести результат с 2-мя цифрами в дробной части. Ответ: -33.2
12. 
при а = 1,87
Вывести результат с 4-мя цифрами в дробной части. Ответ: 0.1367
13. 
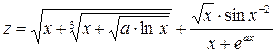при х = 3,89; а = 4,01
Вывести результат с 3-мя цифрами в дробной части. Ответ: 2.394
14. 
при х =0,97; а = 2,34
Вывести результат с 3-мя цифрами в дробной части. Ответ: 0.744
15. 
при х = 2,17; а = 0,11
Вывести результат с 2-мя цифрами в дробной части. Ответ: 71.44
Дополнительные задачи
1. Треугольник задан координатами своих вершин. Разработать программу для вычисления:
а) периметра треугольника;
б) площади треугольника;
в) углов треугольника;
г) длин высот треугольника;
д) длин медиан треугольника;
е) длин биссектрис треугольника;
ж) радиуса вписанной окружности;
з) радиуса описанной окружности.
2. Разработать программу для определения h — полного количества часов и m — полного количества минут, прошедших от начала суток до того момента (в первой половине дня), когда часовая стрелка повернулась на f градусов (0 £ f < 360).
Лабораторная работа № 2. Разветвляющиеся вычислительные
процессы
Задание 1. Определить максимальное и минимальное значения из трех различных вещественных чисел.
Задание 2.Ввести с клавиатуры 3 целых числа. Определить и выдать на экран те числа, которые попадают в диапазон от 2 до 5, лежат на границе и находятся вне указанного диапазона.
Задание 3.Дано целое число N (N ≤ 9999). Определить, является это ли это число палиндромом («перевертышем»), т.е. таким числом, десятичная запись которого читается одинаково слева направо и справа налево. Примеры палиндромов: 2222, 6116, 0440.
Задание 4.Дано целое число N (N ≤ 100), определяющее возраст человека в годах. Разработать программу для указания после этого числа слова «год», «года» или «лет». Например, 1 год, 12 лет, 53 года, и т.д.
Задание 5. Разработать программу для решения квадратного уравнения ax2 + bx +c=0 при любых вещественных значениях a, b, c. Проверить работу программы, проведя расчеты для пяти вариантов:
1) a = 2; b = ‑7; c = 5; 2) a = -2; b = 3; c = -7; 3) a = 0; b = 3; c = 1;
4) a = 0; b = 0; c = 2; 5) a = 0; b = 0; c = 0.
