 |
|
Лабораторная работа №7. Процедуры и функции
Задание 1.Написать функцию вычисления среднего арифметического и процедуру вычисления среднего гармонического в одномерном вещественном массиве. Ввести с клавиатуры три одномерных вещественных массива a1, a2, …, an , b1, b2, … , bm и c1, c2, …, ck. Вычислить и вывести на экран отношение среднего арифметического к среднему гармоническому для каждого массива, используя разработанные функцию и процедуру.
Указание. Среднее гармоническое вычисляется по формуле:
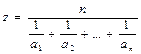
Задание 2. Разработать процедуру, вычисляющую с точностью e корень уравнения f(x)=0 на интервале [a,b] на основе дихотомического поиска (метод половинного деления), либо сообщает об отсутствии корня на указанном интервале. Разработать программу, которая использует указанную процедуру и вычисляет корень уравнения для двух функций f1(x) и f2(x) своего варианта.
| N варианта | f1(x) | f2(x) |
| x + lg x-0,5 | 
| |
| 3x – cos x – 1 | ex + ln x – 10x | |
| x × ex – 1 | 
| |
| 2x + cos x – 0,5 | 3x – 14 + ex – e -x | |
| 2 – x – ln x | sin x2 + cos x2 – 10 x | |
| sin(0,5 + x) – 2x + 0,5 | 0,6 × 3x -2,3x - 3 | |
| (x - 1)2 – 0,5ex |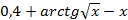 
| |
| 2x – lg x – 7 | 
| |
| x3 – 2 – ln(x + 2) | 
| |
| lg (1 + 2x) – 2 + x | 
| |
| x2 – 1 – ln (x + 1) | 
| |
| 2sin(x – 0,6) – 1,5 + x | 0,1x2 – x ×ln x | |
| ex – e-x – 2 | 
| |
| x2 – 2cos x + 1 | 
| |
| (2x – 3)2 – ex |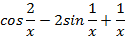 
|
Задание 3.Разработать процедуру вычисления определенного интеграла 
методом трапеций, разбивая интервал интегрирования на n частей. Вычислить два интеграла своего варианта, используя разработанную процедуру.
| N варианта | 1-й интеграл | 2-й интеграл |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
|
| 
|
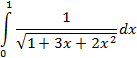
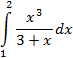
Задание 4. Разработать процедуру, результатом работы которой является истинное значение, если символ, передаваемый в процедуру, является буквой, и ложное значение в противном случае. В программе эту процедуру использовать в цикле и выдавать сообщение на экран о введенных символах (если введенный символ - буква, то сообщать true, не буква – false).
Задание 5. Разработать программу для решения задачи своего варианта.
Варианты задания
1. Описать функцию
и использовать ее для вычисления z = (sign x + sign y) · sign(x - y).
2. Описать функцию
и использовать ее для вычисления y = n!! + (n + 1)!! – (2n)!!.
3. Описать функцию Stepen(x,n) от вещественного х и целого n, вычисляющую через умножение величину xn, и использовать ее для вычисления b = 2.7k + (a + 1)-5.
4. Даны 3 квадратных уравнения ax2+ bx + c = 0, bx2+ ax + с = 0 и cx2+ ax + b = 0. Сколько из них имеют вещественные корни? Определить функцию, позволяющую распознавать наличие вещественных корней в квадратном уравнении.
5. Даны три целых трехзначных числа. Выяснить, в каком из них сумма цифр больше. Определить функцию для расчета суммы цифр в целом трехзначном числе.
6. Описать функцию для вычисления факториала числа n и использовать ее для вычисления z = (n!)! / (2n)!.
7. Определить функцию для расчета суммы цифр в целом трехзначном числе и использовать ее для вывода всех нечетных трехзначных чисел, сумма цифр которых равна m.
8. Заданы стороны треугольника a, b, c и углы A, B, C. Вычислить все медианы треугольника и вывести на печать значение наибольшей из них. Определить функцию для вычисления медианы треугольника. Указание. Медиана треугольника, проведенная к стороне а, вычисляется по формуле: 
.
9. Заданы стороны треугольника a, b, c. Найти медианы треугольника, сторонами которого являются медианы исходного треугольника. Указание. Медиана треугольника, проведенная к стороне а, вычисляется по формуле: 
.
10. Вычислить периметр четырехугольника, заданного координатами вершин. Определить функцию для расчета длины стороны. Указание. Длина стороны, заданной координатами вершин, вычисляется по формуле: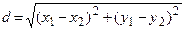 
.
11. Вычислить площадь треугольника, заданного координатами вершин. Определить функцию для расчета длины стороны по координатам вершин. См. указание к варианту 10.
12. Три точки на плоскости заданы своими координатами. Определить, какие из них находятся на максимальном расстоянии друг от друга. Вычисление расстояния между двумя точками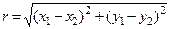 
оформить в виде функции.
13. Даны основания и высоты двух равнобедренных трапеций. Найти сумму их периметров. Определить функцию для расчета периметра равнобедренной трапеции.
14. Даны основания и высоты двух равнобедренных трапеций. Найти разность их площадей. Определить функцию для расчета площади равнобедренной трапеции.
15. Описать функцию для вычисления логарифма по произвольному основанию
logat = ln t /ln a и использовать ее для вычисления g=log2x –logc(x+y)/logc+1(x-y).
Задание 6. Разработать программу для решения задачи своего варианта.
Варианты задания
1. Заданы 3 вектора a1, a2, … , an, b1, b2, … , bm и c1, c2, … , ck. Вычислить длину каждого вектора. Вычисление длины вектора, ввод и вывод элементов массива оформить в виде процедур. Вывести на экран информацию о том, длина какого вектора больше. Указание. Длина вектора x1, x2, … , xn вычисляется по формуле
2. Заданы массивы a1, a2, … , an, b1, b2, … , bm и c1, c2, … , ck. В каждом массиве вычислить среднее арифметическое отрицательных элементов. Указанный подсчет, ввод и вывод элементов массива оформить в виде процедур. Вывести на экран информацию о том, в каком массиве значение среднего арифметического больше.
3. Заданы массивы a1, a2, … , an, b1, b2, … , bm и c1, c2, … , ck. Вычислить
z = (mina + minb + minc)/3, где mina, minb и minc – минимальные элементы массивов А, В и С. Поиск минимального элемента массива, ввод и вывод элементов массива оформить в виде процедур.
4. Заданы массивы a1, a2, … , an, b1, b2, … , bm и c1, c2, … , ck. Вычислить
q = (Sa+Sb+Sc)/(Ka·Kb·Kc), где Sa, Ka, Sb, Kb, Sc и Kc – сумма и количество положительных элементов массивов А, В и С. Вычисление суммы и количества положительных элементов массива, ввод и вывод элементов массива оформить в виде процедур.
5. Заданы 3 вектора a1, a2, … , an, b1, b2, … , bn и c1, c2, … , cn. Вычислить скалярные произведения АВ, АС и ВС и вывести на экран наибольшее из них. Вычисление скалярного произведения, ввод и вывод элементов массива оформить в виде процедур. Указание. Скалярное произведение 2-х векторов x1, x2, … , xn и y1, y2, …, yn вычисляется по формуле 
.
6. Заданы массивы a1, a2, … , an, b1, b2, … , bm и c1, c2, … , ck. В каждом массиве подсчитать среднее гармоническое элементов. Указанный подсчет, ввод и вывод элементов массива оформить в виде процедур. Вывести на экран информацию о том, в каком массиве среднее гармоническое больше. См. указание к Заданию 1.
7. Заданы массивы a1, a2, … , an, b1, b2, … , bm и c1, c2, … , ck. В каждом массиве подсчитать сумму элементов. Подсчет суммы, ввод и вывод элементов массива оформить в виде процедур. Вычислить
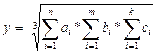
8. Заданы массивы a1, a2, … , an, b1, b2, … , bm и c1, c2, … , ck. В каждом массиве подсчитать среднее геометрическое положительных элементов. Указанный подсчет, ввод и вывод элементов массива оформить в виде процедур. Вывести на экран информацию о том, в каком массиве среднее геометрическое меньше.
Указание. Среднее геометрическое вычисляется по формуле: 
9. Заданы массивы a1, a2, … , an, b1, b2, …, bm и c1, c2, … , ck. В каждом массиве подсчитать количество положительных и количество отрицательных элементов. Указанный подсчет, ввод и вывод элементов массива оформить в виде процедур. Вывести на экран информацию о том, в каких массивах количество положительных элементов больше количества отрицательных элементов.
10. Заданы массивы a1, a2, … , an, b1, b2, … , bm и c1, c2, … , ck. В каждом массиве найти максимальный элемент и вывести их на экран в порядке возрастания. Поиск максимального элемента массива, ввод и вывод элементов массива оформить в виде процедур.
11. Заданы массивы a1, a2, … , an, b1, b2, … , bm и c1, c2, … , ck. В каждом массиве подсчитать сумму отрицательных элементов. Указанный подсчет, ввод и вывод элементов массива оформить в виде процедур. Вывести на экран информацию о том, в каком массиве сумма отрицательных элементов меньше.
12. Заданы целочисленные массивы a1, a2, … , an, b1, b2, … , bm и c1, c2, … , ck. В каждом массиве подсчитать произведение элементов, кратных трем. Указанный подсчет, ввод и вывод элементов массива оформить в виде процедур. Вывести на экран информацию о том, в каком массиве произведение элементов, кратных трем, больше.
13. Данные трех серий измерений заданы с помощью массивов a1, a2, … , an,
b1, b2, … , bm и c1, c2, … , ck. Вычислить математическое ожидание и среднеквадратическое отклонение каждой серии. Указанные вычисления, ввод и вывод элементов массива оформить в виде процедур. Вывести на экран информацию о том, в какой серии среднеквадратическое отклонение наименьшее. Указание. Математическое ожидание и среднеквадратическое отклонение серии x1, x2, … , xn вычисляется по формулам:
14. Заданы массивы a1, a2, … , an и b1, b2, … , bm. В каждом массиве найти максимальный элемент, а затем поменять их местами (максимальный элемент массива А поставить на место максимального элемента массива В, а максимальный элемент массива В поставить на место максимального элемента массива А). Поиск максимального элемента, ввод и вывод элементов массива оформить в виде процедуры.
15. Заданы массивы a1, a2, … , an, b1, b2, … , bm и c1, c2, … , ck. В каждом массиве заменить нулевые элементы полусуммой соседних элементов. Первый и последний элементы массива оставить без изменения. Указанную замену элементов, ввод и вывод элементов массива оформить в виде процедур.