 |
|
Потенциал. Электрическое напряжение
Закон Кулона. Напряженность электрического поля
Взаимодействие точечных заряженных тел описывается законом Кулона.
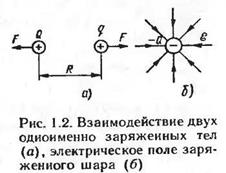
Сила взаимодействия F между точечными заряженными телами Q и q, расположенными в данной среде на расстоянии R друг от друга (рис. 1.2, а), прямо пропорциональна произведению зарядов этих тел и обратно пропорциональна квадрату расстояния между ними:
(1.1)
 |
где Q и q — значения зарядов, Кл (1 Кл = 6,3·1018 зарядов электрона);
— относительная диэлектрическая проницаемость среды, показывающая, во сколько раз сила взаимодействия в данной среде меньше, чем в вакууме (величина безразмерная); 
= 8,86 ·10-12 Ф/м — электрическая постоянная.
Рисунок 1.2 Взаимодействие двух одноименно заряженных тел (а), электрическое поле заряженного шара
Введем силовую характеристику поля — напряженность:
E=F/q .
Напряженность электрического поля в данной точке определяется силой, действующей на помещенное в эту точку пробное тело, обладающее единичным положительным зарядом.
Единица напряженности [E] = Н/Кл (ньютон на кулон).
Для поля уединенного точечного заряженного тела на основании закона Кулона
(1.2)
Рассмотрим в качестве примера электрическое поле уединенного заряженного металлического шара с зарядом — Q (рис. 1.2, б). Напряженность поля внутри металлического шара при статическом заряде равна нулю. В самом деле, при наличии электрического поля в проводящей среде электроны благодаря взаимному отталкиванию придут в движение и, следовательно, статическое состояние установится только тогда, когда напряженность поля внутри шара станет равной нулю. Таким образом, избыточный электрический заряд распределится только на его поверхности.
Напряженность поля вне шара и на его поверхности находят, предполагая, что заряд – Q сосредоточен в центре шара.
Потенциал. Электрическое напряжение
 |
Пусть уединенное неподвижное точечное заряженное тело с зарядом Q расположено в произвольной точке горизонтальной плоскости (рис. 1.3). Если в точке А окажется пробное заряженное тело с зарядом q, то под действием силы
оно станет перемещаться. При этом за счет энергии поля зарядов Q и q будет совершаться определенная работа. Поскольку сила 
непрерывно меняется, для нахождения работы, которую совершает поле, перемещая пробное заряженное тело из данной точки в бесконечность, разобьем путь на элементарные участки ΔR, так что в пределах каждого такого участка силу 
можно считать неизменной. Тогда элементарная работа этой силы 
Рисунок 1.3 К определению потенциала электрического поля
Для определения всей работы А необходимо просуммировать элементарные работы ΔА на участке пути от 
до бесконечности. Тогда 
. Точное значение этой работы
.
Работа выражается в джоулях (Дж).
Введем энергетическую характеристику поля - потенциал φ.
Потенциалом электрического поля заряда Q в данной точке называют величину, численно равную работе, которую совершает поле, перемещая пробное тело, обладающее единичным положительным зарядом, из данной точки в бесконечность:
(1.3)
Единица потенциала [φ] = 1 Дж/1 Кл = 1 В.
Потенциал данной точки поля равен I В, если при переносе пробного тела с зарядом в 1 Кл из данной точки в бесконечность совершается работа в 1 Дж.
В том случае, когда заряженное тело, создающее поле, имеет отрицательный заряд, поле будет препятствовать удалению пробного заряженного тела, т. е. потенциал поля будет отрицательным. Сопоставив формулы (1.2) и (1.3)„ видим, что
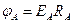(1.4)
откуда 
.
Единица напряженности поля [E]= В/м (вольт на метр).
Определив потенциал электрического заряда Q в точках А и В (рис. 1.4), найдем их разность, которую называют электрическим напряжением между двумя точками поля:
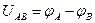(1.5)
 |
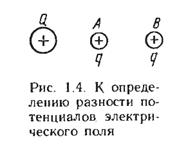Рисунок 1.4 К определению разности потенциалов электрического поля
Таким образом, электрическим напряжением или разностью потенциалов между двумя точками поля называют величину, численно равную работе, которую совершает поле, перемещая между этими точками пробное тело, обладающее единичным положительным зарядом
Выясним, как изменяется потенциал точек внутри и вне металлического шара с зарядом - Q. Так как избыточный заряд шара неподвижен и расположен на поверхности, разность потенциалов между внутренними точками шара и точками, расположенными на его поверхности, равна нулю. Следовательно, потенциалы всех точек шара равны потенциалу точек на его поверхности. Потенциал точек, расположенных на поверхности и вне шара, определяют из предположения, что весь заряд шара сосредоточен в его центре.
Электрические поля уединенного точечного заряженного тела и уединенного заряженного шара являются неоднородными, т. е. полями, у которых напряженность во всех точках различна. На практике часто приходится иметь дело с однородным полем, у которого напряженность во всех точках одинакова. Такое поле возникает, например, между двумя равномерно заряженными металлическими пластинами на достаточном удалении от их краев (рис. 1.5). При этом электрическое напряжение однородного поля
(1.6)
 |
Рисунок 1.5 Однородное электрическое поле