Главная | Обратная связь

ГЛАВА 2. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Электрическая цепь

Электрический ток

ЭДС и напряжение

Закон Ома

Рассмотрим участок цепи длиной l и площадью поперечного сечения S (рис. 2.2.).

Рисунок 2.2 Участок электрической цепи в виде отрезка металлического проводника

 

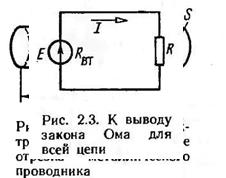
Рисунок 2.3 К выводу закона Ома для всей цепи

 

Пусть проводник находится в однородном электрическом поле напряженностью E=U/l. Под действием этого поля свободные электроны проводника совершают ускоренное движение в направлении, противоположном вектору E. Движение электронов происходит до тех пор, пока они не столкнутся с ионами кристаллической решетки проводника. При этом скорость электронов падает до нуля, после чего процесс ускорения электронов повторяется снова. Так как движение электронов равноускоренное, то их средняя скорость

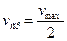(2.7)

где - скорость электронов перед столкновением с ионами.

Очевидно, что скорость (прямо пропорциональна напряженности поля E; следовательно, и средняя скорость пропорциональна E. Но ток и плотность тока определяются скоростью движения электронов в проводнике. Таким образом,

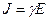(2.8)

Это выражение является дифференциальной формой закона Ома.

Коэффициент пропорциональности γ называют удельной электрической проводимостью. Он зависит от материала проводника и при данной температуре является постоянной величиной.

Преобразуем выражение (2.8). Так как J = I/S, E = U/I, a ( — удельное сопротивление), то 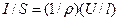, откуда

.

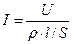Введя понятие сопротивления проводника через соотношения ρl/S = R (R - сопротивление проводника), окончательно получим

(2.9)

Выражение (2.9) является законом Ома для участка цепи: сила тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку.

Приведенные рассуждения справедливы при условии, что γ, а следовательно, и R - постоянные величины, т. е. для линейной цепи, характеризуемой зависимостью , ток линейно зависит от напряжения. Отсюда следует важный вывод: закон Ома справедлив для линейных цепей (R = const).

Рассмотрим полную цепь (рис. 2.3). Согласно закону Ома для участка цепи, U=IR, U_BT=IR_BT. Тогда в соответствии с (2.6) E = IR-\- IR_ВТ. Отсюда

(2.10)

Выражение (2.10) является законом Ома для всей цепи: сила тока в цепи прямо пропорциональна ЭДС источника.

Из выражения 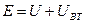следует, что , т. е. при наличии тока в цепи напряжение на ее зажимах меньше ЭДС источника на значение падения напряжения на внутреннем сопротивлении источника.