 |
|
Момент инерции, теорема Штейнера
Моментом инерции I материальной точки относительно оси называют произведение массы этой точки m на квадрат ее расстояния r до оси
.
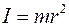Моментом инерции I системы n материальных точек относительно оси называют сумму моментов инерции материальных точек системы
 .
|
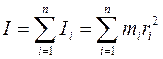Представляя тело состоящим из сколько угодно малых частей объемом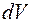 
и массы 
, его момент инерции можно рассчитать как
 ,
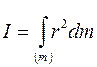| (1) |
где r – расстояние от элемента тела объемом 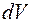до оси, относительно которой рассчитывается момент инерции.
Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.
Так как 
, где r – плотность тела в данной области 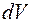, то формулу (2) можно записать в виде
.
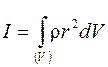Если тело однородно, т.е. 
, то
.
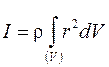Наиболее просто определяются моменты инерции тел правильной геометрической формы с равномерным распределением массы по объему. Для примера найдем момент инерции сплошного однородного цилиндра (диска) массой m и радиусом R относительно оси симметрии. Для этого тело мысленно разбиваем на тонкие концентрические слои толщиной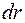 
(рис. 6), частицы которых находятся на одинаковом расстоянии от оси.
|
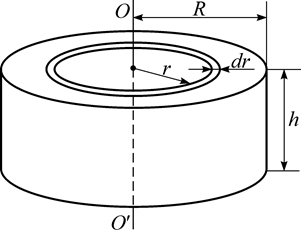
| Рис. 6. Разбиение цилиндра |
Пусть радиус некоторого слоя r, тогда масса частиц, заключенных в этом слое, будет равна
,
где h – высота цилиндра, 
– плотность вещества цилиндра.
Все частицы слоя будут находиться на расстоянии r от оси, следовательно, момент инерции этого слоя будет
.
Момент инерции всего цилиндра
.
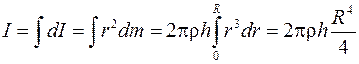Поскольку масса цилиндра 
, то получим, что момент инерции равен
 .
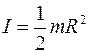| (2) |
Из (2) следует, что момент инерции сплошного однородного цилиндра зависит только от его массы и радиуса и не зависит от высоты. Поэтому формула (2) применима для расчета момента инерции сплошного однородного диска относительно оси симметрии.
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции тела относительно любой параллельной оси можно определить, воспользовавшись теоремой Штейнера:
момент инерции I тела относительно произвольной оси равен сумме момента инерции тела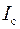 
относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния а между осями
 .
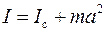| (3) |
Момент инерции тела относительно оси является мерой инертности тела при вращательном движении (мерой инертности тела при поступательном движении является масса) и зависит не только от массы тела, но и от ее распределения в пространстве относительно оси. Тело обладает определенным моментом инерции относительно любой оси независимо от того, вращается оно или находится в покое.