 |
|
Метод трифилярного подвеса
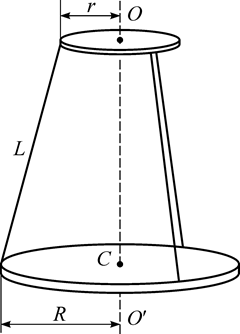
В настоящей работе моменты инерции твердых тел определяются с помощью трифилярного подвеса, представляющего собой диск радиуса R, подвешенный горизонтально на трех нитях длиной L к неподвижному диску меньшего радиуса r (рис. 7).
Центры дисков расположены на одной вертикальной оси 
, вокруг которой нижний диск может совершать крутильные колебания. При колебаниях центр масс С диска радиуса R перемещается вдоль оси .
|
| Рис. 7. Трифилярный подвес |
При повороте нижнего диска на угол j вокруг оси его перемещение равно h (рис. 8), а приращение потенциальной энергии
,
где m – масса нижнего диска.
|
| Рис. 8. Трифилярный подвес при повороте на угол φ0 |
В процессе крутильных колебаний, нижний диск совершает поступательное и вращательное движение, поэтому его полная кинетическая энергия складывается из кинетической энергии поступательного движения и кинетической энергии вращательного движения, т.е.
,
где I – момент инерции диска относительно оси , w – угловая скорость диска,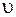 
– скорость центра масс диска.
При небольших смещениях диска по вертикали по сравнению с длиной нитей (при малых углах поворота), пренебрегая вязкостью воздуха, можно показать, что диск совершает гармонические колебания и угол j его поворота изменяется со временем по гармоническому закону
,
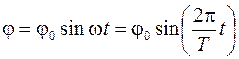где 
– амплитуда углового смещения, T – период колебаний диска.
Изменение потенциальной энергии диска при максимальном угле поворота равно максимальной кинетической энергии вращательного движения, которой обладает диск в момент прохождения положения равновесия, т.е.
,
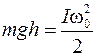где 
– угловая скорость диска в момент прохождения положения равновесия.
Из последнего равенства следует момент инерции диска
 .
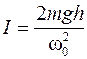| (4) |
Поскольку угловая скорость диска меняется по гармоническому закону
,
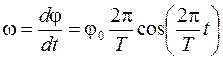то, максимальная угловая скорость равна
 .
| (5) |
Высоту h, на которую поднимается диск, можно определить из геометрических соображений (рис. 8)
 .
| (6) |
Но
 ,
 .
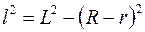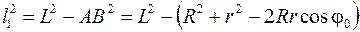| (7) (8) |
С учетом соотношений (7), (8) равенство (6) можно записать в виде
.
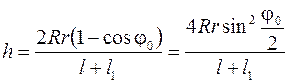При малых углах можно считать, что 
, а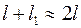 
. Таким образом
 .
| (9) |
Подставляя (5), (7), (9) в (4) и заменяя в формуле радиусы дисков на диаметры, получим
 .
| (10) |
Формулу (10) можно применять не только для расчета момента инерции 
диска относительно оси , но и для расчета момента инерции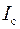 
диска с грузами. Тогда момент инерции 
груза можно найти
 ,
| (11) |